四次贝塞尔
今天考试怎么都算不对,好烦,下午写了个玩(也不懂对不对)
真是可怕的一天
先上公式
p
(
t
)
=
[
t
4
t
3
t
2
t
1
]
[
1
−
4
6
−
4
1
−
4
12
−
12
4
0
6
−
12
6
0
0
−
4
4
0
0
0
1
0
0
0
0
]
[
p
1
p
2
p
3
p
4
p
5
]
p(t)=\begin{bmatrix}t^4&t^3&t^2&t&1\end{bmatrix} \begin{bmatrix} 1&-4&6&-4&1\\ -4&12&-12&4&0\\ 6&-12&6&0&0\\ -4&4&0&0&0\\ 1&0&0&0&0 \end{bmatrix} \begin{bmatrix}p_1\\ p_2\\ p_3\\ p_4\\ p_5\end{bmatrix}
p(t)=[t4t3t2t1]⎣⎢⎢⎢⎢⎡1−46−41−412−12406−12600−4400010000⎦⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎡p1p2p3p4p5⎦⎥⎥⎥⎥⎤
把t从0到一套,线条就出来了。
代码
工具:vs2019
库:EasyX,Eigen
关于Eigen库怎么导到vs:
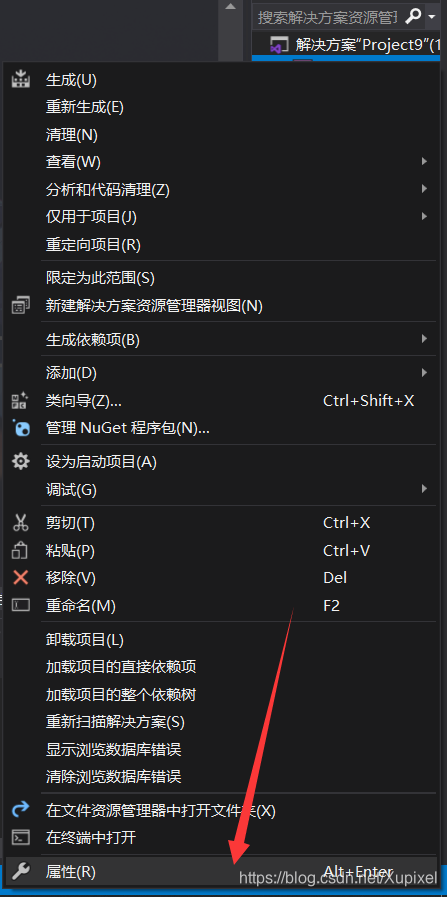
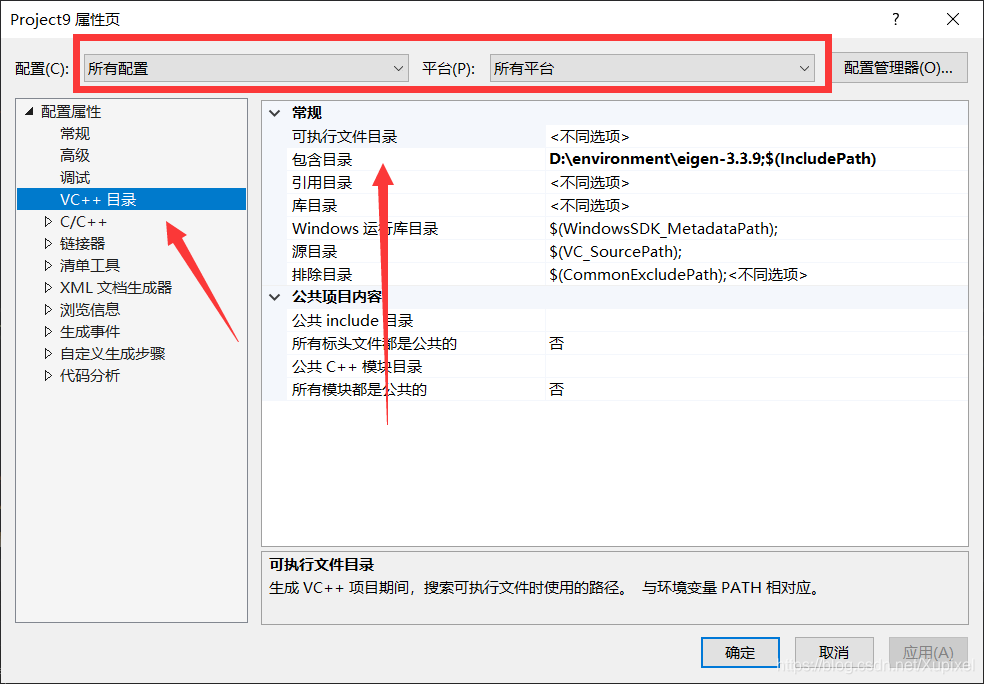
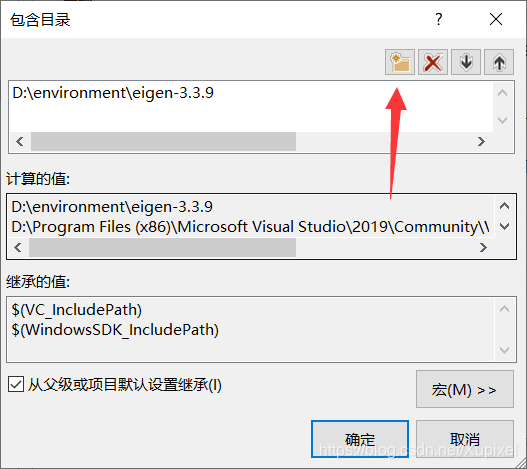
将eigen的路径添加就可以了。
//手动实现四阶贝塞尔
#include <graphics.h>
#include <conio.h>
#include <vector>
#include<Eigen/core>
#include<Eigen/Dense>
using namespace Eigen;
using namespace std;
POINT pts[] = { {0,0},{100,100},{200,200},{300,300},{400,400} };
int j = -1, i;
void my_bezier(POINT pts[]) {
Matrix<double, 5, 5> M;
M << 1, -4, 6, -4, 1,
-4, 12, -12, 4, 0,
6, -12, 6, 0, 0,
-4, 4, 0, 0, 0,
1, 0, 0, 0, 0;
Matrix<double, 5, 2> B;
for (int i = 0; i < 5; i++) {
B(i, 0) = (double)pts[i].x;
B(i, 1) = (double)pts[i].y;
}
Matrix<double, 5, 2> MB = M * B;
Matrix<double, 1, 2> pre_p;
pre_p << pts[0].x, pts[0].y;
for (int i = 1; i <= 200; i++) {
double t = i / 200.0;
Matrix<double, 1, 5> T;
T << pow(t, 4), pow(t, 3), pow(t, 2), t, 1;
Matrix<double, 1, 2> p = T * MB;
line(pre_p(0, 0), pre_p(0, 1), p(0, 0), p(0, 1));
pre_p = p;
}
}
void paint() {
setcolor(DARKGRAY);
polyline(pts, 5);
setcolor(WHITE);
my_bezier(pts);
for (i = 0; i < 5; i++) {
circle(pts[i].x, pts[i].y, 10);
}
}
int main() {
initgraph(640, 480); // 初始化图形窗口
paint();
MOUSEMSG m;
while (1) {
m = GetMouseMsg();
BeginBatchDraw();
switch (m.uMsg) {
case WM_LBUTTONDOWN:
for (i = 0; i < 5; i++) {
if (abs(m.x - pts[i].x) < 10 && abs(m.y - pts[i].y) < 10)j = i;
}
case WM_MOUSEMOVE:
if (j > -1) {
pts[j] = { m.x,m.y };
cleardevice();
paint();
}
break;
case WM_LBUTTONUP:
j = -1;
break;
}
EndBatchDraw();
}
_getch(); // 按任意键退出
closegraph();
return 0;
}
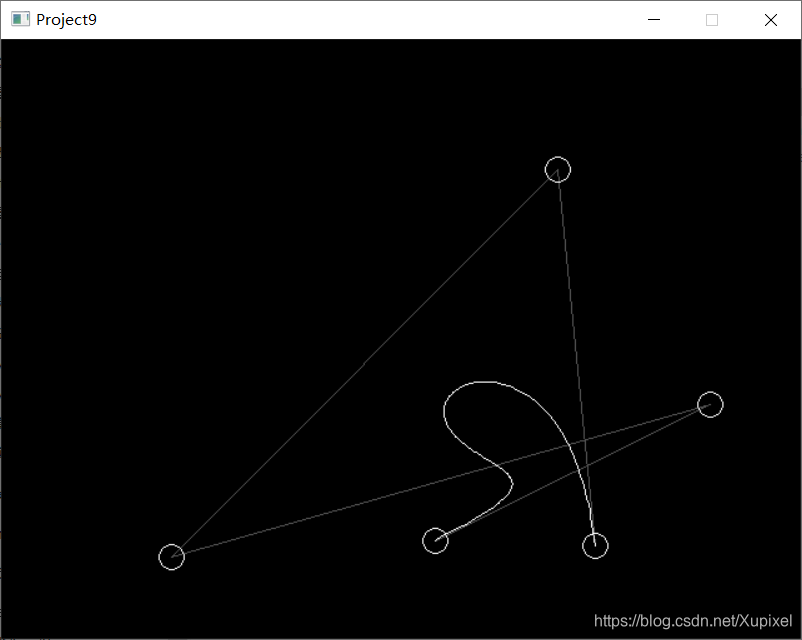







 本文详细介绍了如何使用四次贝塞尔公式在计算机图形中生成平滑路径,并通过Visual Studio和Eigen库的实例,展示了如何在C++中实现贝塞尔曲线的编程实现。通过一步步教学,适合初学者理解并掌握贝塞尔曲线在图形编程中的应用。
本文详细介绍了如何使用四次贝塞尔公式在计算机图形中生成平滑路径,并通过Visual Studio和Eigen库的实例,展示了如何在C++中实现贝塞尔曲线的编程实现。通过一步步教学,适合初学者理解并掌握贝塞尔曲线在图形编程中的应用。
















 1838
1838

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








