链表:
-
无需事先估计空间
-
增删不需要挪动元素,比较方便
-
不支持随机访问
-
地址不连续
-
时间复杂度指的是一个数量级的概念(查找第i个也是O(n))
-
链式存储时,结点的存储地址可以随意分配(链表中有指针域可以找到下一个链表结点的存储地址,连续与否都可以)
-
链表是一种物理存储单元上非连续、非顺序的存储结构
-
线性表的顺序存储结构中逻辑顺序与物理顺序总是一致的,但链表存储结构不一致
-
数组从栈中分配空间(数组元素在栈区),链表从堆中分配空间(在堆区)
数组静态分配内存,链表动态分配内存
数组在内存中连续,链表不连续
有序数组利用下标定位时间复杂度为O(1),链表定位元素的时间复杂度为O(n)
有序 数组插入删除元素的时间复杂度为O(n), 链表插入删除元素的时间复杂度为O(1)
建立一个n个节点的单链表的时间复杂度为O(n) -
循环链表中尾指针指向终端节点(开始节点:(rear->next)->next / 终端结点 rear)
-
线性表的顺序存储结构的地址是连续的,所以可以通过计算地址来随机存取(直接访问),而链式存储结构的存储地址不是连续的,所以只能通过结点的指针顺序存取()
-
单链表 删除/查找时间复杂度 O(1),查找的时间复杂度O(n)
-
二分查找法只适合顺序存储结构
-
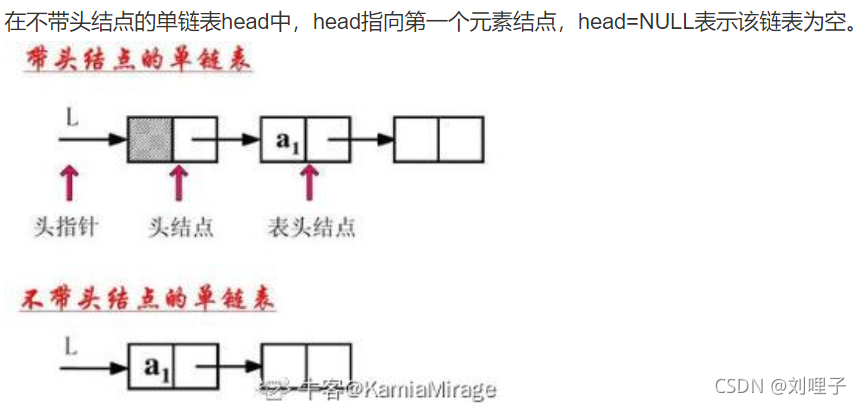
-
单链表的存储密度<1,(存储密度=单链表的数据项所占空间 / 结点所占空间)
-
单链表的插入与删除不需要移动元素,需要移动指针
栈/队列




- 递归的过程就是栈保存现场地址的过程(数据入栈、运算、出栈、返回结果)
- 栈与队列顺序存储/链式存储的插入与删除都在一段进行,时间复杂度为O(1)
- 进栈n个数据,出栈的序列的种类数:
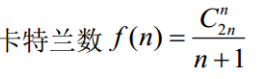
树:
-
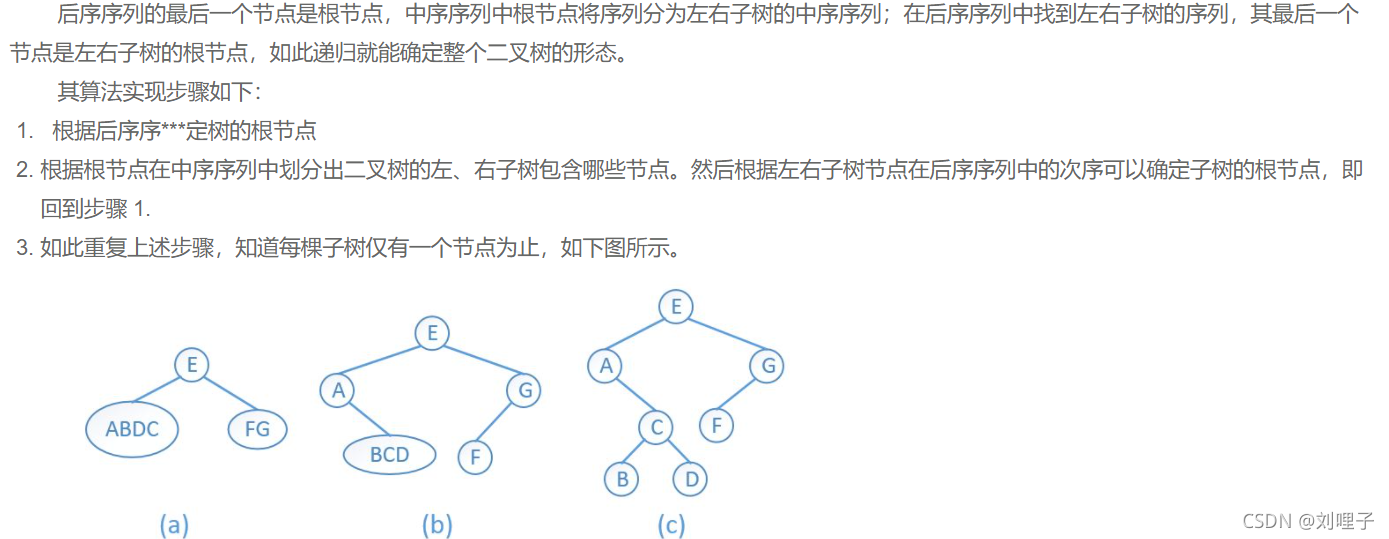
中序遍历+后序遍历——二叉树
-
在树中,叶子节点的个数比度为2的节点数多1(+1)
-
由树转换为二叉树,这个二叉树的形态唯一
-
任何树中,分支数(在二叉树中叫度之和)比结点数少一
-
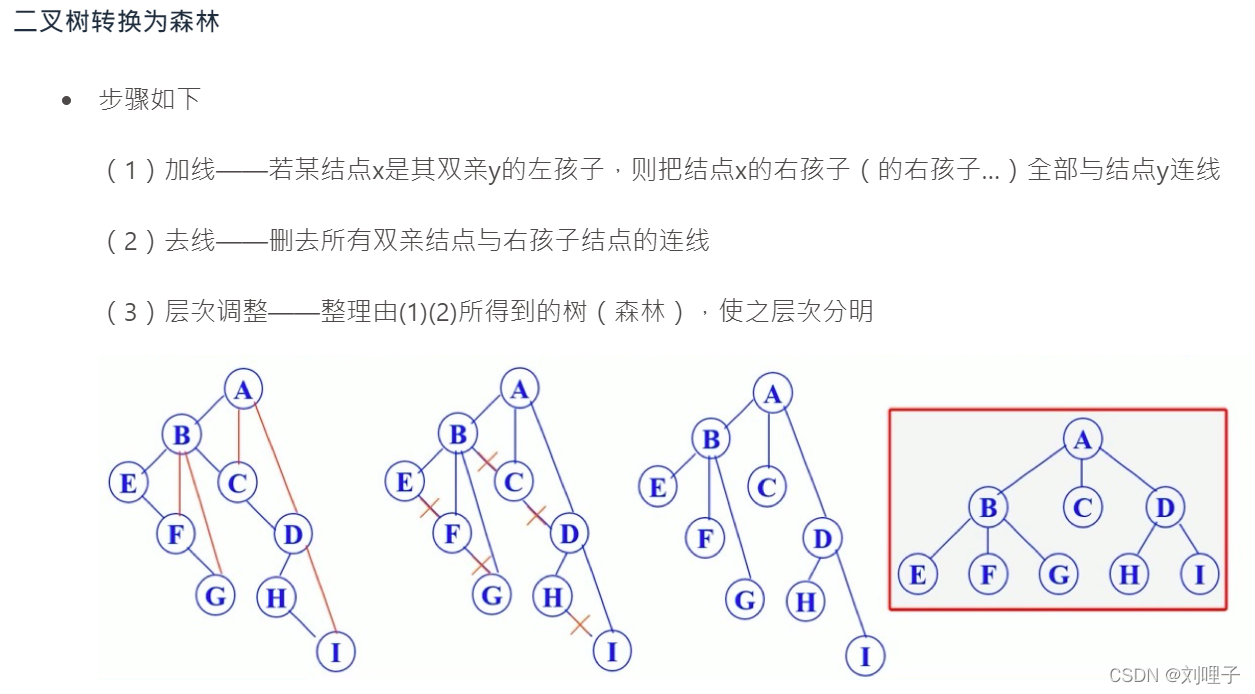
图:
-
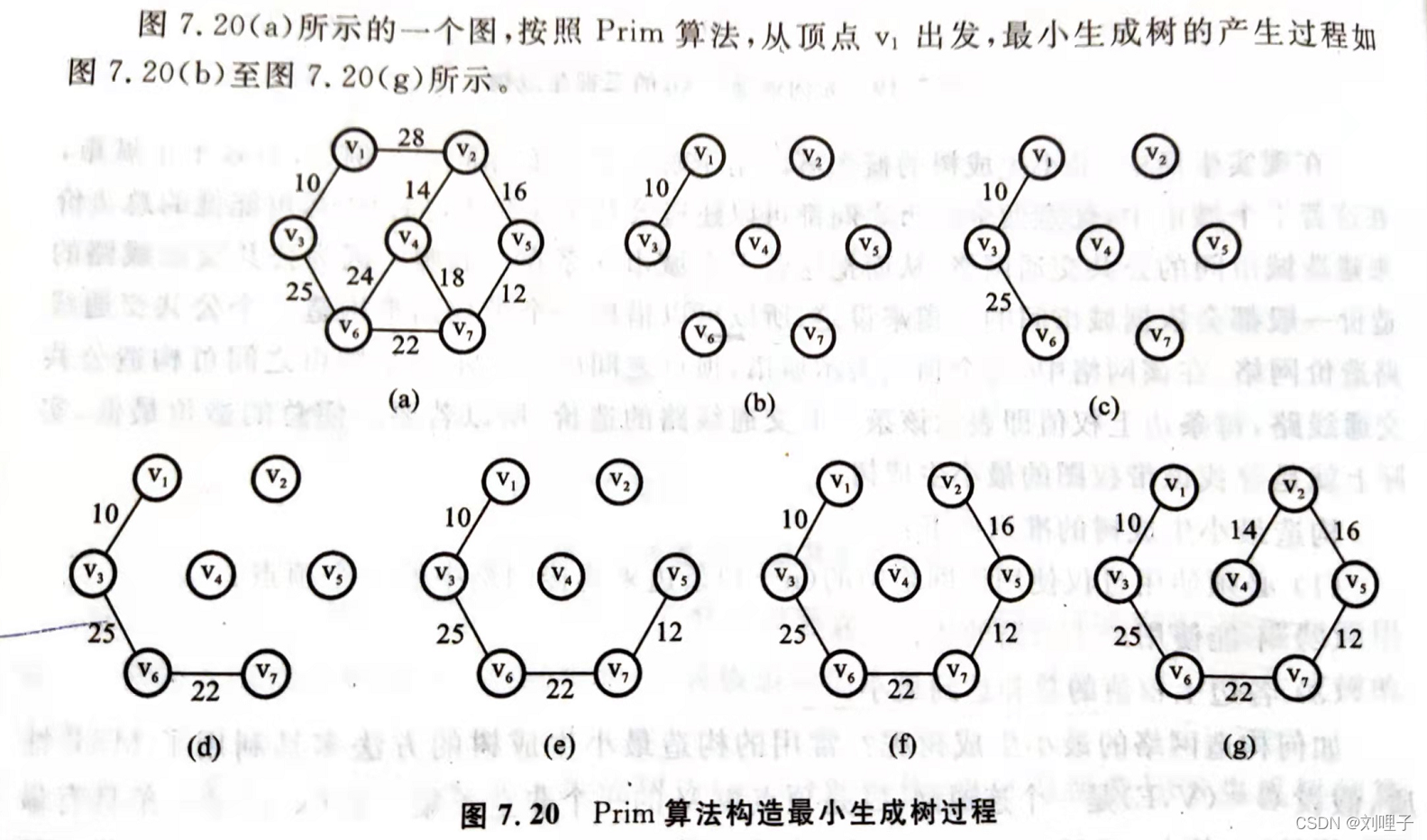
最小生成树 :a.必须使用(n-1)条边来构造n个顶点 b.不能使用回路的边 c.权值最小
(1)Prim算法:
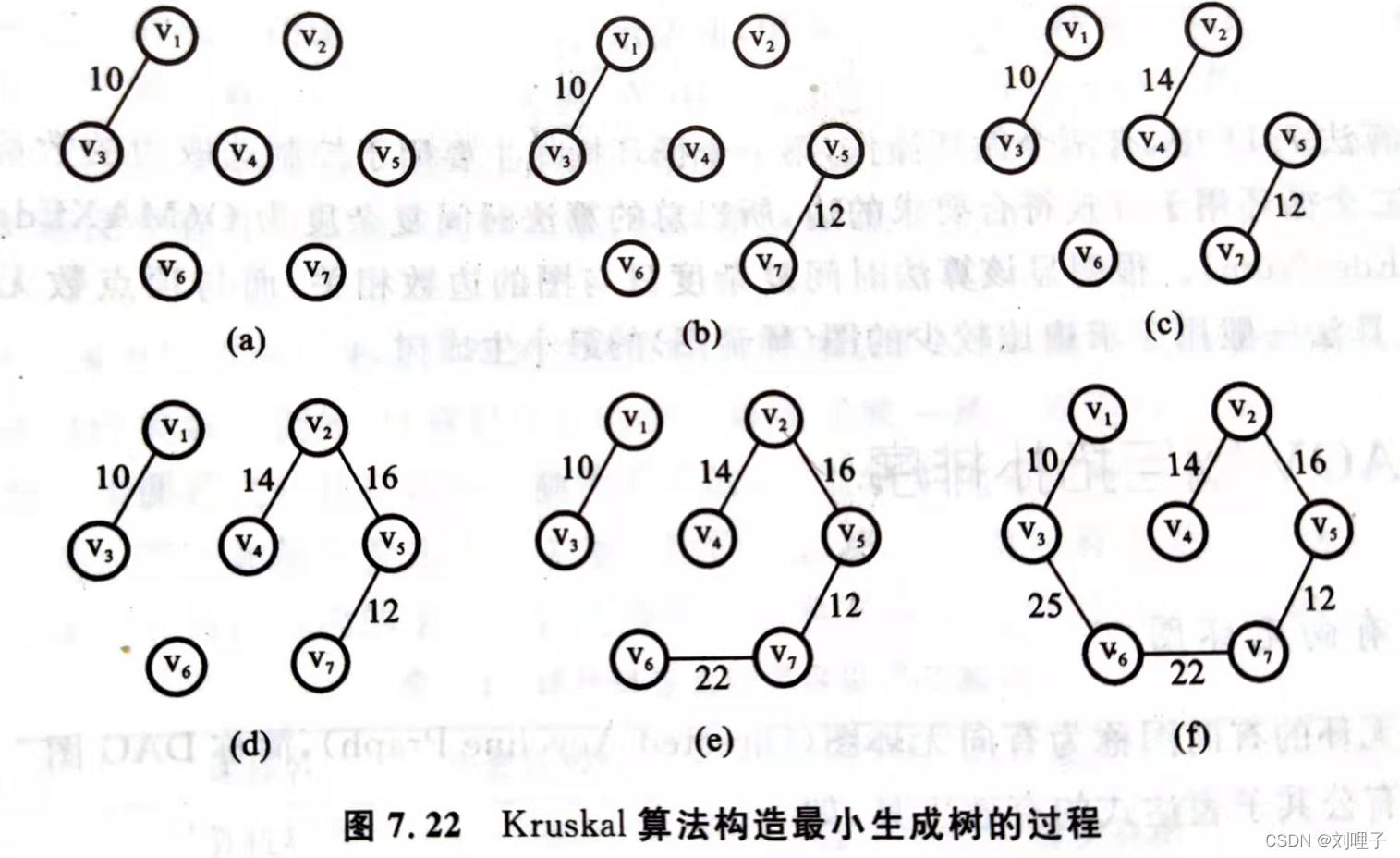
(2)Kruskal算法
-
AOV网:无权有向图-拓扑排序
AOE网:有权有向图-关键路径(最长的路径) -
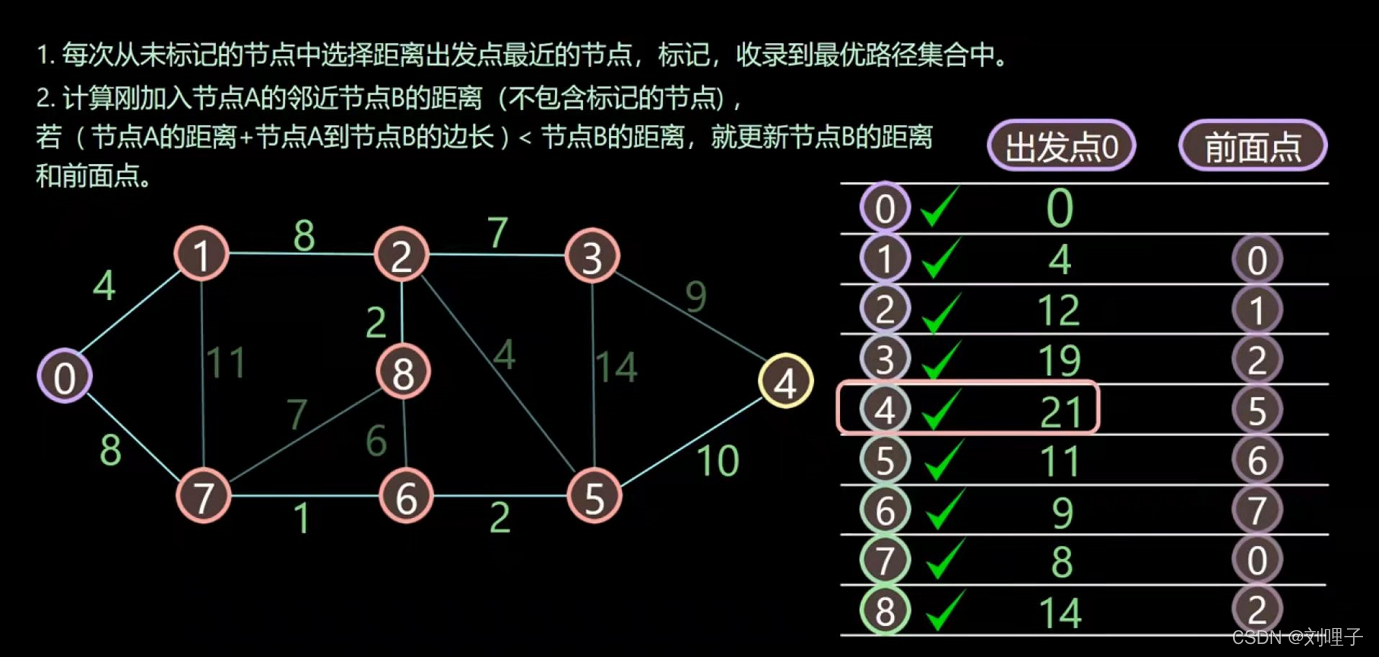
最短路径-Dijkstra算法
-
度数之和=2*边数————所以无向图的度数之和一定是偶数
-
BSF和DSF算法一次遍历完整个图的所有元素条件必须是连通图(非连通图不可以)
-
保证n个顶点无向图在任何情况下都是连通的所需边数最少是:(n-1)(n-2)/2+1 <保证(n-1)顶点图是完全图 >
-
图中任意两点度的和大于或等于顶点总数,那一定是哈密尔顿图
-
建立邻接表或逆邻接表时,若顶点信息即为编号,则时间复杂度为O(n+e)。
若需要通过查找才可以得到位置,则为O(n*e) -
n个顶点的强连通图最多有n(n-1)条边,最少有n条边
-
有向图邻接表某顶点链表长度为0其度数不一定为0(度=出度+入度)
-
B-树只支持随机搜索,B+树支持随机和顺序搜索(优势在于叶子结点之间有指针)
-
邻接表得节点数等于=结点数+边数
-
有向图-出度=入度
-

查找:
- 二叉排序树的插入元素一定称为叶子结点,AVL树(平衡二叉树)插入元素时要做出调整
- 哈希表查找元素是最快的,时间复杂度为O(1)
- 折半查找法的时间复杂度为O(log 2 N)
其他:
-
list为双向链表,支持快速增删
-
vector为数组,支持快速随机访问,插入删除时需要移动其他元素,复杂度高
-
map、set:为红黑树,插入删除复杂度低
-
堆(内存)与栈(内存)之间的区别:
a·堆:堆的内存由程序员来分配,且在使用中容易产生碎片 (自己做菜自己吃,什么时候收盘子自己知道,但是可能会浪费(产生碎片),因为可能自己一个人吃不完。)
b· 桟:栈的内存由系统来自动分配,但自由度小 (公司食堂,你吃饭由食堂工作人员帮你打饭和分配位置,吃完了工作人员帮你收盘子。你浪费粮食(碎片)那是不可能的,因为食堂会把碎片拿去喂猪。) -
局部变量分布在栈上,new出来的对象分布在堆上
-
c语言中标识符只能以字母和下划线为开头
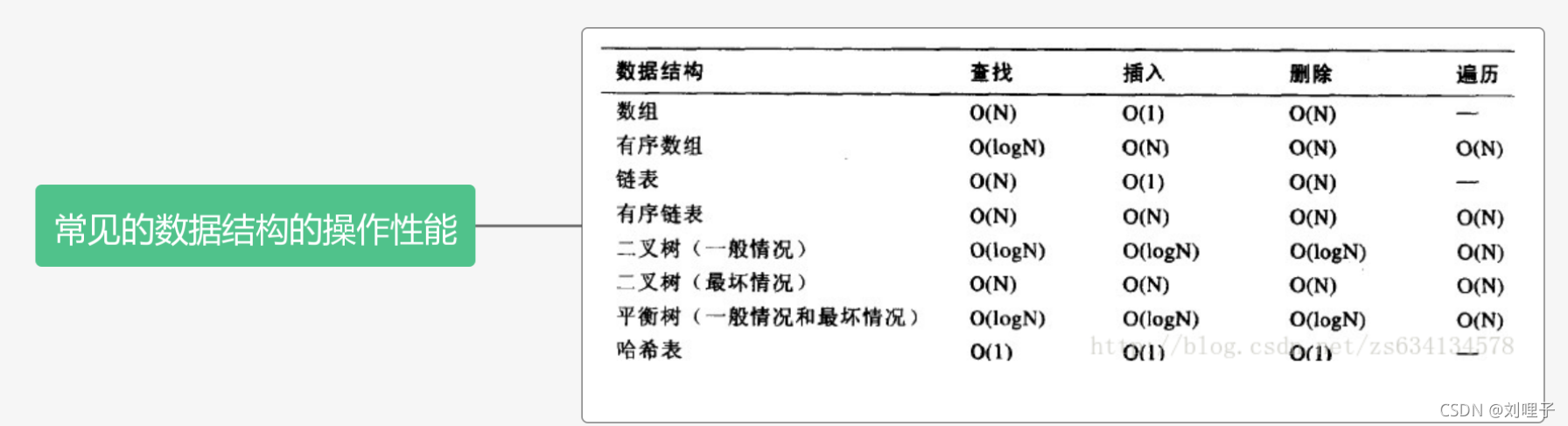
- 查二维数组的时间复杂度是O(1)
基础知识
- 数据结构:是指互相之间存在着一种或多种关系的数据元素的集合
- 算法:对特定问题求解步骤的一种描述,是指令的有限序列
- 算法五特征:有穷性、确定性、可行性、输入、输出
- 好的算法要求:正确、可读、健壮、高效
- 数据逻辑结构包括:集合结构、线性结构、树状结构、图形结构
- 数据存储结构包括:顺序存储、链式存储、索引存储、散列存储。
- 树形结构和图形结构合称为:非线性结构



算法
- 链表的删除
- 链表的添加
- 链表的遍历
- 双向链表的删除
- 尾递归
- 三元组储存
- 二叉树的储存(双亲、孩子)





 本文深入探讨了数据结构中的链表特性,包括增删便利性、非连续存储和时间复杂度。同时,介绍了树与图的相关概念,如二叉树、最小生成树算法以及图的遍历。还涵盖了查找算法,如二叉排序树、哈希表和折半查找。此外,讨论了栈和队列在递归和存储过程中的作用,并对比了数组和链表的优缺点。
本文深入探讨了数据结构中的链表特性,包括增删便利性、非连续存储和时间复杂度。同时,介绍了树与图的相关概念,如二叉树、最小生成树算法以及图的遍历。还涵盖了查找算法,如二叉排序树、哈希表和折半查找。此外,讨论了栈和队列在递归和存储过程中的作用,并对比了数组和链表的优缺点。

















 6215
6215

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








