CS224d lecture10 GRU与NMT相关_重置门和更新门是向量吗-优快云博客

本文链接：https://blog.youkuaiyun.com/Xiao_yanling/article/details/94429519

本文深入探讨了门控循环单元（GRU）的工作原理，包括其如何通过更新门和重置门解决传统循环神经网络的梯度消失问题，以及与长短期记忆单元（LSTM）的对比分析。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1.GRUs

在时间t处看到的词如何影响后面的n个词（即t+n处看到的）？
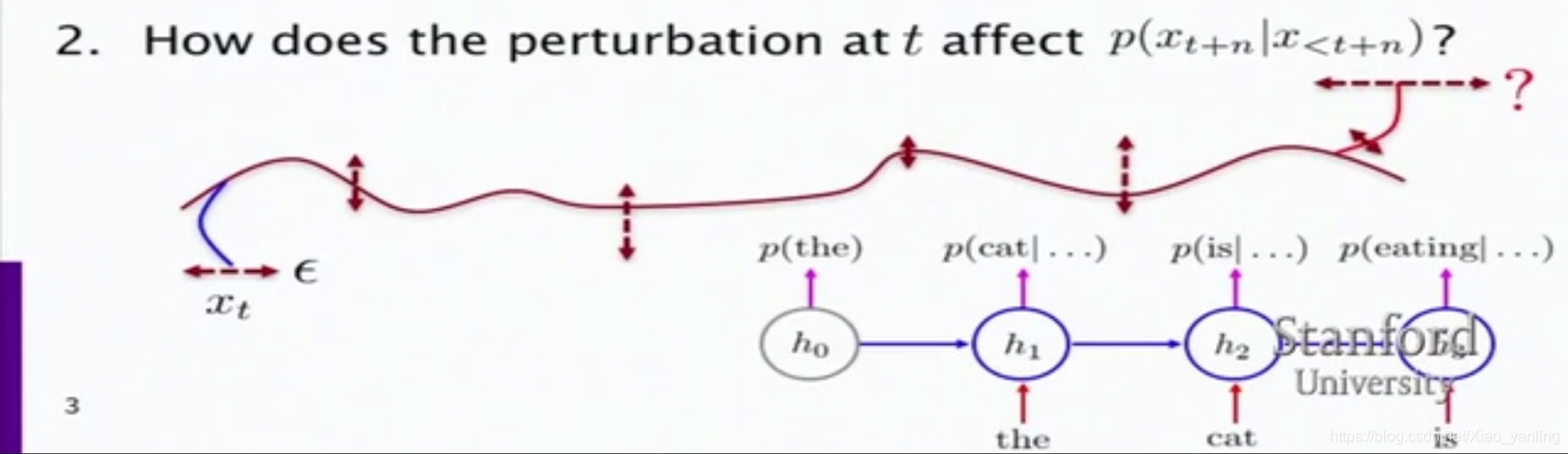
在这里插入图片描述
反向传播中连续的矩阵乘法可能会造成梯度消失。下图是基本的循环神经网络中在时间序列上的传递过程。

在门控单元的情况下，除了传统循环神经网络在时间序列上的连接，还会有其余短连接，如下图绿圈表示的连接，能够实现t时间直接影响t+x，在反向传播时就能计算t时间段对t+x时间段的影响，以此学习到长期的依赖关系。
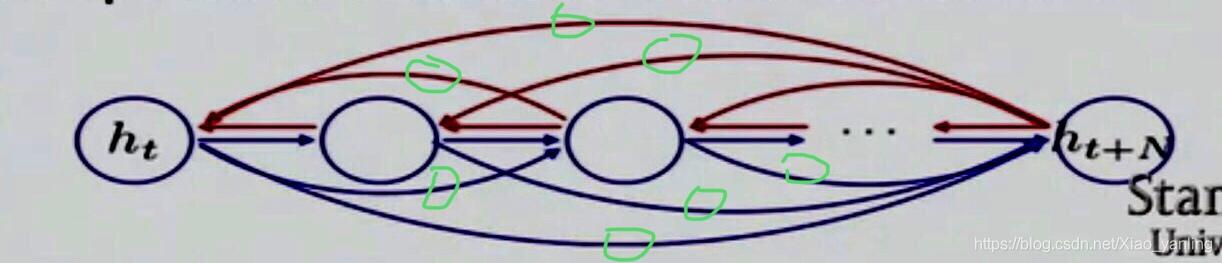
在这里插入图片描述
GRU具体实现：
$f(ht−1.xt)=ut⊙ht~+(1−ut)⊙ht−1f(h_{t-1}.x_t)=u_t\odot{\widetilde{h_t}}+(1-u_t)\odot{h_{t-1}}$
$ht~=tanh(W[xt]+U(rt⊙ht−1+b)\widetilde{h_t}=tanh(W[x_t]+U(r_t\odot{h_{t-1}}+b)$
更新门：
$rt=σ(Wr[xt]+Urht−1+br)r_t=\sigma(W_r[x_t]+U_rh_{t-1}+b_r)$

重置门：
$ut=σ(Wu[xt]+Uuht−1+bu)u_t=\sigma(W_u[x_t]+U_uh_{t-1}+b_u)$

更新门和重置门都是向量

带有门控单元的RNN神经网络计算过程总结：
首先重置门能学到一个想要读取和使用的隐藏层的子集，读取子集后( $rt⊙ht−1r_t\odot{h_{t-1}}$ )进行标准的RNN计算去更新内容（即上述表达式中的 $ht~=tanh(W[xt]+U(rt⊙ht−1+b)\widetilde{h_t}=tanh(W[x_t]+U(r_t\odot{h_{t-1}}+b)$ ），然后选择可写入的隐藏层子集（更新门），更新写回（即 $h←u⊙h~+(1−ut)⊙hh\leftarrow{u\odot{\widetilde{h}+(1-u_t)\odot{h}}}$ ）。

GRU不会有梯度消失问题原因：
$f(ht−1.xt)=ut⊙ht~+(1−ut)⊙ht−1f(h_{t-1}.x_t)=u_t\odot{\widetilde{h_t}}+(1-u_t)\odot{h_{t-1}}$ 式子中+是一个线性关系，当 $u_t$ 趋近于0时，相当于直线逼近与 $h_t$ ,不会有任何信息的损失，可以有很长的距离依赖，不用每次都乘以矩阵（造成梯度消失），当 $u_t$ 趋近于1，没有任何信息从 $h_{t-1}$ 流出，没有长距离的依赖，就是模型当前学到的东西。

GRU与LSTM对比：
在这里插入图片描述
GRU的h等价于LSTM的c，LSTM有一个遗忘门（f）和一个输入门（i）。
GRU中有重置门，在计算候选更新时（ $h~\widetilde{h}$ ）可能忽略部分过去的值；LSTM在候选更新时（ $c~\widetilde{c}$ ）总是使用当前输入（ $c~=tanh(Wc[xt]+Ucht−1+bc\widetilde{c}=tanh(W_c[x_t]+U_ch_{t-1}+b_c$ ，其中 $h_{t-1}$ 由 $c_{t-1}$ 计算而来(即 $ht=ot⊙tanh(ct)h_t=o_t\odot{tanh(c_t)}$ )）。