机器学习之Logistic回归

1.Logistic回归简介

线性回归能够找到一个假设函数来估计原函数，从而根据特征变量来得到假设值，但线性回归模型不能达到分类的效果。在线性回归的基础上，我们将假设值和概率结合得到分类器，达到分类的效果。虽然Logistic回归是回归模型，但在实际项目中我们经常用于分类问题。

2.Sigmoid函数

为什么选择Sigmoid函数呢？我们目标是寻找函数进行分类，首先假设任意多类的分类问题（不仅是两类）。Exponential假设第i个体征对第k类问题的贡献是$w_{ki}$，则数据点$(x_1,x_2,\dots ,x_n)$属于第k类的概率正比于
$$exp(w_{k1}{x}_1+\dots +w_{kn}{x}_n)。$$
因为一个数据点属于各类的概率之和为1，所以可以得到
$$P(y=k)=\frac{exp({\sum }_{i=1}^n{w}_{ki}{x}_i)}{{\sum }_{k^{\prime }}exp({\sum }_{i=1}^n{w}_{k^{\prime }i}{x}_i)}$$
现在回到两类（0,1）的情况，此时分母上只有两项
$$P(y=1)=\frac{exp({\sum }_{i=1}^n{w}_{1i}{x}_i)}{exp({\sum }_{i=1}^n{w}_{1i}{x}_i)+exp({\sum }_{i=1}^n{w}_{0i}{x}_i)}$$
公式分子、分母同时除以分子，并设$w_i=w_{1i}-w_{0i}$，则有
$$P(y=1)=\frac{1}{1+exp(-{\sum }_{i=1}^n{w}_i{x}_i)}$$
上述公式便是Logistic函数，参数$w_i$表示第i个特征对1类的贡献与0类的贡献的差值。
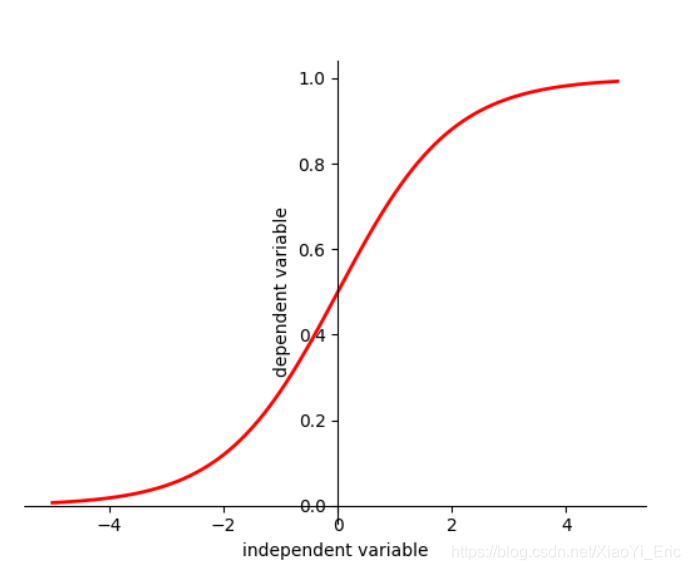
$$SigmoidFunction:f(x)=\frac{1}{1+e^{-x}}$$
Sigmoid函数具有如下性质

• 函数连续且单调递增
• 函数关于（0,0.5）对称
• $x\in (-\infty ,\infty )$时$y\in (0,1)$

#plot sigmoid function 
import numpy as np
import matplotlib.pyplot as plt

##sigmoid function
x=np.arange(-5,5,0.1)
y=1/(1+np.exp(-x))

#plot
plt.figure()
plt.plot(x,y,color='red',linewidth='2')
ax=plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
plt.xlabel('independent variable')
plt.ylabel('dependent variable')
plt.show()

3.Logistic回归推导

• 特征向量$X=(x_0,x_1,x_2\dots x_n)$，默认$x_0=1$。
• $\theta =({\theta }_0,{\theta }_1,{\theta }_2\dots {\theta }_n)$
• $n$表示特征数量
• $m$表示训练数据数量

线性回归函数为$z={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+\dots +{\theta }_n{x}_n={\theta }^{T}X$。对于Logistic回归来说，其思想也基于线性回归（Logistic回归属于广义线性回归模型）。结合线性回归和Sigmoid函数，将线性回归得到的结果映射到Sigmoid函数之中，我们便得到目标函数。
$$h(X)=\frac{1}{1+e^{-{\theta }^{T}X}}$$
我们可以把$h(X)$看成样本数据的概率密度函数，当$h(X)<0.5$是判断当前数据属于A类，当$h(X)>0.5$判断当前数据属于B类。对于上述函数$h(X)$，接下来我们需要做的便是怎样去估计参数$\theta$。

条件概率$P(y=1|X)$为某事件发生的概率，Logistic回归模型可以表示为
$$P(y=1|X)=\pi (X)=\frac{1}{1+e^{-{\theta }^{T}X}}$$
条件概率$P(y=0|X)$为某事件不发生的概率，Logistic回归模型可以表示为
$$P(y=0|X)=1-\pi (X)=\frac{1}{1+e^{{\theta }^{T}X}}$$
因此我们可以得到事件的发生比为
$$odds=\frac{P(y=1|X)}{P(y=0|X)}$$
事件的发生和不发生为相互独立事件，样本数据结果记录为$(y_1,y_2\dots y_m)$。设$p_i=P(y_i=1|X_i)$为给定条件下得到$y_i=1$的概率，同样$1-p_i=P(y_i=0|X_i)$的概率，所以得到一个观测值的概率为$P(y_i)=p_i^{y_i}(1-p_i{)}^{1-y_i}$，最后参数估计时我们可以采用极大似然估计。

各个观测样本之间相互独立，那么它们的联合分布为各边缘分布的乘积，得到如下极大似然函数
$$L(\theta )=\prod _{i=1}^m[\pi (X_i){]}^{y_i}[1-\pi (X_i){]}^{1-y_i}$$
目标便是求得使这一似然函数值最大的参数估计，于是函数取对数得到
lnL(θ)=∑i=1m{yiln[π(Xi)]+(1−yi)ln[1−π(Xi)]} lnL(\theta)=\sum_{i=1}^{m}\left \{ y_iln[\pi(X_i)] +(1-y_i)ln[1-\pi(X_i)] \right \} lnL(θ)=i=1∑m​{yi​ln[π(Xi​)]+(1−yi​)ln[1−π(Xi​)]}

$$=\sum _{i=1}^{m}ln[1-\pi (X_i)]+\sum _{i=1}^m{y}_{i}ln\frac{\pi (X_i)}{1-\pi (X_i)}$$

$$=\sum _{i=1}^{m}ln[1-\pi (X_i)]+\sum _{i=1}^m{y}_i{\theta }^{T}X$$

$$=\sum _{i=1}^m-ln[1+e^{{\theta }^{T}x}]+\sum _{i=1}^m{y}_i{\theta }^{T}X$$

通过上面得到的结论来求解使得似然函数最大化的参数向量，此处我们利用梯度下降算法求$\theta$。首先在前面乘上负的系数$-\frac{1}{m}$，所以$J(\theta )$最小时的$\theta$为最佳参数。
$$J(\theta )=-\frac{1}{m}lnL(\theta )$$

$$=-\frac{1}{m}\left\{\sum _{i=1}^m-ln[1+e^{{\theta }^{T}x}]+\sum _{i=1}^m{y}_i{\theta }^{T}X\right\}$$

4.梯度下降算法

4.1梯度下降算法简述

实际生活中我们有时也利用梯度下降算法，比如我们处在一座山的某处位置，但我们并不知道如何下山，于是决定走一步算一步，但每次都沿着最陡峭的地点下山，也就是沿着梯度的负方向前进。但有事也会遇见问题，不能每次都到达山脚，可能到达山峰的某个局部最低点。

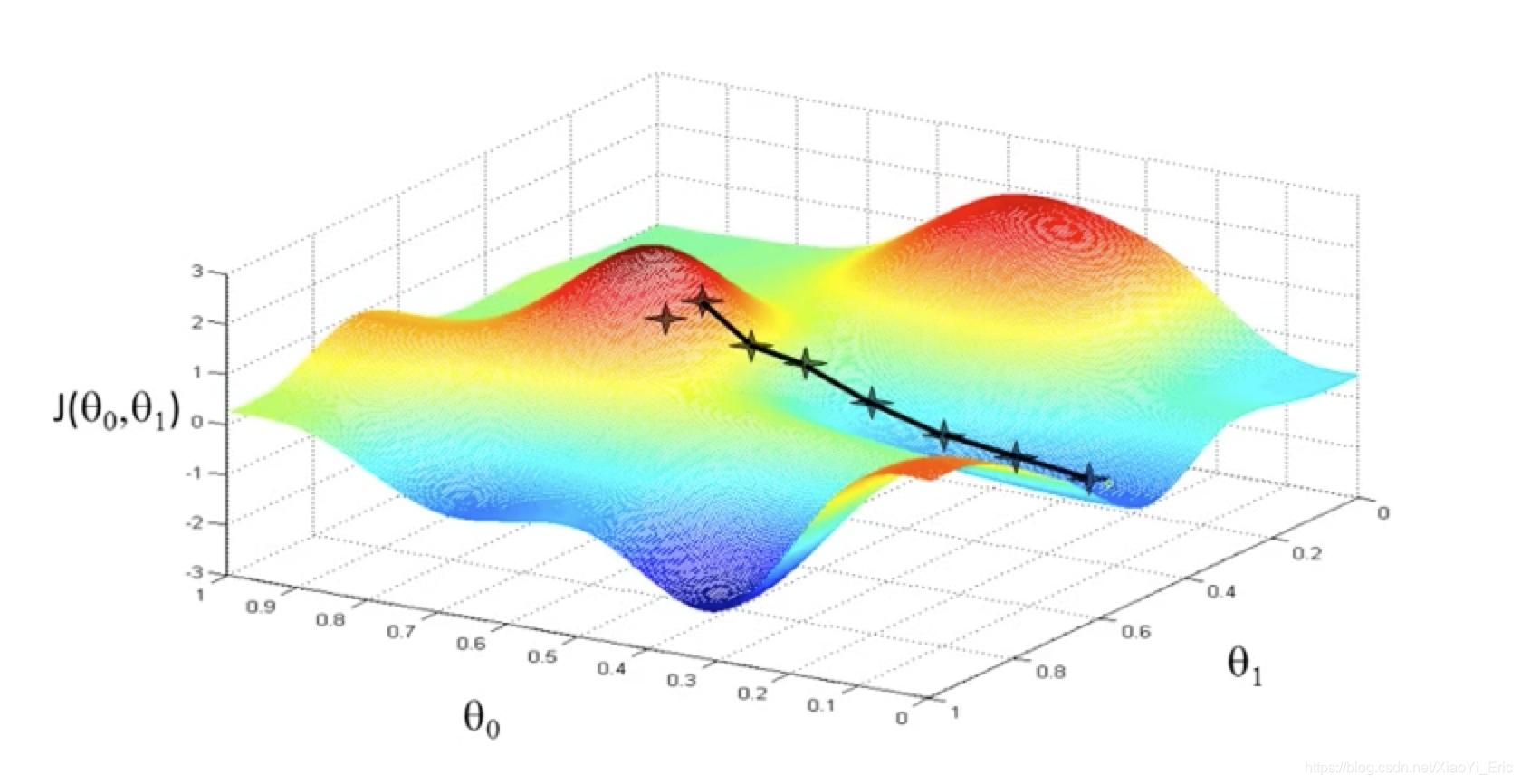
从上面解释可以看出，梯度下降不一定能够找到全局最优解，有可能是局部最优解，但此种方法已能帮助我们求解Logistic回归问题。另外如果求解的函数是凸函数，梯度下降法得到得解一定是全局最优解。

4.2 梯度下降算法相关概念

求解梯度下降算法之前，我们先了解相关概念。

• 步长（Learning Rate）：步长决定梯度下降算法过程中，每步沿梯度负方向前进的长度。
• 特征（Feature）：即上述描述的$X$
• 假设函数（Hypothesis Function）：监督学习中，为了拟合输入样本，而使用假设函数。
• 损失函数（Loss Function）：为了评估模型拟合的好坏，通常用损失函数来度量拟合的程度。损失函数极小，意味着拟合的程度越好，对应的模型参数即为最优参数。Logistic损失函数为

$$J(\theta )=-\frac{1}{m}\left\{\sum _{i=1}^m-ln[1+e^{{\theta }^{T}x}]+\sum _{i=1}^m{y}_i{\theta }^{T}X\right\}$$

我们利用梯度下降算法，目标便是找到一组$\theta$使得$J(\theta )$达到最小。

4.3梯度下降算法过程

• 随机选取一组$\theta$。
• 不断变化$\theta$，让$J(\theta )$变小，$\alpha$为学习步长。

$${\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J(\theta )$$

• 直到$J(\theta )$得到最小值，$\frac{\partial }{\partial {\theta }_k}J(\theta )$为$J(\theta )$对${\theta }_k$的偏导。

$$\frac{\partial J(\theta )}{\partial {\theta }_j}=\frac{1}{m}\sum _{i=1}^m\frac{1}{1+e^{{\theta }^{T}X}}{e}^{{\theta }^{T}X}{X}_{ij}-\sum _{i=1}^m{y}_i{X}_{ij}$$

$$=\frac{1}{m}\sum _{i=1}^m{X}_{ij}[\frac{e^{{\theta }^{T}X}}{1+e^{{\theta }^{T}x}}-y_i]$$

$$=\frac{1}{m}\sum _{i=1}^m{X}_{ij}[\pi (X_i)-y_i]$$

因此梯度下降算法的迭代最终表述为
$${\theta }_j:={\theta }_j-\alpha \frac{1}{m}\sum _{i=1}^m{X}_{ij}[\pi (X_i)-y_i]$$
梯度下降算法需多次迭代、算法复杂度为$O(k{n}^2)$。当利用梯度下降算法求得一组$\theta$时我们便能得到Logistic函数。

5.Logistic回归实现

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler

def plot_decision_regions(X, y, classifier, test_idx=None, resolution=0.02):
    # setup marker generator and color map
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'cyan', 'gray')
    cmap = ListedColormap(colors[:len(np.unique(y))])
    # plot the decision surface
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), np.arange(x2_min, x2_max, resolution))
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
    Z = Z.reshape(xx1.shape)
    plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
    plt.xlim(xx1.min(), xx1.max())
    plt.ylim(xx2.min(), xx2.max())
    # plot class samples
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],alpha=0.8, c=cmap(idx),marker=markers[idx], label=cl)
    # highlight test samples
    if test_idx:
        X_test, y_test = X[test_idx, :], y[test_idx]
        plt.scatter(X_test[:, 0], X_test[:, 1], c='blue', alpha=1.0, linewidth=1, marker='o', s=55, label='test set')

iris = datasets.load_iris()
X = iris.data[:, [2, 3]]
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
#为了追求机器学习的最佳性能，我们将特征缩放
sc = StandardScaler()
sc.fit(X_train)#估算每个特征的平均值和标准差
X_train_std=sc.transform(X_train)#用同样的参数来标准化测试集，使得测试集和训练集之间有可比性
X_test_std=sc.transform(X_test)
X_combined_std = np.vstack((X_train_std, X_test_std))
y_combined = np.hstack((y_train, y_test))

#训练感知机模型
lr = LogisticRegression(C=1000.0,random_state=0)#迭代次数为1000次,random_state设置随机种子，每次迭代都有相同的训练集顺序
lr.fit(X_train_std, y_train)
lr.predict_proba(X_test_std)

#绘图
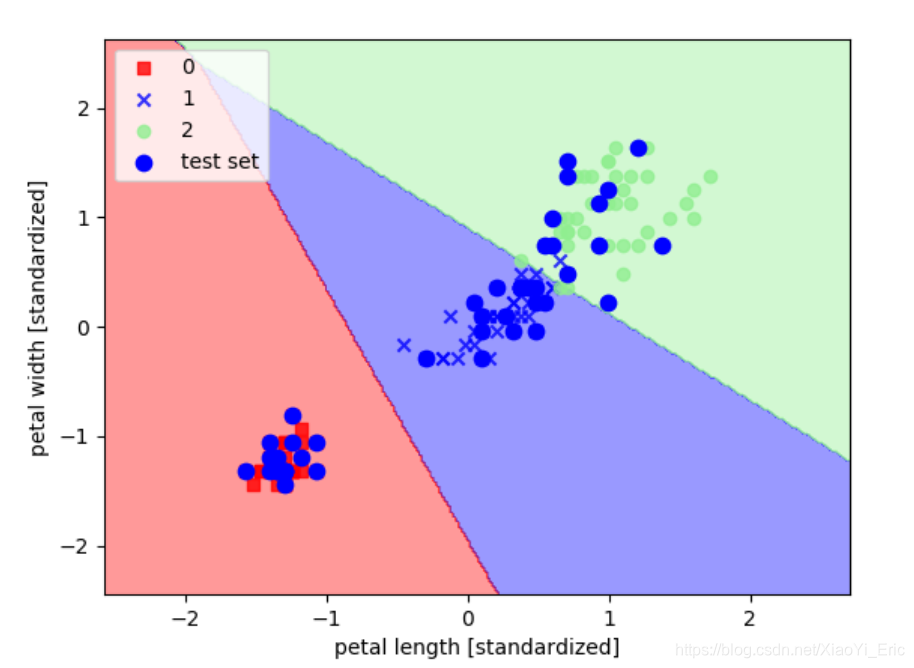
plot_decision_regions(X_combined_std, y_combined, classifier=lr, test_idx=range(105,150))
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.show()

• 参考
  [1]:https://www.zhihu.com/people/maigo/activities
  [2]:https://blog.youkuaiyun.com/programmer_wei/article/details/52072939
  [3]:https://blog.youkuaiyun.com/javaisnotgood/article/details/78873819