机器视觉学习-day18-霍夫变换

霍夫变换可以检测图像中直线、圆等其他形状。基本思想是将图像空间（原始空间）的点映射到参数空间（霍夫空间）中，通过参数空间中寻找最大值来实现检测。

代码运行步骤：图片输入→灰度化→Canny算法→霍夫变换→图片输出

1 霍夫直线变换

对于一条直线（不垂直于x轴），可以 y=kx+b 来表示，此时x和y是横纵坐标，k和b是固定参数，对上面的公式进行变换：b=-kx+y

此时，以k和b为横纵坐标，x和y为固定参数，前后如下所示。

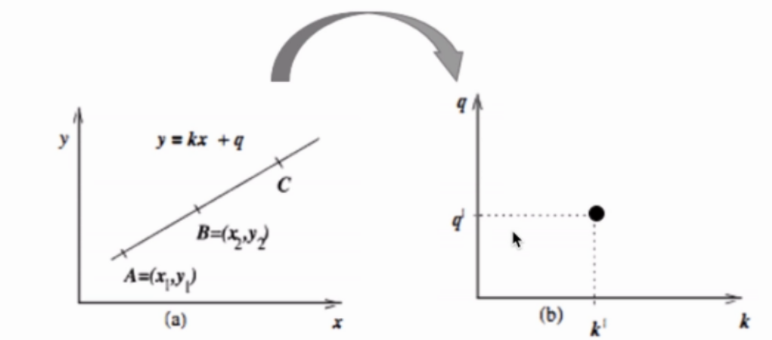
从上图中可以看出，在直角坐标系下的一条直线，在变换后的空间中仅仅表示为一点，对于变换后的空间，称之为霍夫空间。

原始空间的直角坐标系下一条无限长的直线对应了霍夫空间中的一个点，霍夫空间的一条直线对应了原始空间的直角坐标中的一个点。

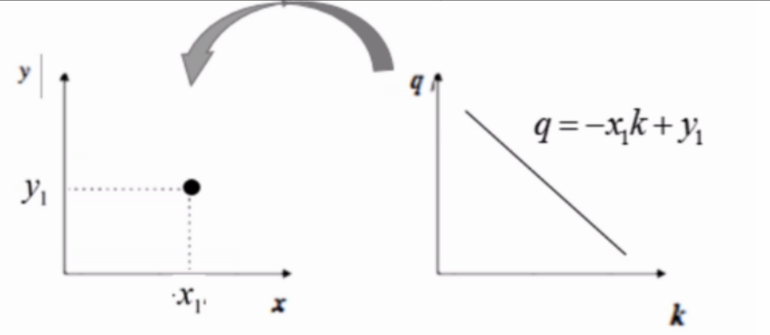
一个二值化的图像，前景可能是一些白色像素散点，每个点在霍夫空间中都是一条直线，当霍夫空间的两条直线相交时，表示原始空间中两个点之间的连线。相反的，在原始空间中有n条直线相交与一点，在霍夫空间中就是n个点共线。

利用上述现象，可以通过霍夫空间的现象，找到原始空间的特征。

• 如果霍夫空间中有很多线相交于一点，表示可以找到原始空间中很多点构成的一条线。

• 如果霍夫空间中有很多点共线，表示可以找到原始空间中很多线相交的点。

对于垂直与x轴的直线，由于斜率无穷大，导致无法使用上述的空间变换。解决的方法是在原始空间中，不再使用斜率和截距表示直线，而更换为极坐标系。

• 极径 ρ

该点到原点的距离

• 极角 θ

从正x轴到该点与极径的夹角，逆时针为正

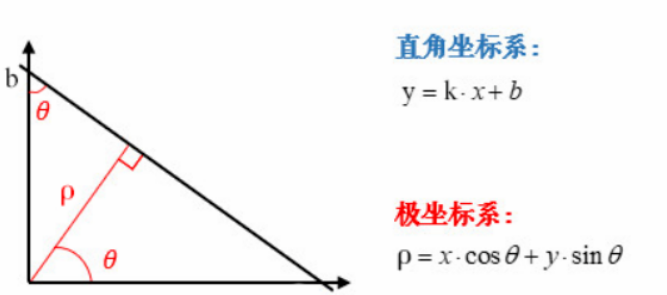
使用极坐标系的目的是让霍夫空间可以表示原始空间，对于原始空间还是使用直角坐标系。

原始空间（笛卡尔坐标系）→ 原始空间（极坐标系）→ 霍夫空间（极坐标系）

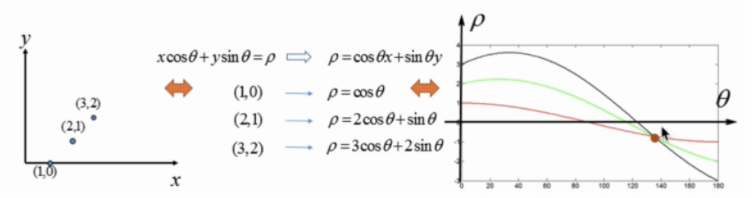
投票规则：根据上图，霍夫空间在极坐标系下，原始空间的一个点可以在霍夫空间中产生一条三角函数曲线，多条三角函数的曲线可能相交于一点，因此可以设定一个阈值，来检测霍夫空间中三角函数曲线相交的次数，如果一个交点的三角函数相交次数超过阈值，这个交点代表的原始空间直线可能是寻找的目标直线。

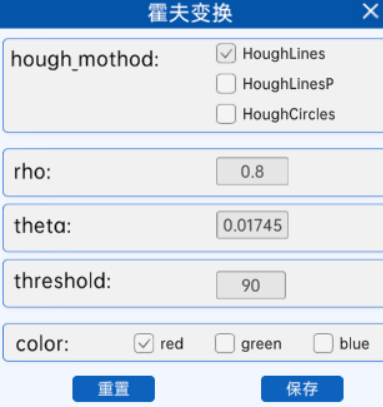
观察虚拟仿真实验中霍夫变换节点的参数：

• hough_method：选择HoughLines表示霍夫直线变换

• rho：极径 ρ的密度，值越大表示在单位面积内累加器格子的数量越大，常见的范围是1到图像宽度或高度的一半

• theta：极角 θ的密度，值越大表示在单位面积内累加器格子的数量越大，常见的范围是0到π，建议选择π/180，即1度

• threshold：累加器阈值，值越大表示在原始空间中识别越少的线，常见的范围是50-200，具体的值取决于图像的复杂度和噪声水平