堆、栈、队列的区别以及使用场景

转载自：https://www.pianshen.com/article/54131761085/

 

1. 堆和栈

JavaScript中的变量分为基本类型和引用类型：

• 基本类型是保存在栈内存中的简单数据段，它们的值都有固定的大小，每种类型的数据占用的内存空间的大小是确定的，并由系统自动分配和自动释放，通过按值访问。

• 引用类型是保存在堆内存中的对象，值大小不固定，栈内存中存放的该对象的访问地址指向堆内存中的对象，JavaScript不允许直接访问堆内存中的位置，因此操作对象时，实际操作对象的引用。
  

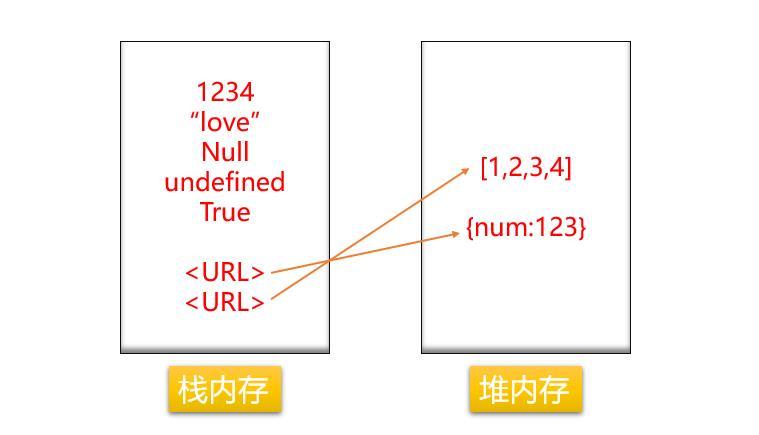
所以对于堆和栈;

• 栈：栈是一种线性的数据结构，读取规则是先进后出。栈中的数据占用的内存空间的大小是确定的，便于代码执行时的入栈、出栈操作，并由系统自动分配和自动释放内存可以及时得到回收，相对于堆来说，更加容易管理内存空间。

• 堆：堆是一种树形数据结构，读取相对复杂。堆是动态分配内存，内存大小不一，也不会自动释放。栈中的数据长度不定，且占空间比较大。便于开辟内存空间，更加方便存储。

堆栈内存分配：

程序运行时，每个线程分配一个栈，每个进程分配一个堆。也就是说，栈是线程独占的，堆是线程共用的。此外，栈创建的时候，大小是确定的，数据超过这个大小，就发生stack overflow错误，而堆的大小是不确定的，需要的话可以不断增加。

2. 栈和队列

（1）队列

队列是一种先进先出的数据结构。 队列在列表的末端增加项，在首端移除项。它允许在表的首端（队列头）进行删除操作，在表的末端（队列尾）进行插入操作；

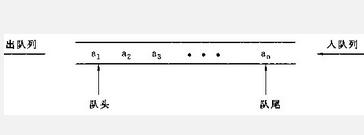
（2）栈

• 栈是一种后进先出的数据结构，也就是说最新添加的项最早被移出；它是一种运算受限的线性表，只能在栈顶进行插入和删除操作。向一个栈插入新元素叫入栈（进栈），就是把新元素放入到栈顶的上面，成为新的栈顶；从一个栈删除元素叫出栈，就是把栈顶的元素删除掉，相邻的成为新栈顶。
  

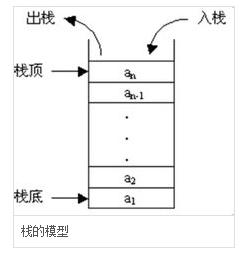
应用场景：

• 栈可以用于字符匹配，数据反转等场景
• 队列可以用于任务队列，共享打印机等场景
• 堆可以用于优先队列，堆排序等场景