使用LaTeX表达MATLAB绘图中的常见公式
为什么使用LaTeX?
Latex具有强大的显示数学公式的能力,能轻松表达出复杂的数学公式且非常美观。
例1:
f=@(x)exp(-2*x);
x=0:0.1:2;
plot(x,f(x),'.-k');
xlabel('{\itx}'); %{\it }表示以斜体输入,下同
ylabel('{\ity=e^{-2x}}');
legend('f(x)=e^{-2x}');
f=@(x)exp(-2*x);
x=0:0.1:2;
plot(x,f(x),'.-k');
xlabel('{\itx}'); %{\it }表示以斜体输入,下同
ylabel('{\ity=e^{-2x}}');
latexf=['$$f(x)=e^{-2x}$$'];
lgh=legend(latexf);
set(lgh,'interpreter','latex');
第一个程序写出的数学公式
第二个程序使用LaTeX写法写出的数学公式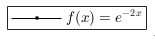
常见数学符号的表达方法:
1.上下标
用^来表示上标,用 _ 来表示下标,如果多于一个字符则用{}括起来。其他数学符号也经常使用上下标来表示,比如求和、积分、极限等。
例2:
x1=0:0.1:10;
y=3*x1.^2+4*x1+5;
plot(x1,y);
xlabel('{\itx}');
ylabel('{\ity=3x{^2_1}}'); %注意此处x既有上标又有下标的写法
latexf=['$$y(x)=3x{^2_1}+4x_1+5$$'];
lgh=legend(latexf);
set(lgh,'interpreter','latex');
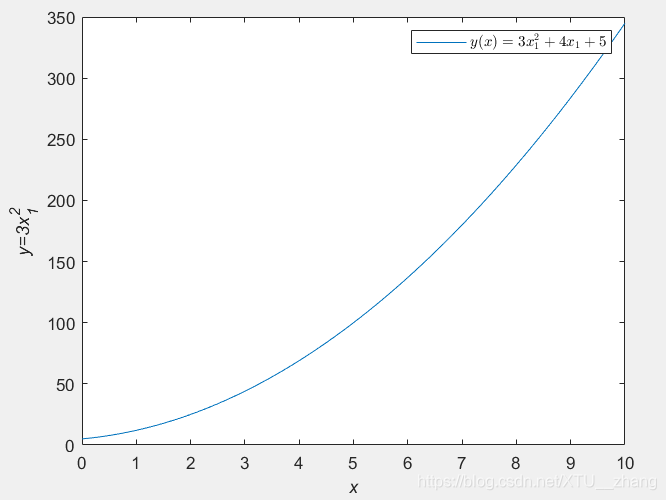
2.分数
使用下式表示分数,其中numerator表示分子,denominator表示分母。
\frac{numerator}{denominator}
例3:
x=0:0.1:10;
y=x.^3+(7*x)/(2*x.^2+1);
plot(x,y);
xlabel('{\itx}');
latexy=['$$y=x^3+\frac{7x}{2x^2+1}$$']; %表示分数
ylbh=ylabel(latexy);
set(ylbh,'interpreter','latex');
latexf=['$$y(x)=x^3+\frac{7x}{2x^2+1}$$'];
lgh=legend(latexf);
set(lgh,'interpreter','latex');
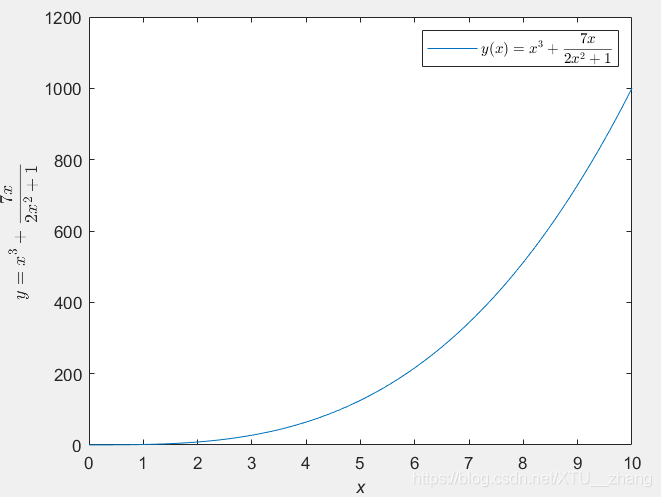
3.开方
使用下式表示开平方:
\sqrt{expression}
使用下式表示开n次方:
\sqrt[n]{expression}
例4:
x=1:0.1:10;
y=(x./2.*x+1).^(1/3);
plot(x,y);
xlabel('{\itx}');
latexy=['$$y=\sqrt[3]{\frac{x}{2x+1}}$$']; %开三次方
ylbh=ylabel(latexy);
set(ylbh,'interpreter','latex');
latexf=['$$y=\sqrt[3]{\frac{x}{2x+1}}$$'];
lgh=legend(latexf);
set(lgh,'interpreter','latex');
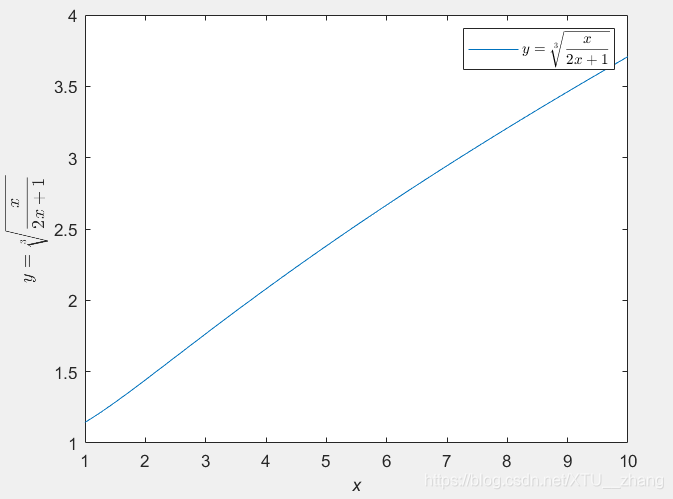
4.求和
使用下式表示求和:
\sum_{initial}^end expression
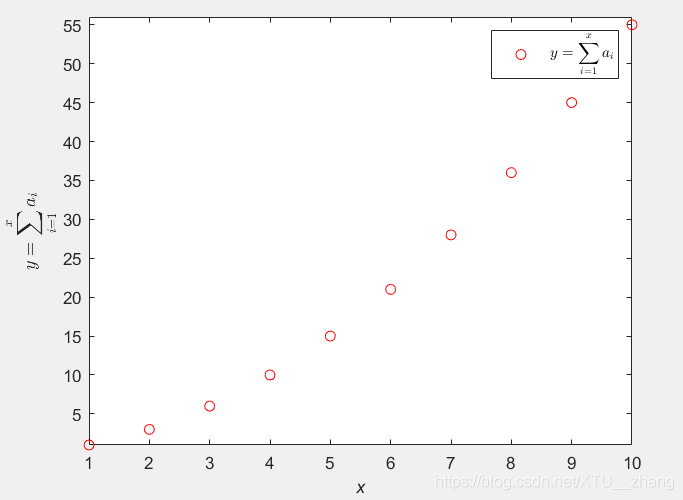
例5:
x=1:1:10;
y=cumsum(x); %逐项求和
plot(x,y,'ro');
ylim([1,56]);
xlabel('{\itx}');
latexy=['$$y=\sum_{i=1}^x a_i$$']; %用latex表示求和
ylbh=ylabel(latexy);
set(ylbh,'interpreter','latex');
latexf=['$$y=\sum_{i=1}^x a_i$$'];
lgh=legend(latexf);
set(lgh,'interpreter','latex');
5.大括号
使用下式分别表示左右大括号:
\left( 和 \right)
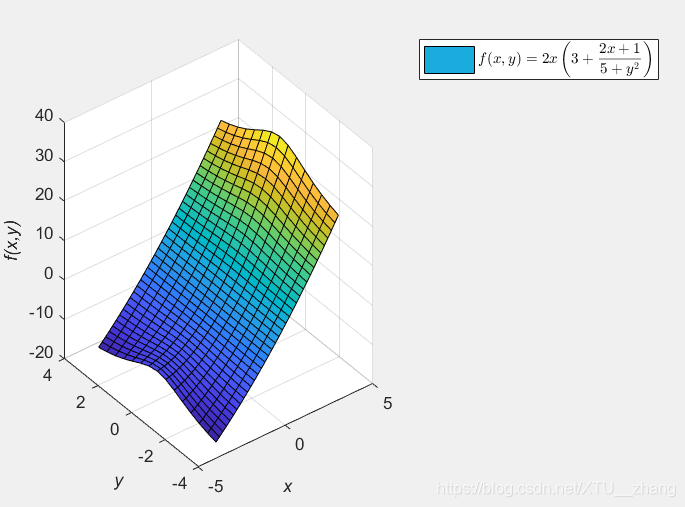
例6:
x=-3.5:0.2:3.5;
y=-3.5:0.5:3.5;
[X,Y]=meshgrid(x,y);
Z=2*X.*(3+(X.*2+1)./(5+Y.^2));
surf(X,Y,Z);
xlabel('{\itx}');
ylabel('{\ity}');
zlabel('\itf(x,y)');
latexf=['$$f(x,y)=2x\left(3+\frac{2x+1}{5+y^2}\right)$$']; %大括号
lgh=legend(latexf);
set(lgh,'interpreter','latex');
6.积分
使用下式表示积分:
\int_{initial}^{end} expression
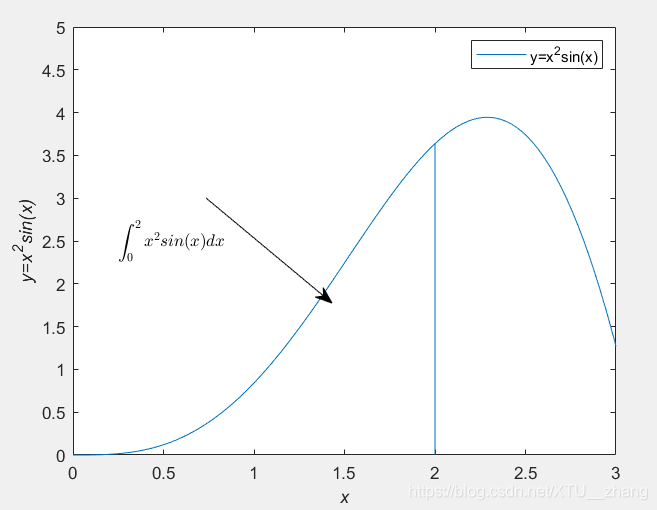
例7:
x=linspace(0,3);
y=x.^2.*sin(x);
plot(x,y);
ylim([0,5]);
line([2,2],[0,2^2*sin(2)]); %画一条竖线,表示积分终点
str='$$\int_{0}^{2} x^2sin(x) dx$$'; %用latex表示积分
text(0.25,2.5,str,'Interpreter','latex'); %写文本
annotation('arrow','X',[0.32,0.5],'Y',[0.6,0.4]); %为文本画一个箭头
xlabel('{\itx}');
ylabel('{\ity=x^2sin(x)}');
legend('y=x^2sin(x)');
7.极限
用下式表示极限:
\lim_{variable \to numbel} expression
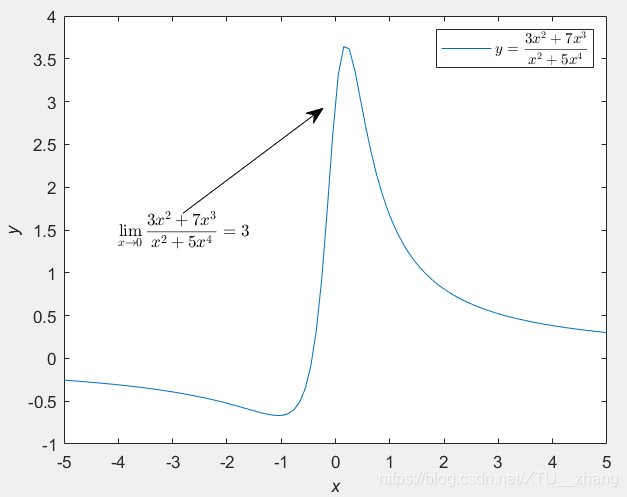
例8:
x=linspace(-5,5);
y=(3.*x.^2+7.*x.^3)./(x.^2+5.*x.^4);
plot(x,y);
ylim([-1,4]);
str='$$\lim_{x \to 0} \frac{3x^2 +7x^3}{x^2 +5x^4} = 3$$'; %表示极限
text(-4,1.5,str,'Interpreter','latex');
annotation('arrow','X',[0.3,0.5],'Y',[0.55,0.75]);
xlabel('{\itx}');
ylabel('{\ity}');
latexf=['$$y=\frac{3x^2+7x^3}{x^2+5x^4}$$'];
lgh=legend(latexf);
set(lgh,'interpreter','latex');
8.导数符号和偏导数符号
导数符号直接用分数以及dy、dx之类表示即可
偏导符号则可用
\partial
表示。
例9:
x=1:0.1:2; %此程序仅为展示偏导数的写法,所以随便取的数值。
y=1;
plot(x,y);
latexf=['$$\frac{\partial u}{\partial t}= h^2 \left( \frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}+\frac{\partial^2 u}{\partial z^2}\right)$$'];
lgh=legend(latexf);
set(lgh,'interpreter','latex');
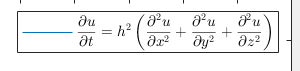
9.省略号
可以用下式表示和底端对齐的省略号:
\ldots
用下式表示和中线对齐的省略号:
\cdots
例10:
x=1:0.1:2; %此程序仅为展示省略号的写法,所以随便取的数值。
y=1;
plot(x,y);
latexf=['$$f(x_1,x_2,\ldots,x_n) = x_1^2 + x_2^2 + \cdots + x_n^2$$'];
lgh=legend(latexf);
set(lgh,'interpreter','latex');
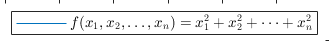





 本文详细介绍了如何使用LaTeX在MATLAB绘图中优雅地表达常见数学公式,包括上下标、分数、开方、求和、大括号、积分、极限、导数符号和偏导数符号,以及省略号的表示方法。通过实例展示LaTeX的强大之处,提升图表的专业性与美观性。
本文详细介绍了如何使用LaTeX在MATLAB绘图中优雅地表达常见数学公式,包括上下标、分数、开方、求和、大括号、积分、极限、导数符号和偏导数符号,以及省略号的表示方法。通过实例展示LaTeX的强大之处,提升图表的专业性与美观性。
















 1967
1967

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








