数据结构——二叉树（层序遍历）

一.层序遍历一棵二叉树

思路如图：

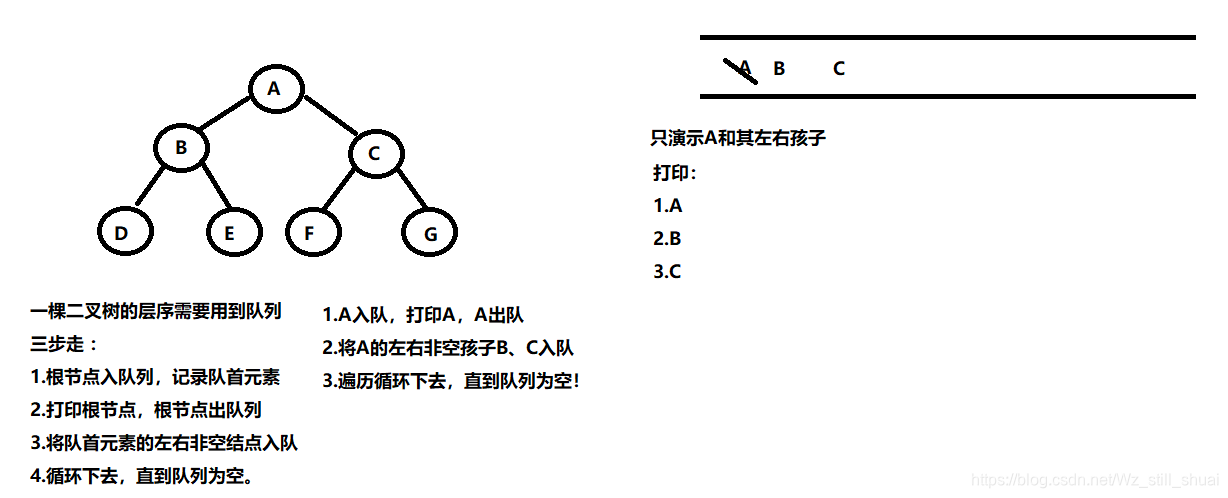
代码：

//对二叉树进行层序遍历
void levOrder(Tree* root) {
	
	if (root == NULL) {
		return;
	}
	//根结点入队
	//打印根节点，根节点出队
	//根节点的左右非空孩子入队
	std::queue <Tree*> queue;
	queue.push(root);
	while (!queue.empty()) {
		Tree* front = queue.front();
		queue.pop();
		printf("%c  ", front->val);
		if (front->left) {
			queue.push(front->left);
		}
		if (front->right) {
			queue.push(front->right);
		}
	}
}

二.判断一棵二叉树是否是完全二叉树

完全二叉树：倒数第二层结点数达到该层结点的最大数，最后一层叶子节点均在上层节点的左子树。

也是层序遍历的应用：

 

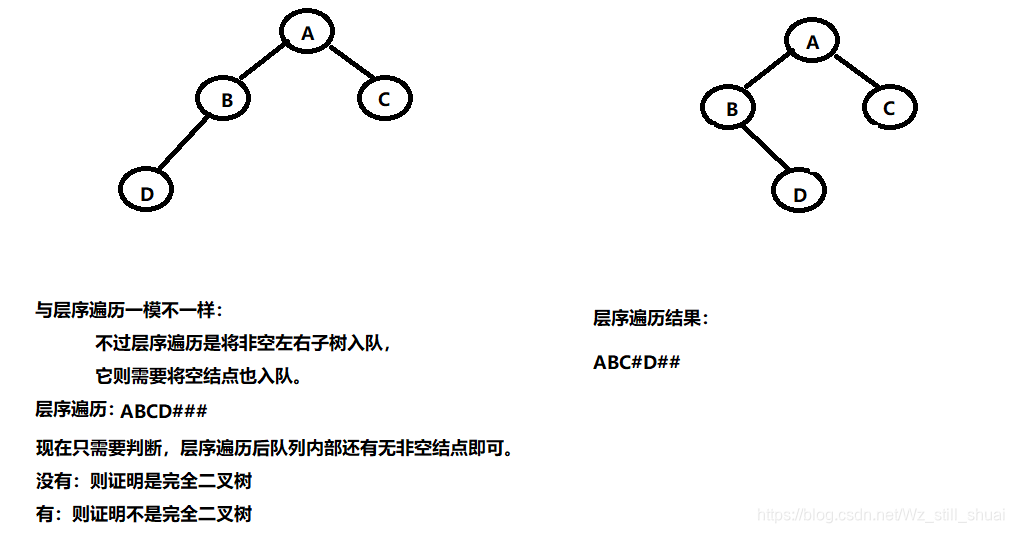
所以与层序不同的只是需要将空结点也入队。

代码：

//判断二叉树是否是完全二叉树
bool isComplete(Tree* root) {
	//将空结点也入队，最后判断队内有没有非空元素即可，
	std::queue <Tree*> q;
	q.push(root);
	while (true) {
		Tree* front = q.front();
		q.pop();
		//如果队首第一次为空，就退出循环
		if (front == NULL) {
			break;
		}
		//将空结点也入队
		q.push(front->left);
		q.push(front->right);
	}
	//将队内进的空结点出队，判断是否还有没有非空结点
	//若有，则表明不是完全二叉树
	//没有，则表明是完全二叉树
	while (!q.empty()) {
		Tree* front = q.front();
		q.pop();
		if (front != NULL) {
			return false;
		}
	}
	return true;
}