目前博主也只学到了这里,关于数据结构之后会稍微断更,见谅。
回顾:数据的逻辑结构
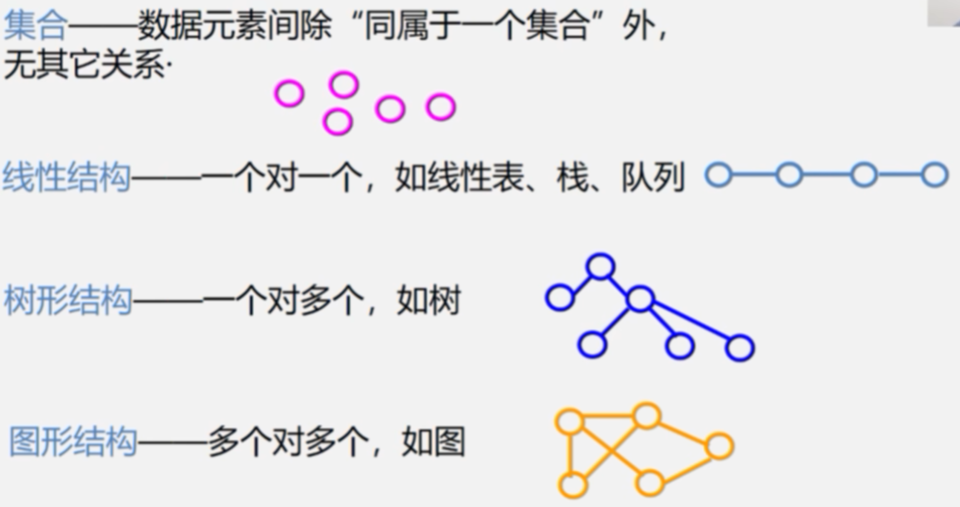
6.1图的定义和基本术语
定义
图
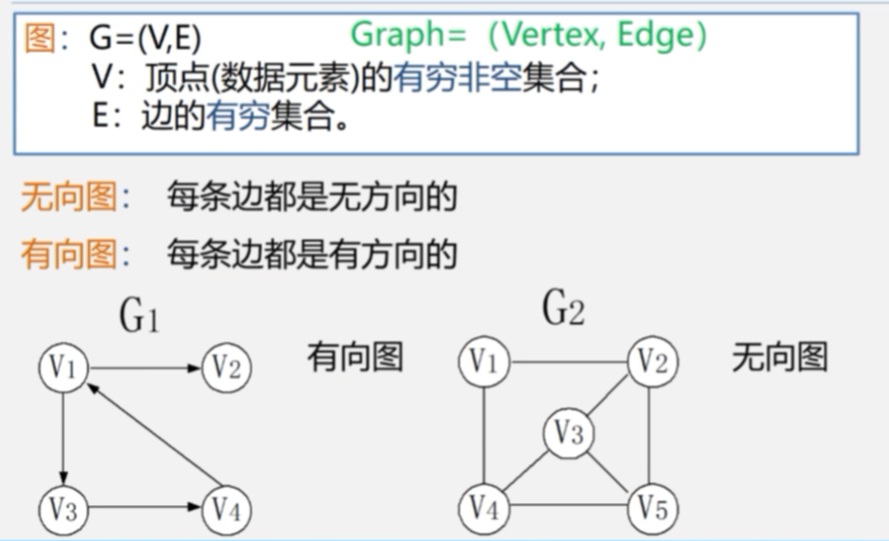
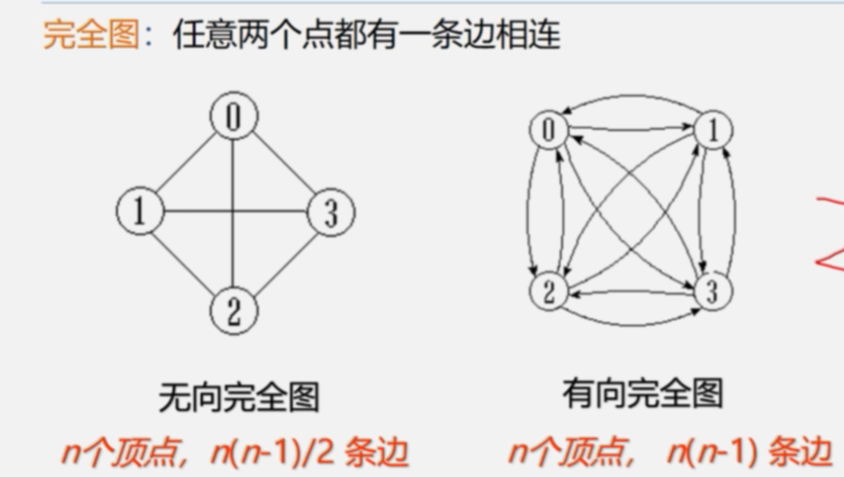

顶点的度
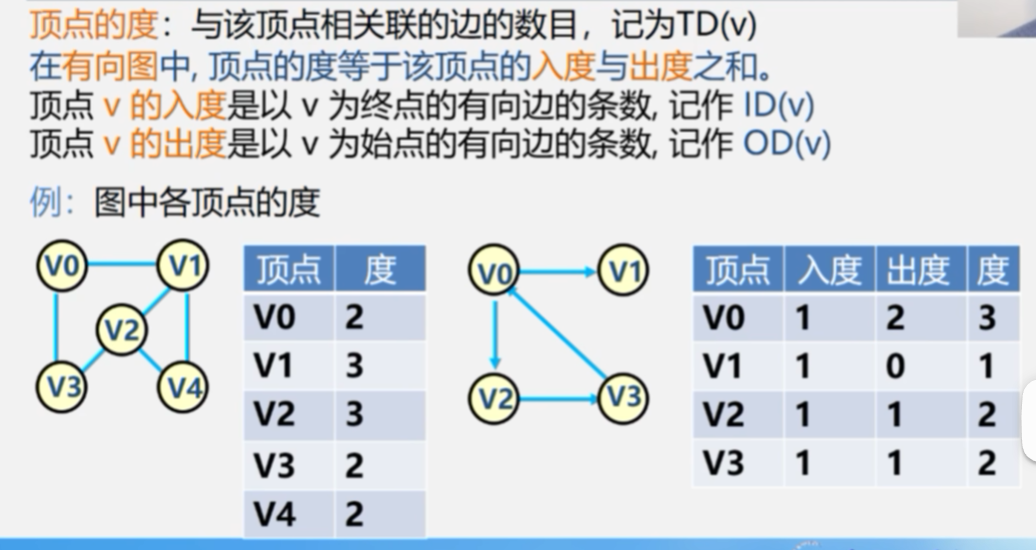
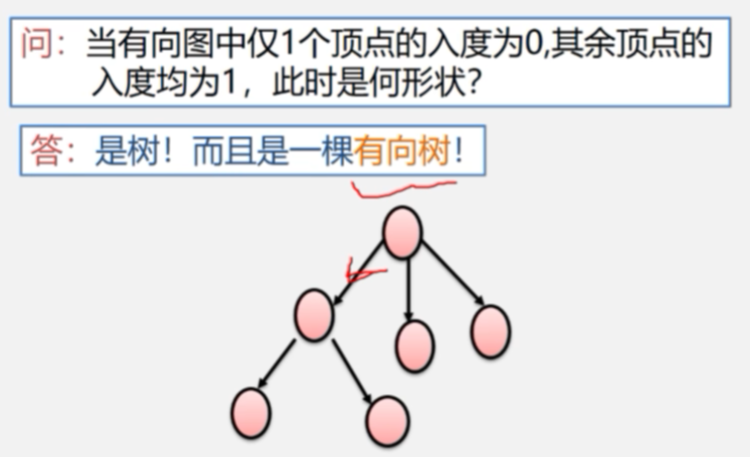
路径
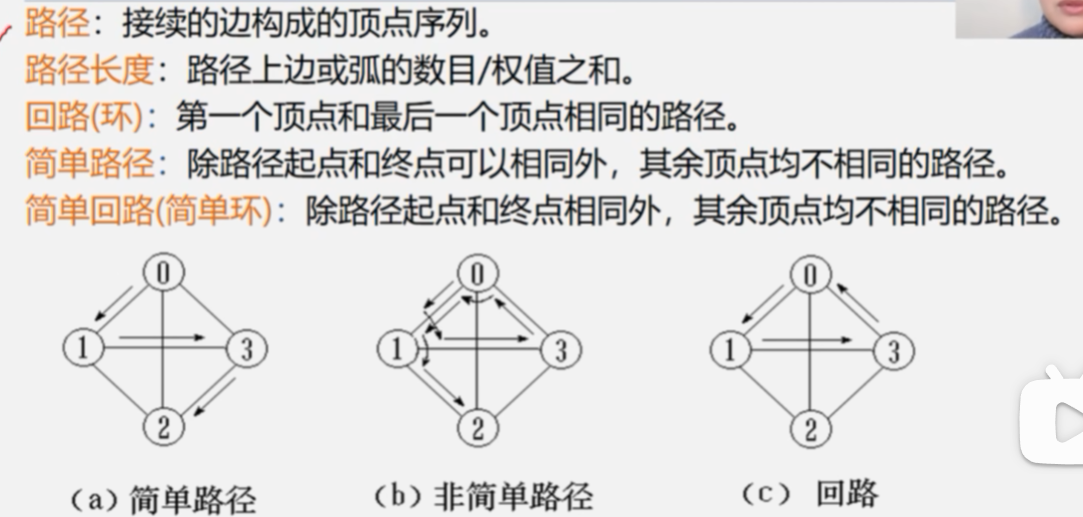
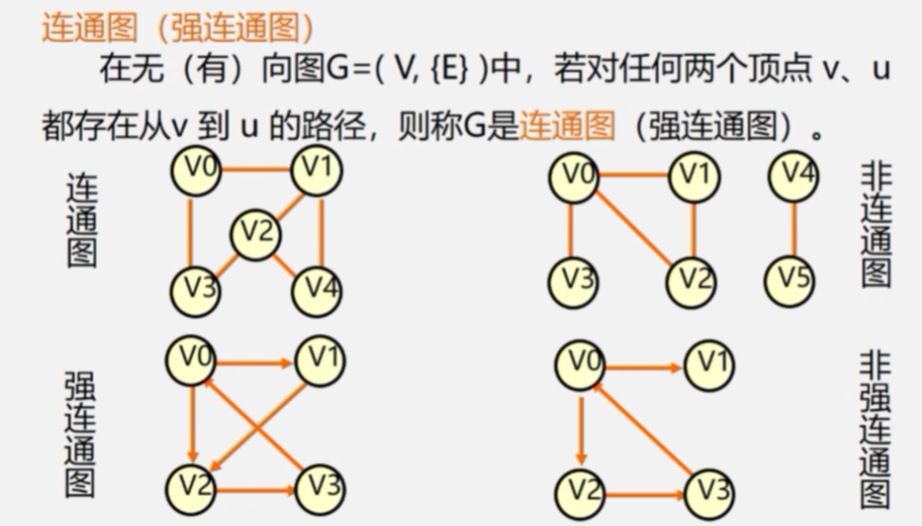
连通图
权与网
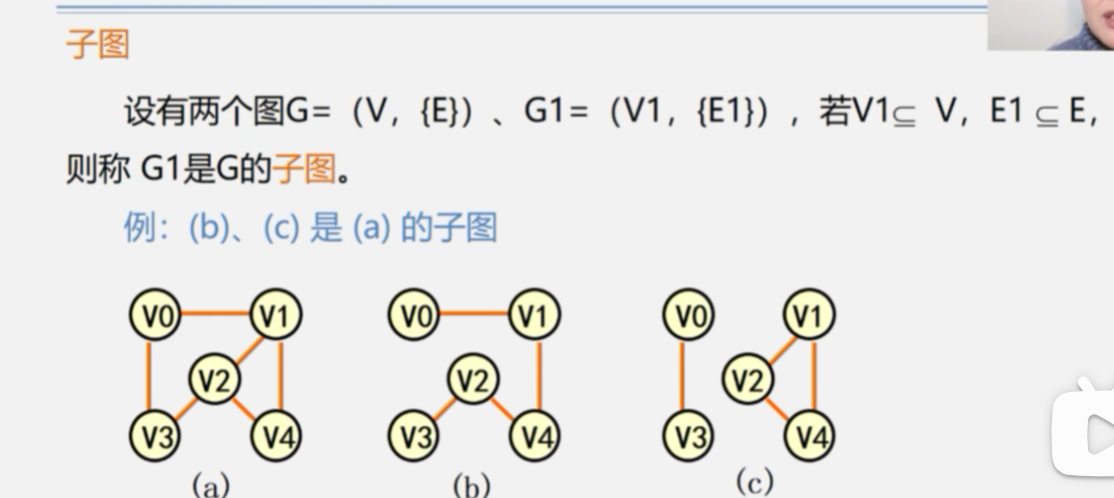
子图
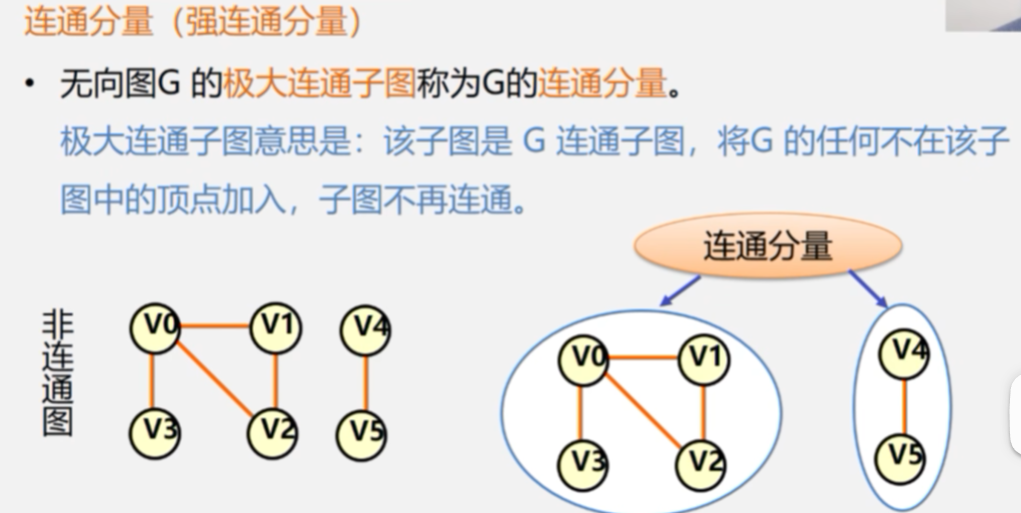
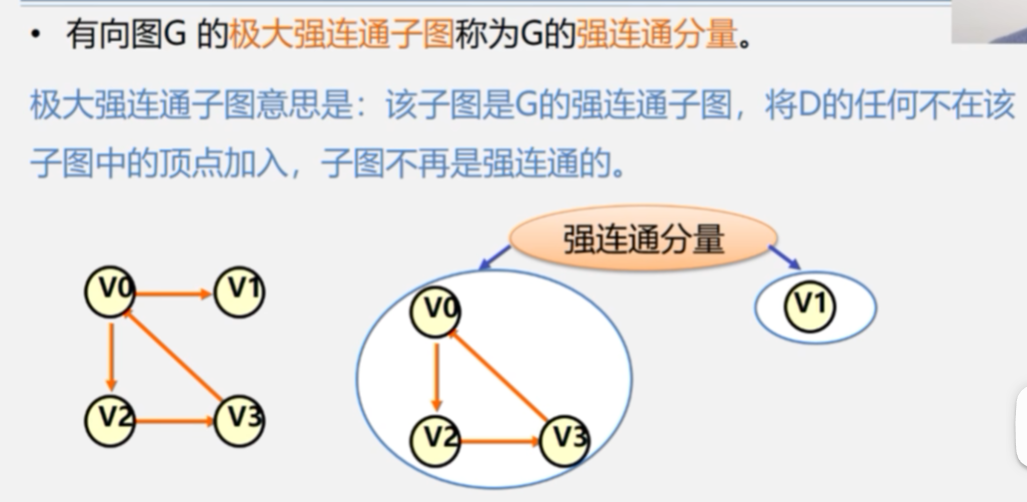
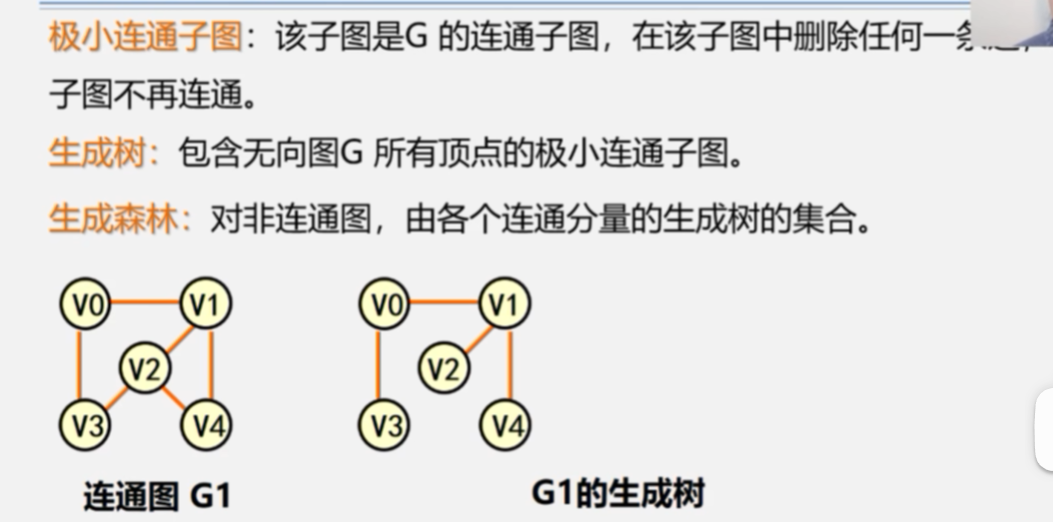
连通分量
6.2案例引入
案例6.1:六度空间理论


6.3图的类型定义



6.4图的存储结构
6.4.1邻接矩阵
1.数组(邻接矩阵)表示法
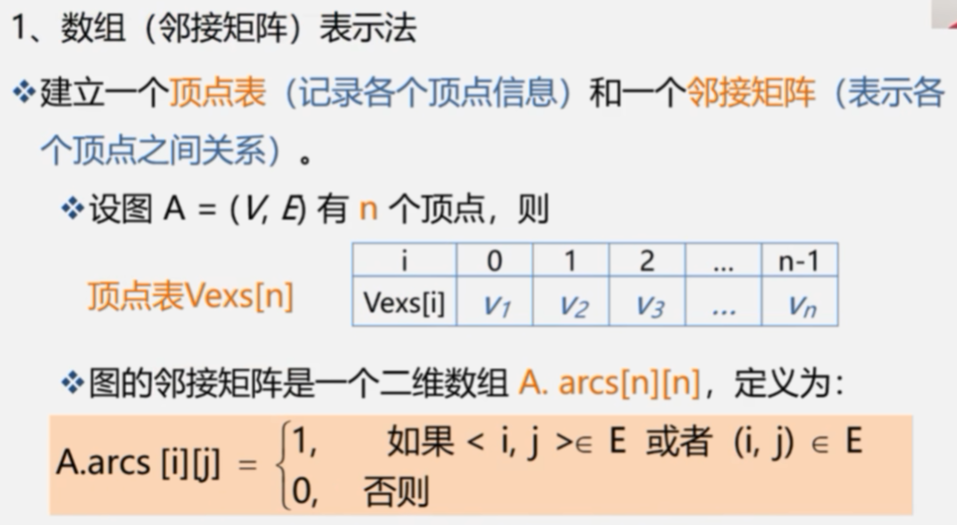

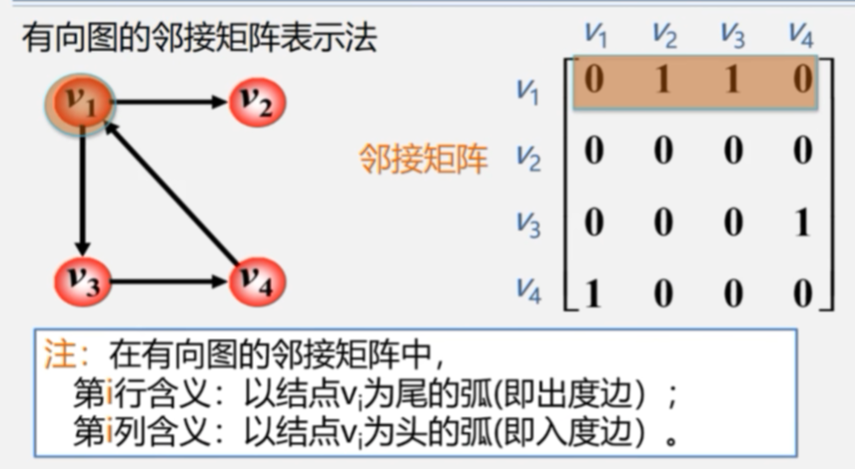
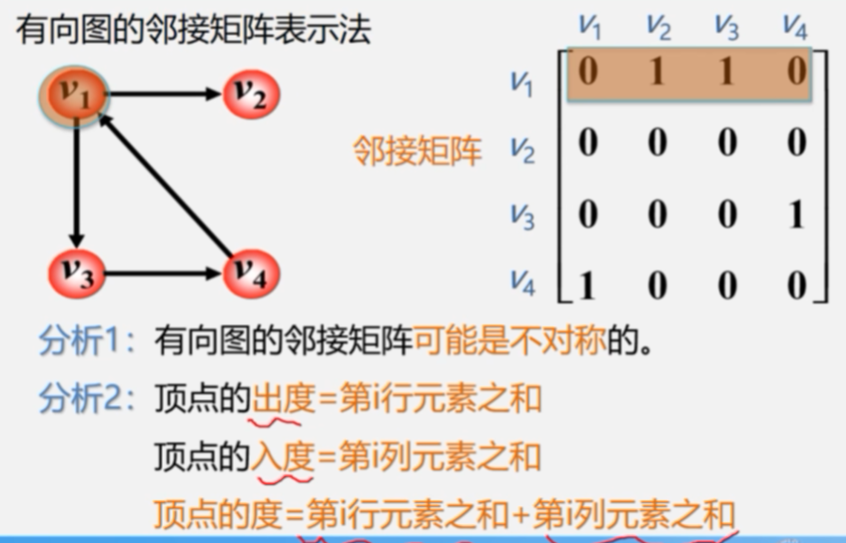
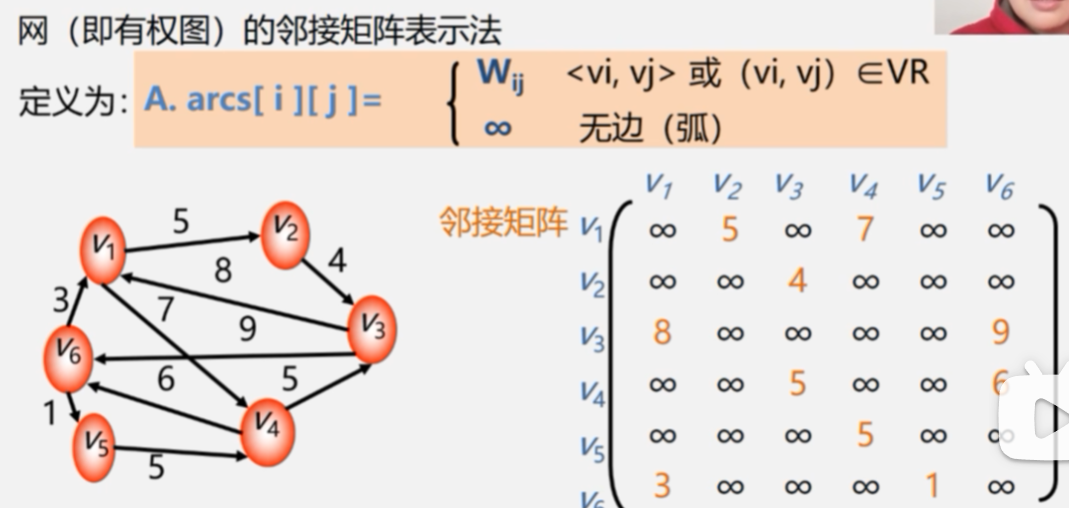

#define MaxInt 32767 // 表示极大值,即∞
#define MVNum 100 // 最大顶点数
typedef char VerTexType; // 设顶点的数据类型为字符型
typedef int ArcType; // 假设边的权值类型为整型
// 邻接矩阵图结构
typedef struct {
VerTexType vexs[MVNum]; // 顶点表
ArcType arcs[MVNum][MVNum]; // 邻接矩阵
int vexnum, arcnum; // 图的当前点数和边数
} AMGraph; // Adjacency Matrix Graph

2.采用邻接矩阵表示法创建无向网


算法 6.1 采用邻接矩阵表示法创建无向网
Status CreateUDN(AMGraph &G) {
// 采用邻接矩阵表示法,创建无向网G
cin >> G.vexnum >> G.arcnum; // 输入总顶点数,总边数
for (int i = 0; i < G.vexnum; ++i)
cin >> G.vexs[i]; // 依次输入顶点的信息
// 初始化邻接矩阵
for (int i = 0; i < G.vexnum; ++i)
for (int j = 0; j < G.vexnum; ++j)
G.arcs[i][j] = MaxInt; // 边的权值均置为极大值
for(k = 0; k < G.arcnum; ++k){ //构造邻接矩阵
cin>>v1>>>v2>>>w; //输入一条边所依附的顶点及边的权值
i = LocateVex(G, v1);
j = LocateVex(G, v2); //确定v1和v2在G中的位置
G.arcs[i][j] = w; //边<v1, v2>的权值置为w
G.arcs[j][i] = G.arcs[i][j]; //置<v1, v2>的对称边<v2, v1>的权值为w
}//for
return OK;
}//CreateUDN
补充算法:在图中查找顶点
int LocateVex(AMGraph G, VertexType u) {
//图G中查找顶点u,存在则返回顶点表中的下标;否则返回-1
int i;
for(i=0;i<G.vexnum;+ +i)
if(u==G.vexs[i]) return i;
return -1;
}


6.4.2邻接表
1.邻接表表示法
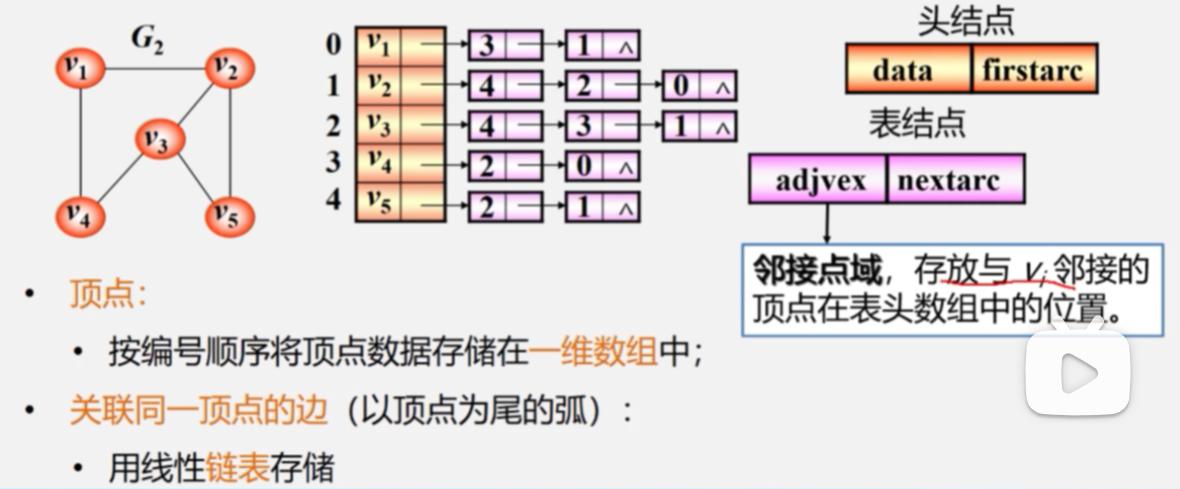
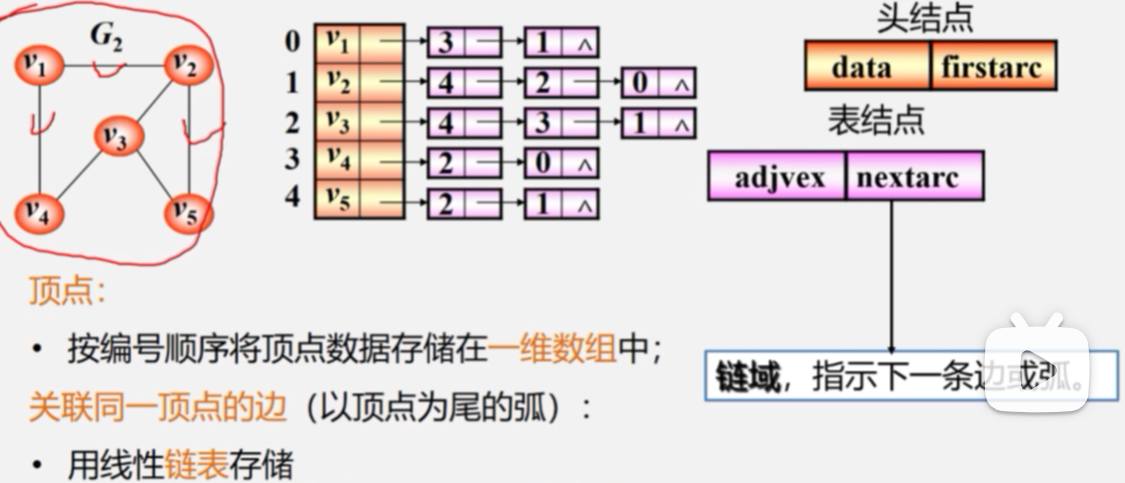
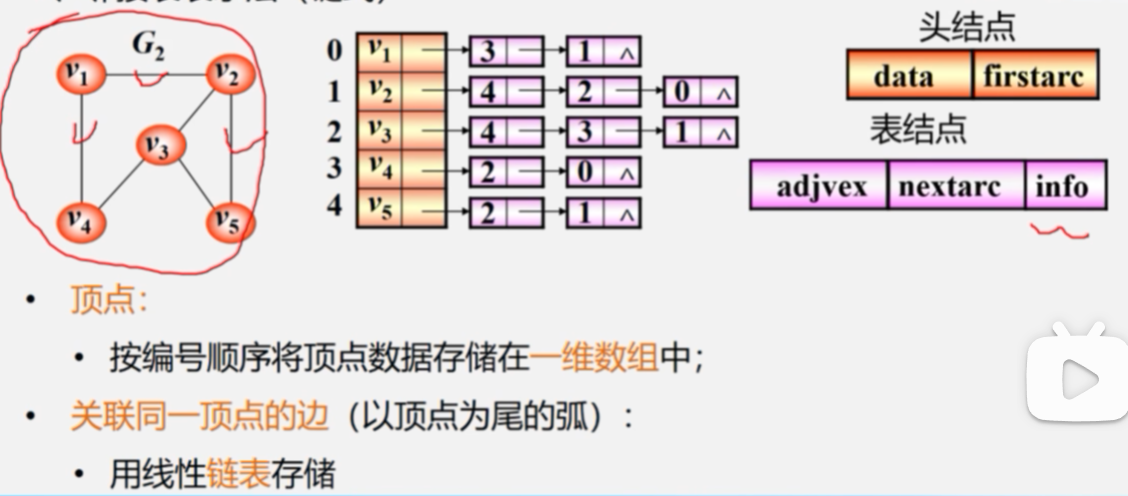
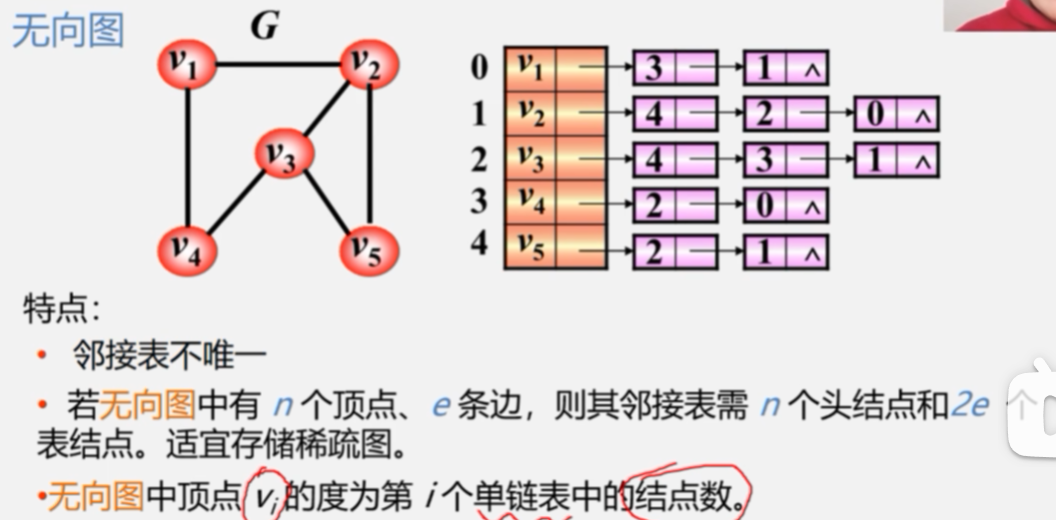
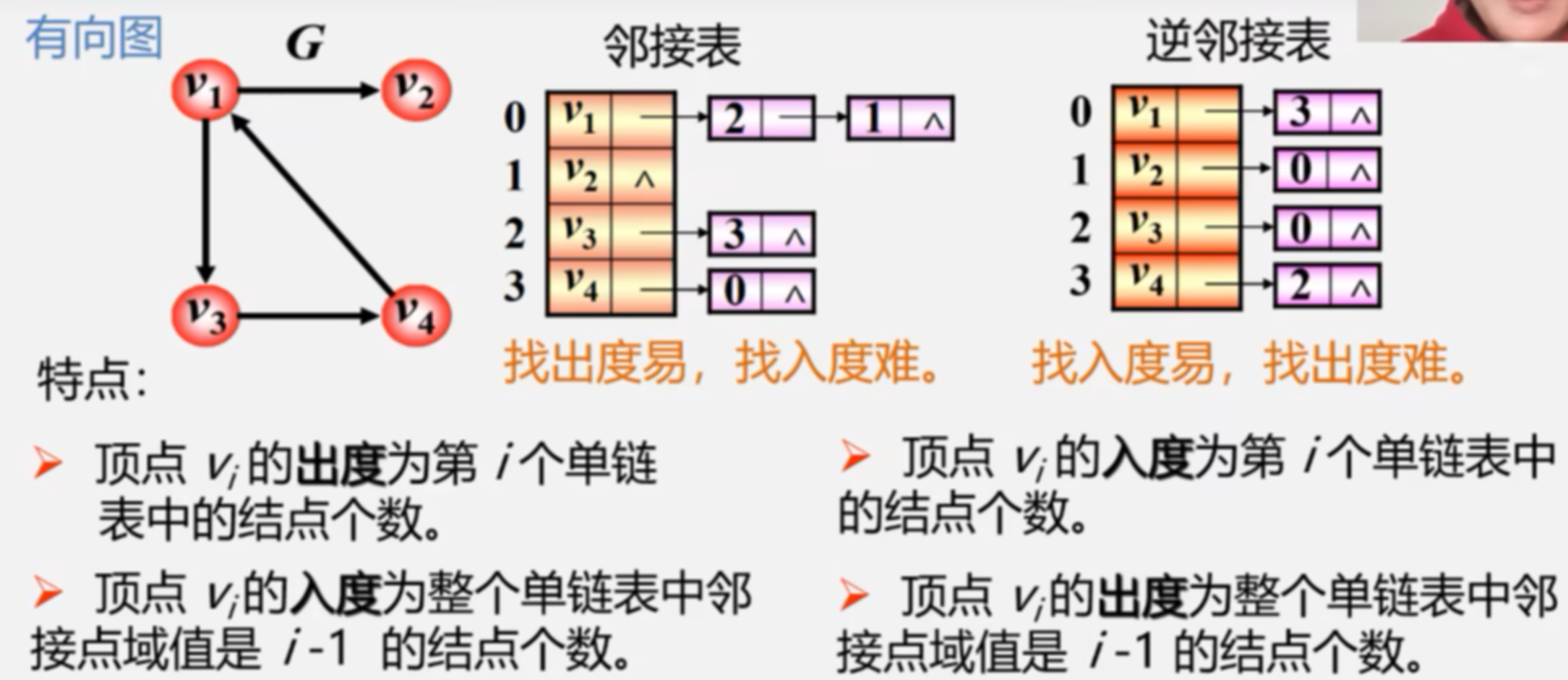
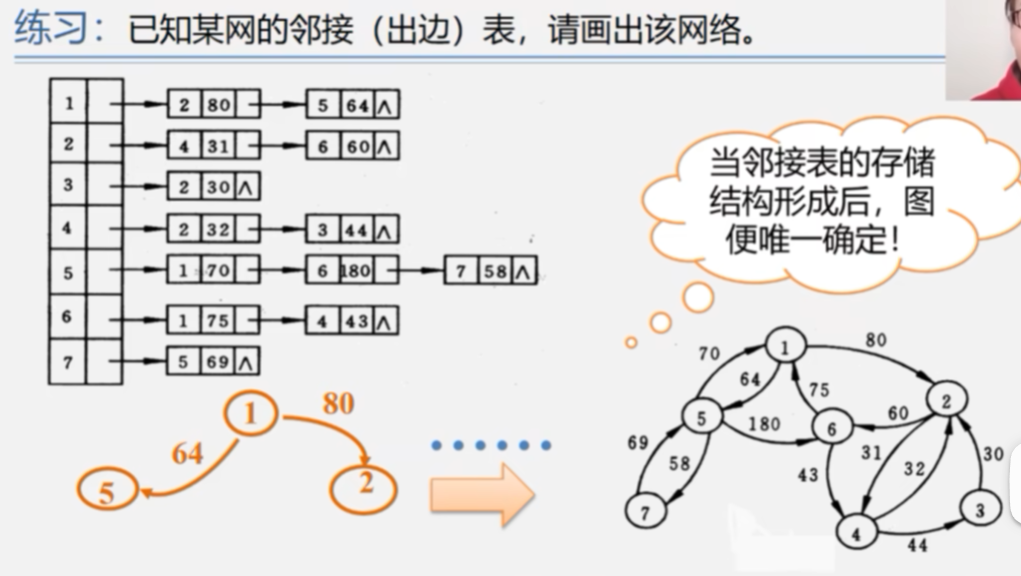
2.图的邻接表存储表示:
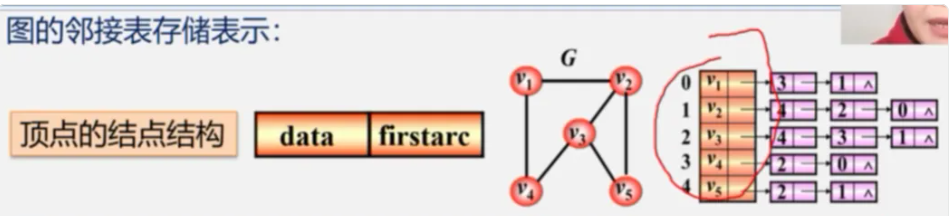
typedef struct VNode{
VerTexType data//顶点信息
ArcNode * firstarc;//指向第一条依附该顶点的边的指针
}VNode, AdjList[MVNum]; //AdjList表示邻接表类型
![]()

#define MVNum 100//最大顶点数
typedef struct ArcNode{//边结点
int adjvex;//该边所指向的顶点的位置
struct ArcNode * nextarc;//指向下一条边的指针
Otherlnfo info;//和边相关的信息
}ArcNode;

typedef struct {
AdjList vertices; //vertices--vertex的复数
int vexnum,arcnum;//图的当前顶点数和弧数
}ALGraph;
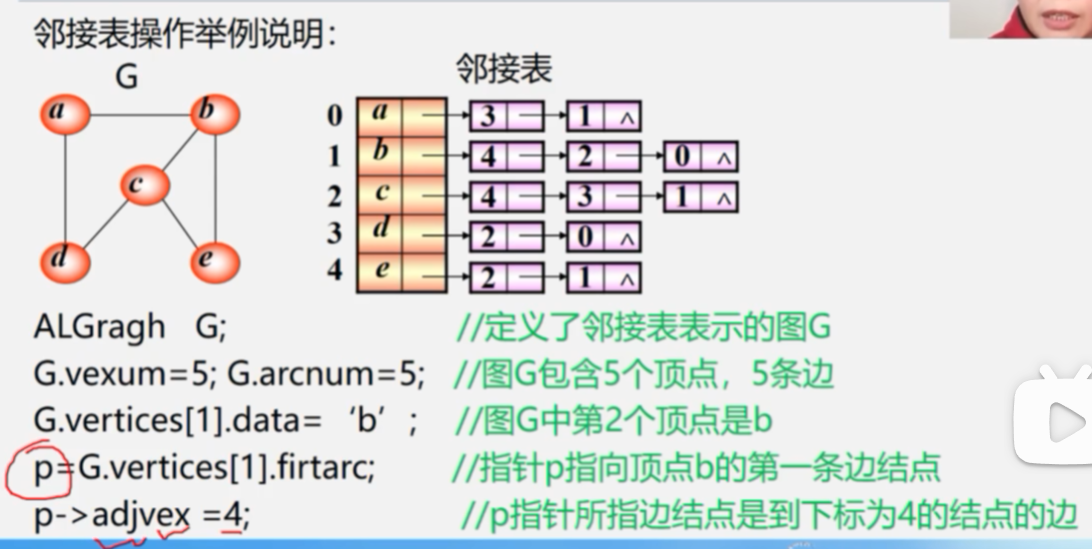
3.采用邻接表表示法创建无向网

算法6.2 采用邻接表表示法创建无向网
Status CreateUDG(ALGraph &G){ //采用邻接表表示法,创建无向图G
cin>>G.vexnum>>G.arcnum;//输入总顶点数,总边数
for(i = 0; i<G.vexnum; ++i){//输入各点,构造表头结点表
cin>> G.vertices[i].data;//输入顶点值
G.vertices[i].firstarc=NULL;//初始化表头结点的指针域
}//for
for(k = 0; k<G.arcnum;++k){//输入各边,构造邻接表
cin>>v1>>V2; //输入一条边依附的两个顶点
i= LocateVex(G, v1);
j= LocateVex(G, v2);
p1=new ArcNode;//生成一个新的边结点*p1
p1->adjvex=j;//邻接点序号为j
p1->nextarc= G.vertices[i].firstarc;
G.vertices[i].firstarc=p1;//将新结点*p1插入顶点vi的边表头部
p2=new ArcNode;//生成另一个对称的新的边结点*p2
p2->adjvex=i;//邻接点序号为i
p2->nextarc= G.vertices[j].firstarc;
G.vertices[j].firstarc=p2;//将新结点*p2插入顶点vj的边表头部
}//for
return OK;
}//CreateUDG
4.邻接表
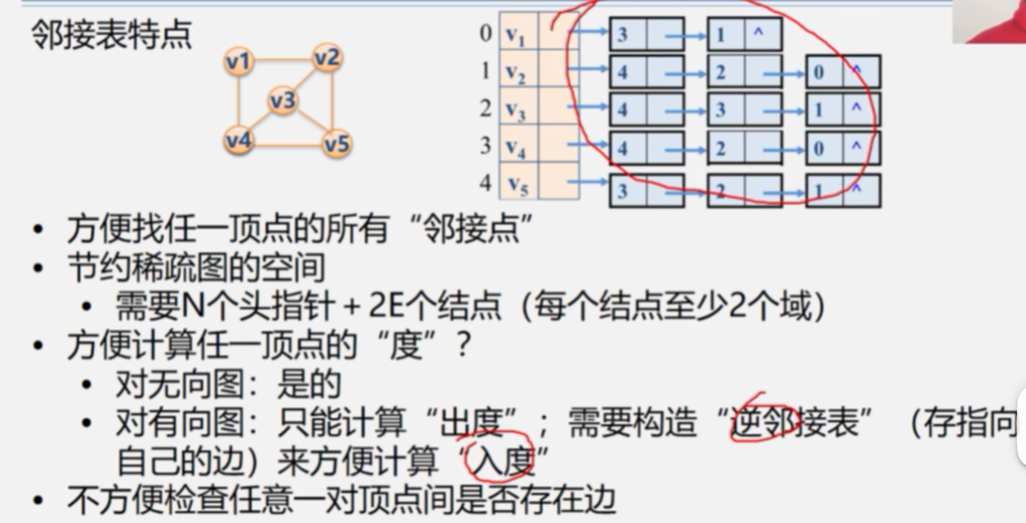
5.邻接矩阵与邻接表表示法的关系

6.图的存储结构

6.4.3十字链表--用于有向图

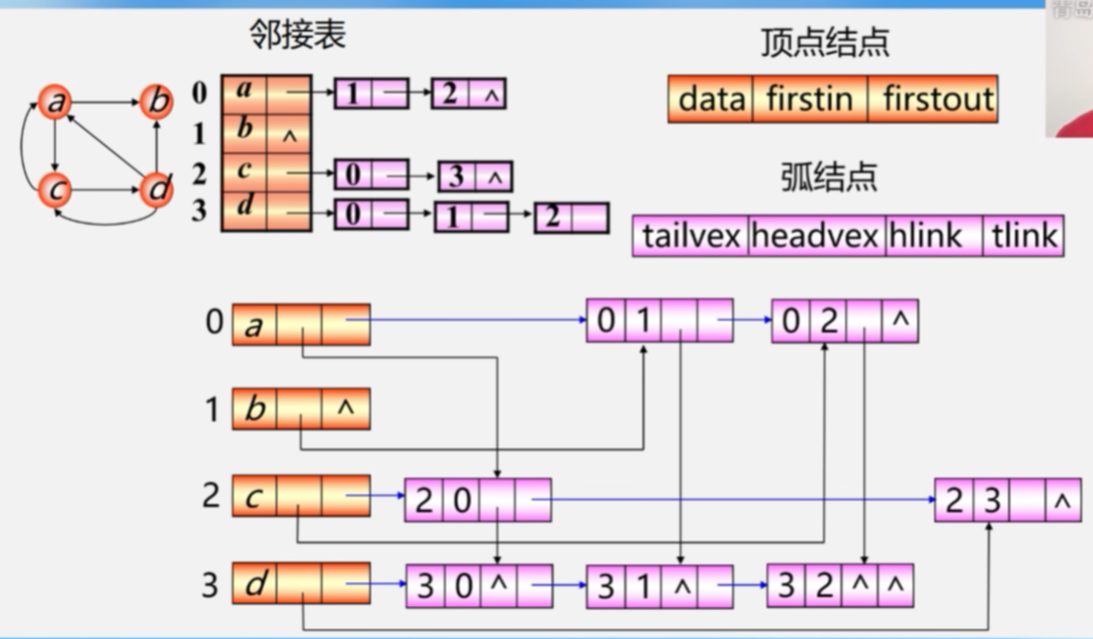
6.4.4邻接多重表(无向图的另一种链式存储结构)
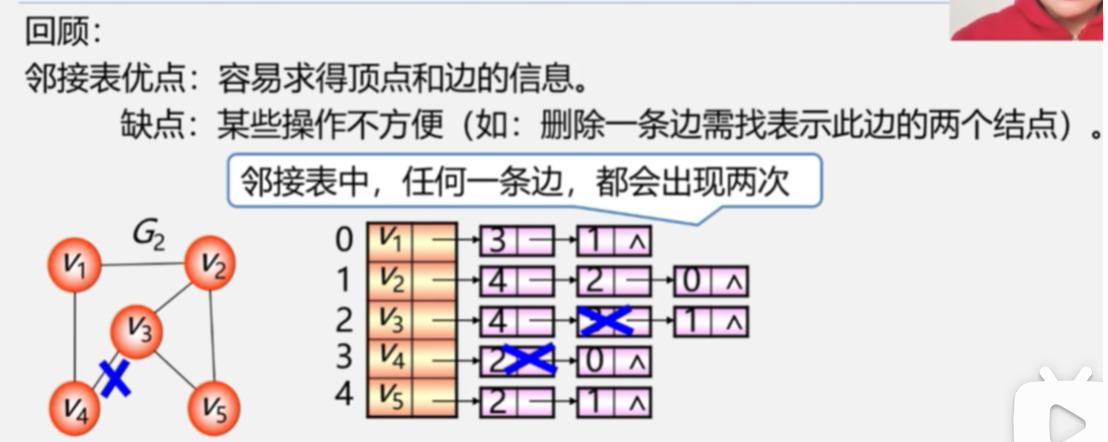
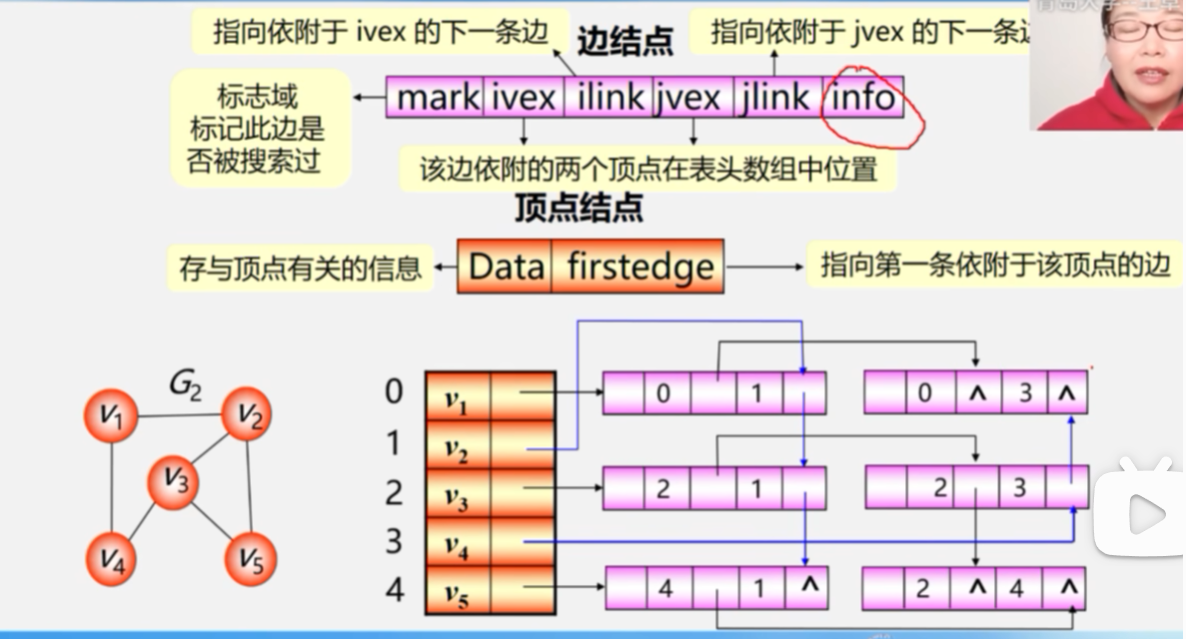
6.5图的遍历
1.遍历定义
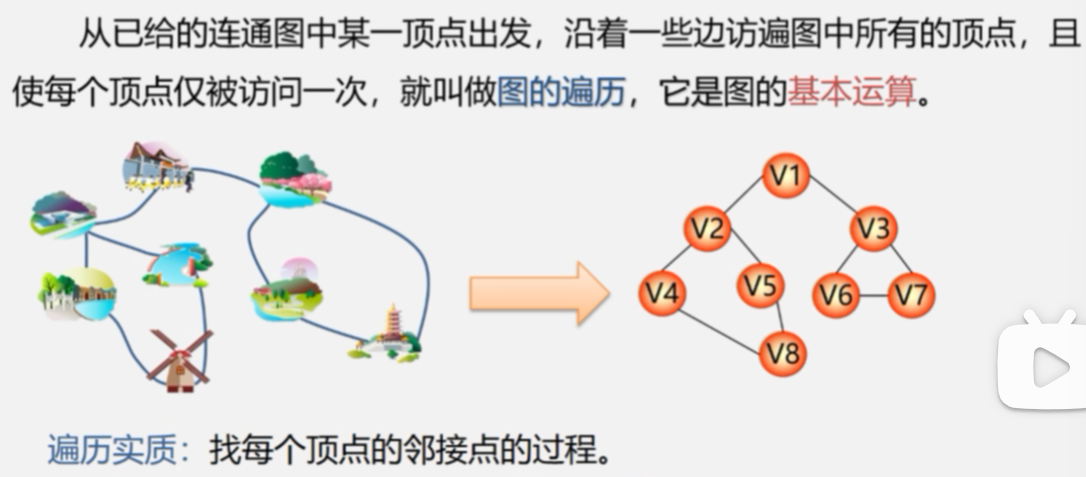
2.图的特点

3.图常用的遍历

4.深度优先遍历(DFS)
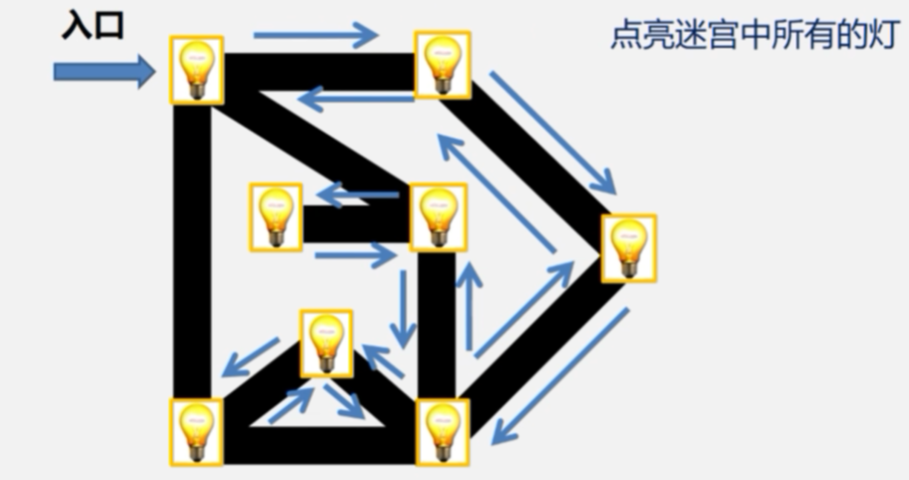


5.深度优先搜索遍历算法的实现
邻接矩阵表示的无向图深度遍历实现
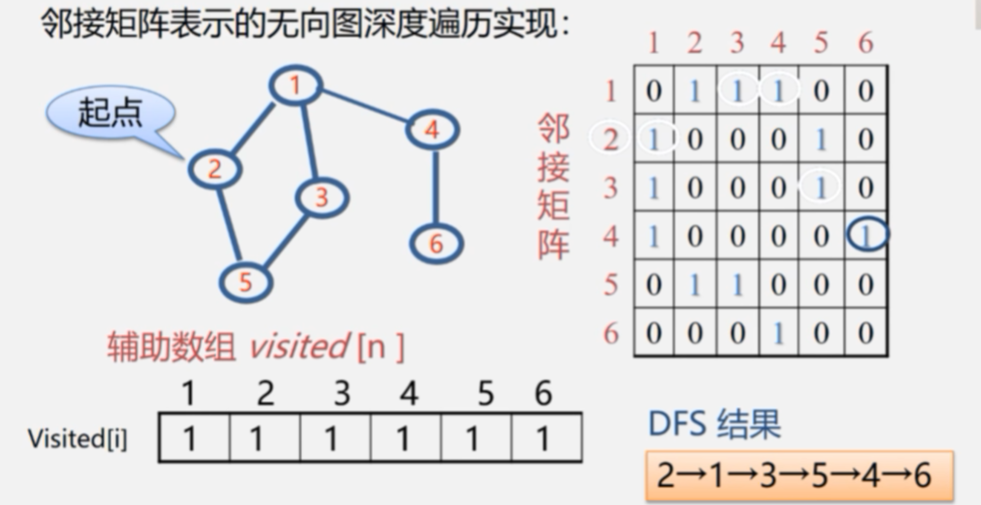
算法6.5 采用邻接矩阵表示图的深度优先搜索遍历
void DFS(AMGraph G, int v){//图G为邻接矩阵类型
cout<<v; visited[v] = true;//访问第v个顶点
for(w = 0; w< G.vexnum; w++)//依次检查邻接矩阵v所在的行
if((G.arcs[v][w]!=0)&& (!visited[w]))
DFS(G, w);
//w是v的邻接点,如果w未访问,则递归调用DFS
}
6.DFS算法效率分析

7.非连通图的遍历
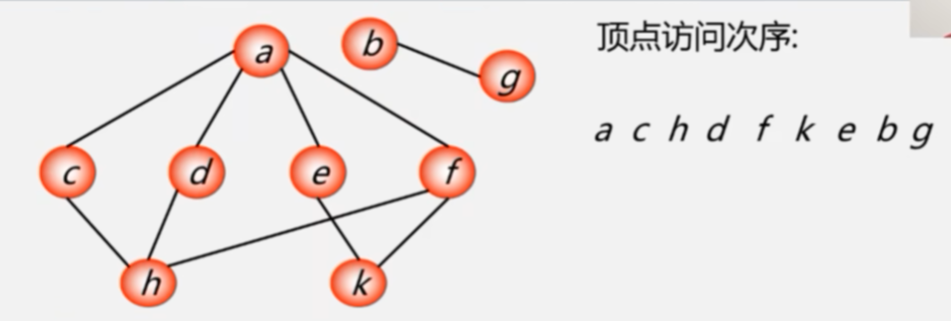
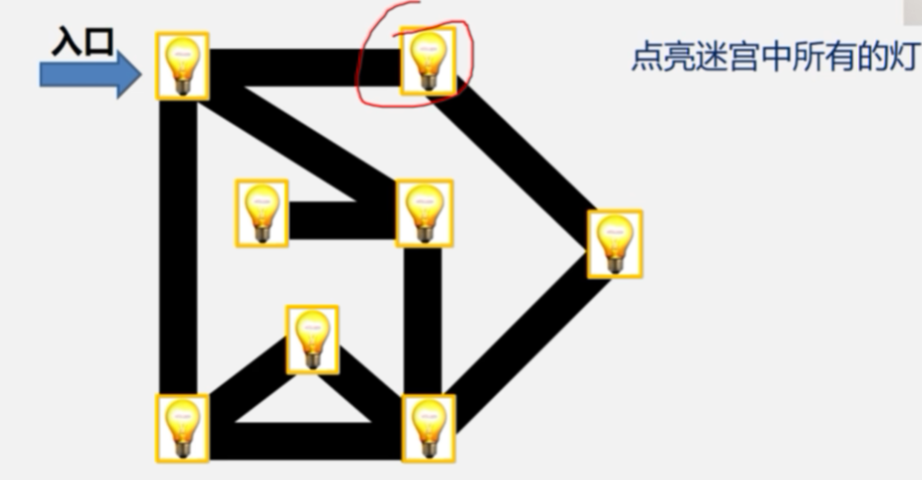
8.广度优先搜索(BFS-Breadth_First Search)

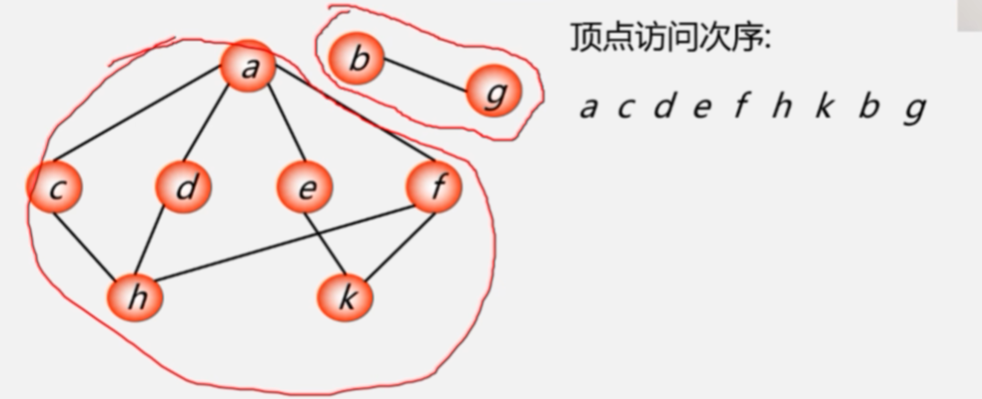
9.非连通图的广度遍历
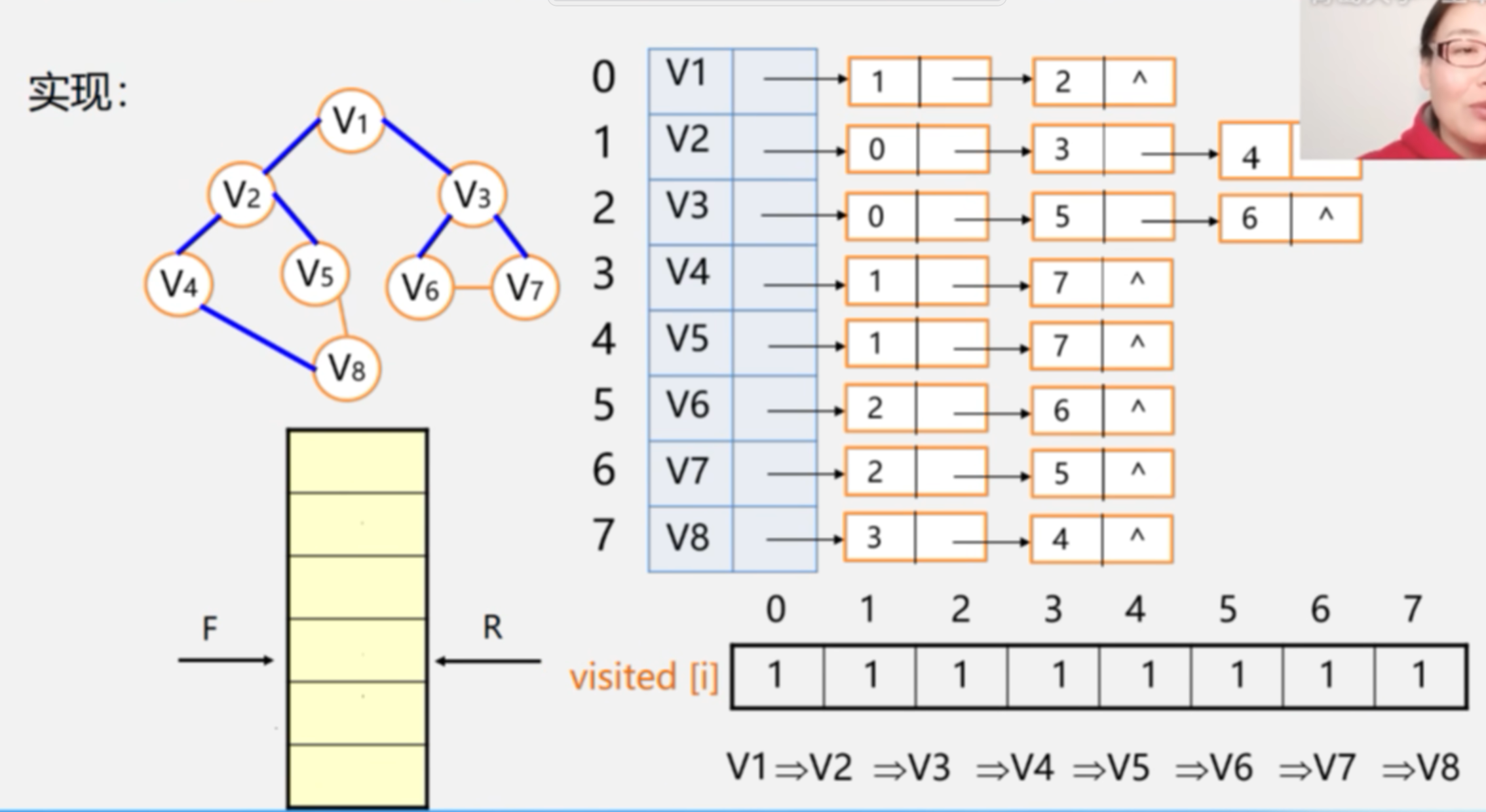
10.广度优先遍历
算法6.7 按广度优先非递归遍历连通图
void BFS (Graph G, int v) //按广度优先非递归遍历连通图G
cout<<v; visited[v] = true; //访问第v个顶点
InitQueue(Q); //辅助队列Q初始化,置空
EnQueue(Q, v); //v进队
while(!QueueEmpty(Q)){ //队列非空
DeQueue(Q, u); //从头元素出队并置为u
for(w = FirstAdjVex(G, u); w>=0; w = NextAdjVex(G, u, w))
if(!visited[w]){ //w为u的尚未访问的邻接顶点
cout<<"<w; visited[w] = true;" EnQueue(Q, w); //w进队
}//if
}//while
}//BFS
11.BFS算法效率分析

12.DFS与BFS算法效率比较

6.6图的应用

概念回顾---生成树
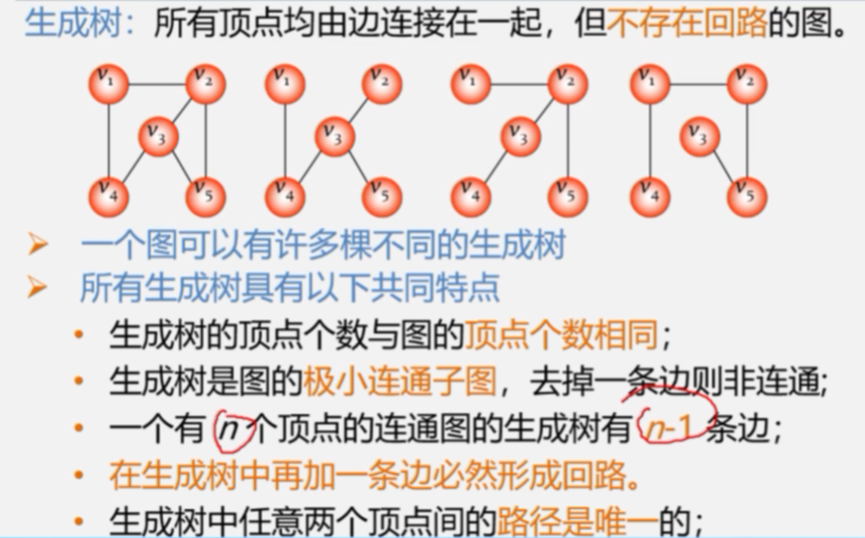
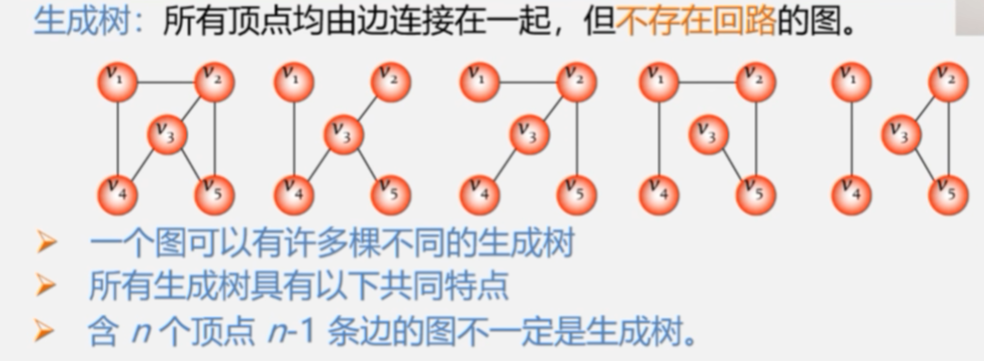
无向图的生成树
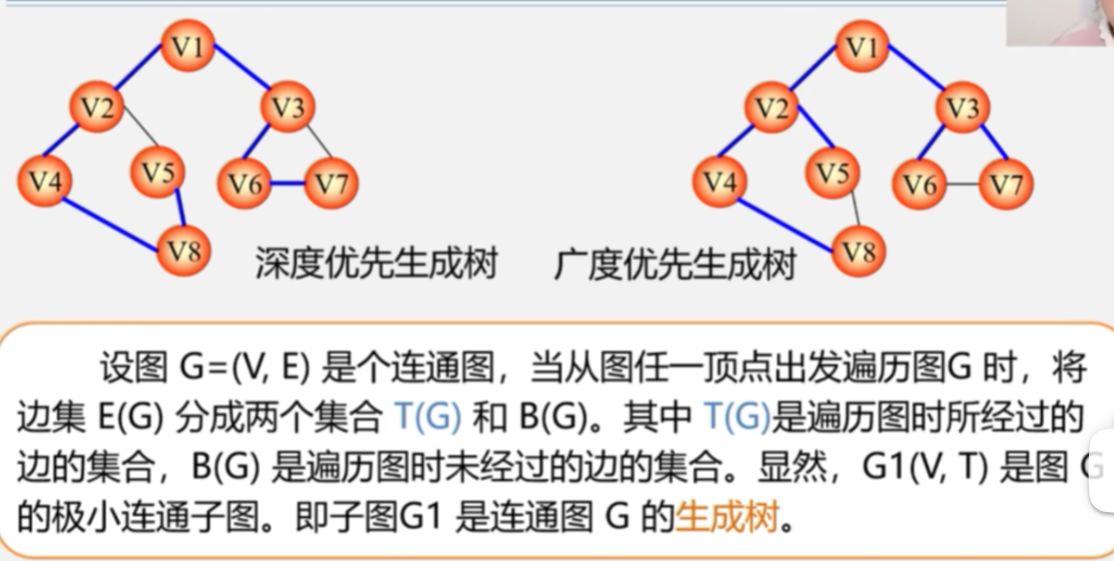
最小生成树
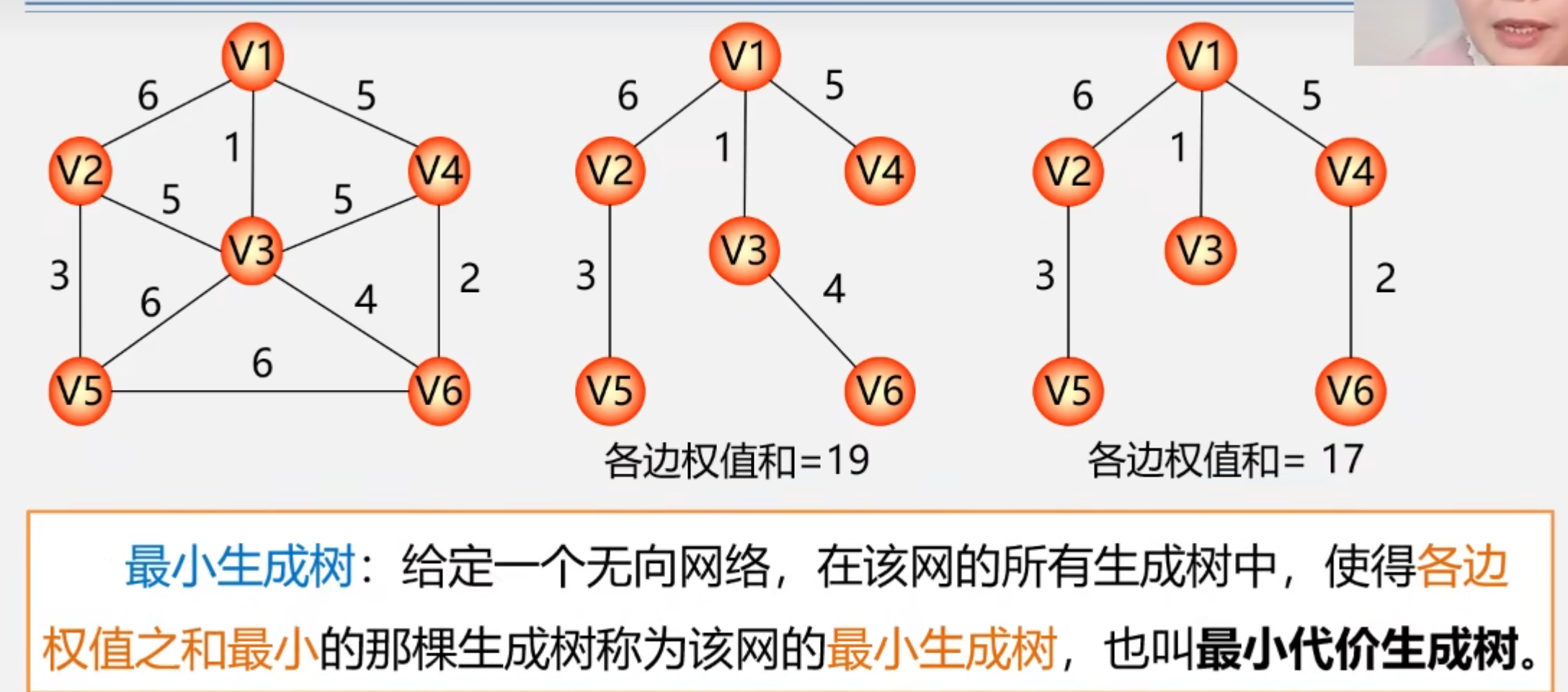
最小生成树的典型用途

构造最小生成树 Minimum Spanning Tree
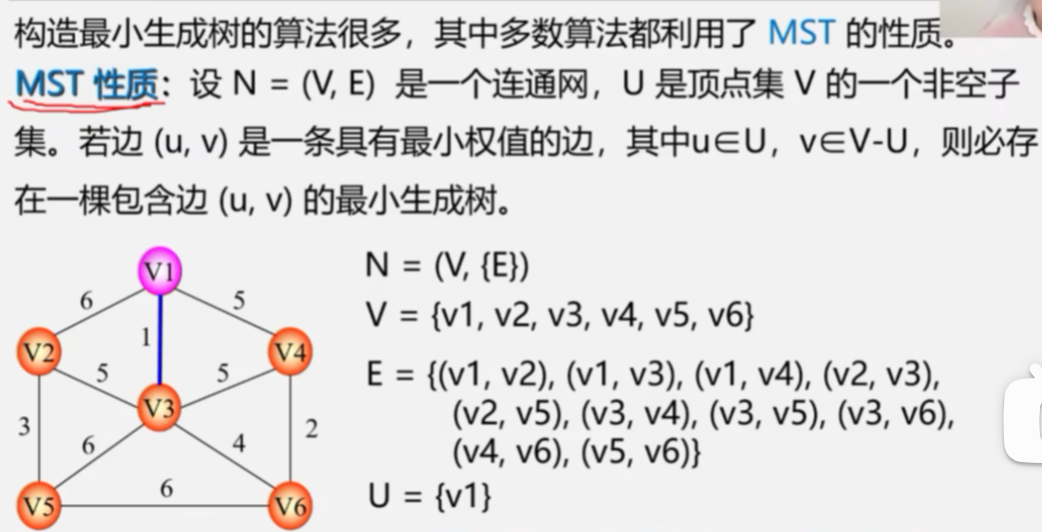
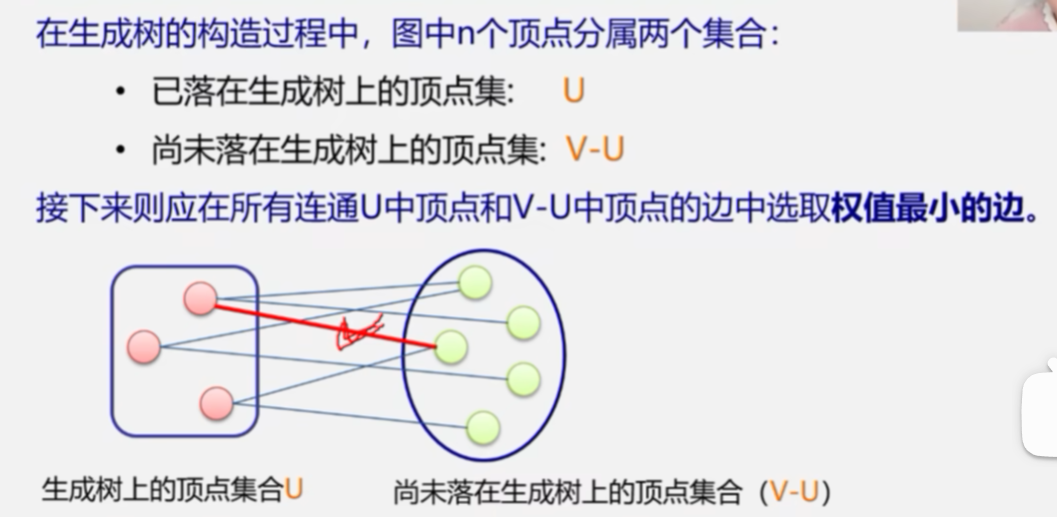
MST性质解释

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








