【自动控制原理】第四章根轨迹分析法

是Winky啊

于 2024-12-29 20:00:19 发布

阅读量646

点赞数 3

分类专栏：专业课文章标签：自动控制原理

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.youkuaiyun.com/Winkyyyyyy/article/details/144794074

版权

所谓分析，就是分析控制系统的三个基本要求：稳，准，快。

1. 根轨迹的基本概念及其两个基本条件

根轨迹定义：当开环传递函数中某个参数(往往是根轨迹增益 $K^*$ ) $0\rightarrow \infty$ 时，闭环特征根在 $s$ 平面上移动的轨迹。

增益的求解

增益的分类	求解方法
根轨迹增益	开环传递函数首一标准型，对应前面的系数 $K$
开环增益	开环传递函数尾一标准型，对应前面的系数 $K$
闭环增益	闭环传递函数尾一标准型，对应前面的系数 $K$

【计算题】已知系统正环传递函数为 $G(s)=\frac{4s-4}{s^{3}+3s^{2}+2s}$ ，求增益。

若要求根轨迹增益，化为首一标准型 $G(s)=\frac{4s-4}{s^{3}+3s^{2}+2s}=4\times \frac{(s-1)}{s(s^{2}+3s+2)}$ ，可得根轨迹增益为 $4$

若要求开环增益，化为尾一标准型 $G(s)=\frac{4s-4}{s^{3}+3s^{2}+2s}=\frac{4(s-1)}{2(\frac{1}{2}s^{3}+\frac{3}{2}s^{2}+s)}=2\times \frac{(s-1)}{\frac{1}{2}s^{3}+\frac{3}{2}s^{2}+s}$ ，可得开环增益为 $2$

根轨迹

【计算题】已知单位负反馈系统开环传递函数为 $G(s)=\frac{K_1}{s(s+8)}$ ，求 $K_1$ 从 $0\to\infty$ 变化时，系统的闭环根轨迹（由于是闭环传递函数分母解出来的根的轨迹，所以叫做闭环根轨迹）。

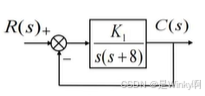
系统闭环特征方程（闭环传递函数分母）为 $s^{2}+8s+K_{1}=0$

特征根为 $s_{1,2}=-4\pm\sqrt{16-4K_{1}}$

随着参数变化变化根也在变化，根形成的轨迹就是根轨迹。

两个基本条件

根轨迹上的根一定满足的两个条件！

设控制系统如图所示，其特征方程为 $1+G(s)H(s)=0$

由闭环特征方程推出： $G(s)H(s)=-1$ （开环传递函数等于 $1$ ）

由于开环传函 $G(s)H(s)$ 是复数，可以用向量表示，将其分成两个方程。

⭐幅值条件(Angle condition)： $\begin{vmatrix}G(s)H(s)\end{vmatrix}=1$

⭐幅角条件(Magnitude condition)：

最低0.47元/天解锁文章

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。