算法题_位运算_3_二进制数中“1“比特的个数

位运算

二进制中1的个数

补充知识：>> 和 >>> 的区别
    1、>> 表示右移，如果该数为正，则高位补0；若为负数，则高位补1。如：int i=15; i>>2的结果是3，移出的部分将被抛弃；
    2、>>>表示无符号右移，也叫逻辑右移，即若该数为正，则高位补0，而若该数为负数，则右移后高位同样补0。   

题目：二进制中1的个数
题目描述：请实现一个函数，输入一个整数，输出该数二进制表示1的个数。
例如：9的二进制表示为1001，有2位是1

3.1、解法1

解法1：&运算
    1、拿到整数N的二进制数
    2、1左移i位(1<<i)，得到二进制数M
    3、若N & M == M, 则说明第i位是1
    	3.1、因为1的二进制表示中，只有一个1比特位，且1&1=1. 1&0=0
    	3.2、所以若第i为1，则会保留，其余比特&0=0
    4、遍历32次

public class 二进制中1的个数 {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int N = scanner.nextInt();
        System.out.println("十进制数：" + N);
        System.out.println("二进制数：" + Integer.toString(N, 2));

        //核心：&运算，1&1=1, 1&0=0, 0&0=0
        //解法1：
        //1、拿到N的二进制数
        //2、1向左移动i位 (1<<i)，得到二进制数M
        //3、若N&M == M ，则可说明N的第i位是1
        //4、遍历32次
        int count = 0;
        for (int i = 0; i < 32; i++) {
            if ((N & (1 << i)) == (1 << i)) {
                count++;
            }
        }
        System.out.println("(解法1) \"1\"比特的个数是：" + count);
    }
}

3.2、解法2

大体思路和解法1相同，只不过这个是N移位
解法2：&运算
    1、拿到N的二进制数
    2、N逻辑右移i位(N>>>i)，注意必须是逻辑右移，得到M
    3、N逻辑右移后的结果与1进行&运算，即 M & 1
    4、若 M & 1 == 1，则说明第i位是1

    ……
        //解法2：
        //1、拿到N的二进制数
        //2、N向右移动（注意是逻辑右移>>>）i位，得到M
        //3、N移位后的结果与1进行&运算，即M&1
        //4、若M&1 == 1，则可说明第i位是1
        count = 0;
        for (int i = 0; i < 32; i++) {
            if (((N >>> i) & 1) == 1) {
                count++;
            }
        }
        System.out.println("(解法2) \"1\"比特的个数是：" + count);
	……

3.3、解法3

解法3：&运算 和 -运算，消去所有的1，消去几次，即有几个1比特位
    1、(N-1) & N，即可消去N中最低位的1
    	1.1、N-1 可以消去N中最低位的1（若此位为x位），则会在x位后增加(x-1)个1
    	1.2、在 N-1 之后，我们在和N做&运算，即可，消去增加的1
    	1.3、因此，执行一次 (N-1) & N, 我们就可以消去一个最低的1
    2、循环执行步骤1，累计次数，直至N为0
    3、累计的次数就是1的个数
    
	……
        //解法3：利用 & 和 -
        //1、(N-1)&N，即可消去N中最低位的1
        //2、循环步骤1，直至N为0
        //3、循环的次数即为1的个数
        count = 0;
        while (N != 0) {
            N = ((N - 1) & N);
            count++;
        }
        System.out.println("(解法3) \"1\"比特的个数是：" + count);
    ……

---

调试结果：

---

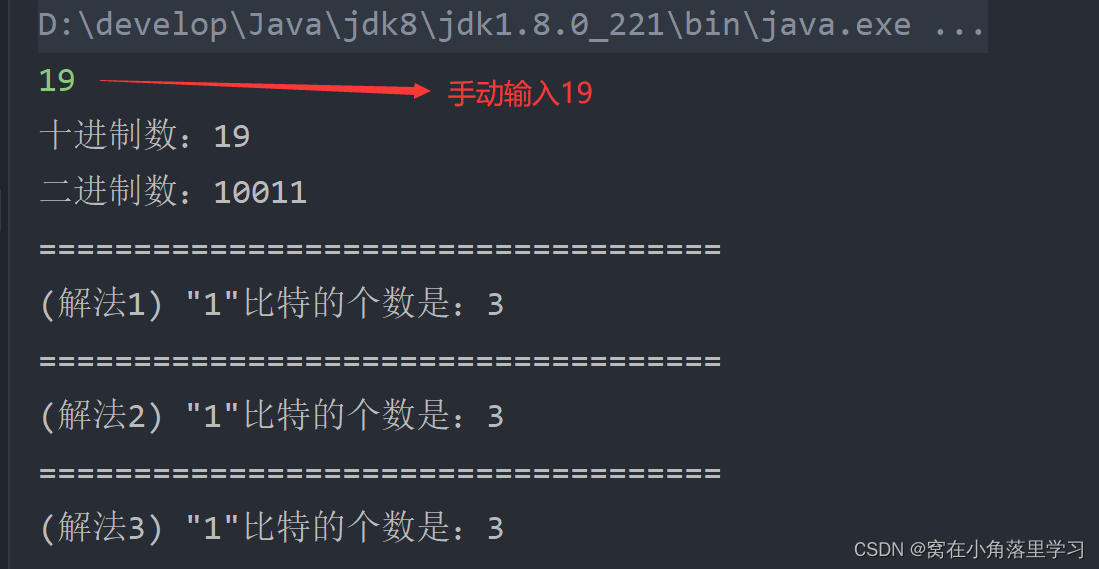
如有错误，敬请指正！