一、基础回顾
1.方差:刻画随机变量在其中心位置附近散布程度的数学特征,反映了随机变量取值的离散程度,常用的符号有σ²,s²,Var(X),D(X)等。
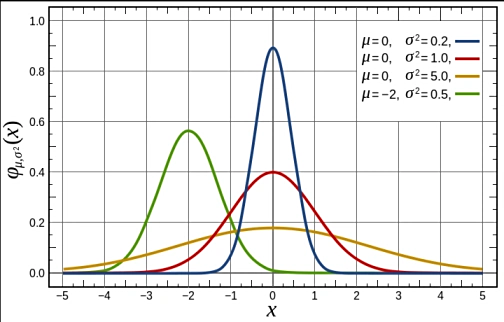 不同方差的正态分布
不同方差的正态分布
2.协方差:用来描述两个随机变量之间线性相关程度 [4],常用的符号有cov(X, Y),σ(X, Y)等
协方差 cov(X, Y) 定义为两个随机变量X和Y偏离其期望值的乘积的期望,即
cov(X,Y) = E[(X - E[X])(Y - E[Y])]
其中:E[X] 和 E[Y] 分别是随机变量 X 和 Y 的期望值, cov 是协方差的英文 “covariance” 的缩写。当协方差为正值时,表明随机变量X和Y倾向于同时偏离其平均值,呈正相关关系;反之,若协方差为负值,则表明一个变量高于平均值时,另一个倾向于低于平均值,呈负相关关系。如果协方差为零,这意味着两个变量之间没有线性关系。
相关系数r的定义:

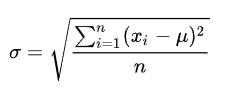
3.先验和后验:
先验是指在观察到任何数据之前,我们对某个事件或参数的 初始信念 或 初始概率。通常用 P(θ) 表示,其中 θ 是某个参数或事件。
后验是指在观察到数据之后,我们对某个事件或参数的 更新后的信念 或 更新后的概率分布。通常用 P(θ∣D) 表示,其中 D 是观察到的数据。 例如,在医疗诊断中,医生可能会根据以往的经验(先验)判断某种疾病的可能性,而在获得病人具体症状(后验)后,再调整这种判断。
二、卡尔曼滤波核心原理
卡尔曼滤波是一种用于线性系统状态估计的递归算法,核心价值在于融合 “系统预测模型” 与 “带噪声的测量数据”,输出最优的状态估计
适用场景
仅适用于线性系统(状态演化和测量过程均满足线性关系),且噪声服从零均值高斯分布(文档明确此为卡尔曼滤波 “最优性” 的前提)。若系统是非线性的(如无人机姿态控制),需使用其变体(扩展卡尔曼滤波 EKF、无迹卡尔曼滤波 UKF)。
七个核心公式:
1. 状态演化方程(预测系统状态)
描述 “系统在 t 时刻的状态如何从 t-1 时刻的状态演化而来”
![]()
| xt | t 时刻的状态向量(包含需估计的变量) |
| Ft | 状态转移矩阵(线性映射 t-1 时刻状态到 t 时刻的预测状态) |
| ut | 控制输入向量(外部对系统的干预,如油门、刹车) |
| Bt | 控制输入矩阵(线性映射控制输入到状态变化) |
| Bt | 控制输入矩阵(线性映射控制输入到状态变化) |
| wt | 过程噪声向量(零均值高斯分布,描述系统演化的不确定性) |
| Qt | 过程噪声的协方差矩阵(对角线为各状态的过程噪声方差,非对角为协方差) |
2. 测量方程(关联状态与观测)
描述 “传感器的测量值如何由系统真实状态生成”
![]()
| zt | t 时刻的测量向量(传感器输出值) |
| Ht | 测量矩阵(线性映射系统状态到测量域,解决 “状态与测量单位 / 维度不匹配”) |
| vt | 测量噪声向量(零均值高斯分布,描述传感器误差) |
| Rt | 测量噪声的协方差矩阵(对角线为各测量的噪声方差) |
3.卡尔曼滤波算法流程:预测与更新两大阶段
阶段1:预测(基于历史估计,推测当前状态)
目标:利用 t-1 时刻的最优估计,预测 t 时刻的 “先验状态”(未融合当前测量前的状态),同时计算该先验状态的不确定性(协方差)。
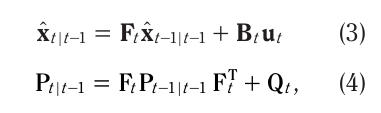
- Pt∣t−1 : t 时刻未融合当前测量数据时,状态预测的不确定性矩阵(先验协方差矩阵),表明当前预测数据的不确定性。在这个矩阵中,对角线上的元素表示各自状态的不确定性,协方差越大不确定性越大;非对角线上的协方差表示两个不同状态之间的关联程度。
例如;状态向量 xt=[xt,x˙t],包含 “位置” 和 “速度” 两个状态),可更直观理解非对角线元素的意义:该实例中协方差矩阵为 2×2 结构,形式如下:
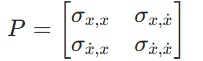
- 对角线元素 σx,x(位置方差)、σx˙,x˙(速度方差):分别表示位置、速度各自估计的不确定性(数值越大,该状态估计越不可靠);
- 非对角线元素 σx,x˙(位置与速度的协方差)、σx˙,x(速度与位置的协方差,因协方差矩阵对称,二者数值相等):表示 “位置估计误差” 与 “速度估计误差” 之间的关联程度。
- Pt∣t是 t 时刻融合当前测量数据后,状态最优估计的不确定性矩阵(后验协方差矩阵)。它是在 “更新阶段” 计算的,结合了 t 时刻的先验预测(Pt∣t−1)和当前传感器测量数据,是 t 时刻最终的不确定性量化结果。
阶段2:估计:更新(融合当前测量,得到最优估计)
先计算卡尔曼增益K,再根据K更新当前结合了预测和测量的最优估计值xt|t:
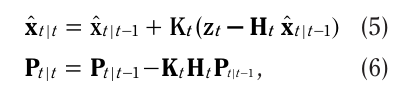
![]()
关键项解释:
- zt−Htx^t∣t−1:残差(Innovation),即 “测量值与‘先验状态映射到测量域的值’的差值”;
- 若残差为 0:预测与测量完全一致,无需调整;
- 若残差不为 0:通过Kt加权调整先验状态,得到最优后验状态。




















 6万+
6万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








