《画解数据结构》二十五彩图，画解平衡二叉树

前言

  上一篇文章 「 二叉搜索树 」 中，对于 「 增 」「 删 」「 改 」「 查 」 的时间复杂度为 $O(lo{g}_{2}n)$ ~ $O(n)$。原因是最坏情况下，二叉搜索树会退化成 「 线性表 」 。更加确切地说，树的高度决定了它插入、删除和查找的时间复杂度。
  本文，我们就来聊一下一种高度始终能够接近 $O(lo{g}_{2}n)$ 的 「 树形 」 的数据结构，它既有链表的快速插入与删除的特点，又有顺序表快速查找的优势。它就是：

「 平衡二叉树 」

来个右旋压压惊
来个左旋压压惊

一、平衡二叉树的概念

1、定义

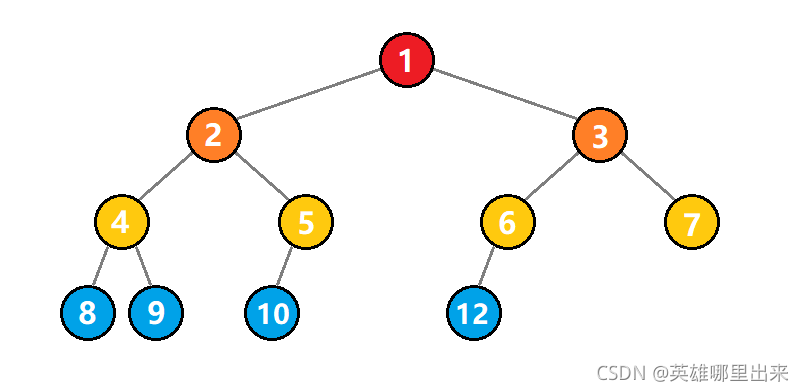
  平衡二叉树 是 二叉搜索树 的一种。之所以平衡，是因为它的每一个结点的 左子树的高度 和 右子树的高度 差至多为 1。如图所示，代表的是一棵平衡二叉树，其中数字代表的是结点的编号。

  1962年，两位俄罗斯数学家 G.M.Adelson-Velskii 和 E.M.Landis 共同发明了一种解决平衡二叉树的算法，所以后面也有不少资料称这种平衡二叉树为 AVL 树。
  而至于为什么不叫 二叉平衡树，而叫平衡二叉树 ？因为它首先是 二叉搜索树，并且是平衡的二叉搜索树，所以省略 “搜索” 二字以后，就有了 平衡二叉树 的叫法。

2、高度

  一棵树的高度，是指从树根结点到达最远的叶子结点的路径上经过的结点数。
  所以，求树的高度我们可以采用递归的方式。主要有以下三种形式：
  1）空树的树高为 0；
  2）叶子结点的树高为 1；
  3）其它结点的树高，等于左右子树树高的大者加 1；
  如图所示，每个结点右上角的数字代表了以它为子树的高度。