汇编语言（2）---数在计算机中的表达

整数在计算机的表达和运算

数制
x86 1 Word = 2Byte=16 bits MIPS 1 Word = 4 Byte = 32 bits
数制之间的转换

逻辑运算
数的机器表示（初步）
机器字长（machine word）：
一般指计算机进行一次整数运算算处理的二进制数据的位数

• 通常也包括数据地址的长度

32位字长

• 地址的表示空间是4GB
• 对很多内存需求量大的应用而言，非常有限

64位字长

• 地址的表示空间约1.8*$10^{19}$bytes
• 目前的x86-64机型实际支持48位宽的地址：256TB

机器字在内存中的组织
地址按照字节（byte）来定位
机器字中第一个字节的地址
相邻机器字的地址相差4（32-bit）或者8（64-bit）

一个机器字内的各个字节如何排列?
大端/小端（big endian/little endian）
big endian：PowerPC Internet
little endian：x86 ARM

（和性能无关，只是排列问题）
整数表示
int是一样的， long是不一样的 指针不一样

计算机表示整数
w 表示机器字长
无符号数和带符号数
int 无符号 w=32时，
正常原码表示

unsigned int 带符号 补码表示
有正负 和零
例如short
最高位表示符号位 表示$-2^{16}$
按位取反+1
原码 0011 0000 0011 1001
反码 1100 1111 1100 0110
+1
补码 1100 1111 1100 0111

无符号取值范围
0 ~ $2^w$-1

有符号数范围

TMin = -$2^{w-1}$
1000…000
TMax = $2^{w-1}$-1
0111…111
Other values
-1 = 111111…1111

（重点）无符号数与带符号数之间的转换，二进制串的表示是不变的。
（计算机硬件看不到带不带符号，C语言层面有没有符号是有区别的，这个区别谁来做？？？）

常数（constants）

• 默认是带符号数
  如果有“U”作为后缀则是无符号数，如0U， 4292432423U
  如果无符号数与带符号数混合使用，则带符号数默认转换为无符号数
  注意：-1 与0U
  -1 表示为1111111111
  0表示为000000000

何时采用无符号数？

• 模运算
• 按位运算

sizeof 返回 unsigned int
都转unsigned 永远 >= 0

尽量使用有符号数

如果加法有进位，进位被踢掉。可能产生溢出。结果模$2^w$
C语言不检测溢出。写程序注意。

补码加法
和之前一样，汇编只有add

溢出情况
两个正数相加 之后是负数
两个负数相加 之后是正数
（溢出不检测）
电路层面除法
整数 加减乘简单，除法难
尽量避免除法
逻辑右移k位 除以$2^k$
C整数除法，小数点后一刀切 没有四舍五入
无符号整数 移出去就移出去了

逻辑右移补0 算数右移补符号位（0或1）

带符号数 右移有问题
往小舍入 参考上图第二例。
加入一个矫正 +一个$2^k$-1

浮点数的机器表示

IEEE浮点数 IEEE754
IEEE Floating Point
整数小数点放最右侧，小数把小数点放中间
浮动的点，小数点。
定点表示实数？？？（回去想）
s是符号位，和整数不同，这个是真的符号位，0表示正数，1表示0

浮点数的类型

• 规格化浮点数（Normalized）
  除了s之外，另外两个域做了转换
  （记住）
  float 127
  double 1023
  min 00000000 1.0
  max 11111111 2.0-e
  
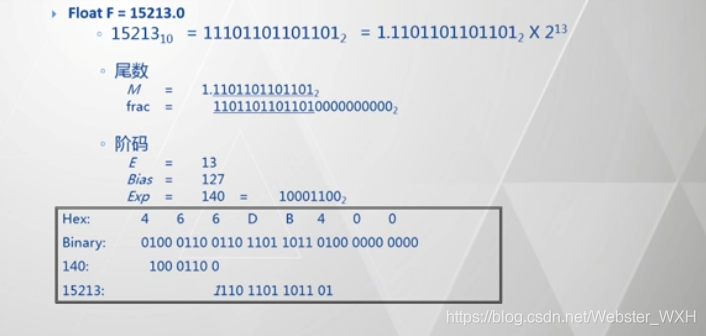
• 非规格化浮点数（Denormalized）
  - 一些特殊值
  

浮点数表示的特性

各种浮点数类型在数轴上的相对位置
不看符号位，和整型比较大小是一样。

Rounding （舍入）

给定一个实数，如果给出其浮点数表示？
保证最低有效数位是偶数（计算机内部默认）

C语言中的浮点数