数据结构与算法：二叉排序树与平衡性
文章讨论了二叉排序树的平衡性问题，指出树高最小的二叉排序树最优。还涵盖了数据结构的基本概念，如数据元素、逻辑结构和物理结构。此外，提到了栈的操作、哈夫曼编码的特点、循环队列的空间溢出问题以及KMP算法的匹配效率。文章还涉及其他算法和数据结构，如链表、哈希表和二叉树的相关性质。
一.判断题
N个结点的二叉排序树有多种，其中树高最小的二叉排序树是最佳的。T
这里考察的是树的平衡性问题，平衡树的构造就在于左右子树的均匀分配，降低树的高度，所以树高越小的排序树越好
数据的逻辑结构是指数据的各数据项之间的逻辑关系。F
应为数据元素，数据元素包含数据项
n个元素通过一个栈产生n个元素的出栈序列，其中进栈和出栈操作的次数总是相等的。T
# 设有n个元素按顺序进栈，问出栈有多少种情况
n个不同元素进栈，出栈元素不同排列的个数为：卡特兰数公式
有n个数存放在一维数组A[1..n]中，在进行顺序查找时，这n个数的排列有序或无序其平均查找长度不同。F
一棵有124个结点的完全二叉树，其叶结点个数是确定的。T
二叉树节点数：总数=N0+N1+N2,No为叶节点数，N1为有一个子节点的节点，其中N0=N2+1
数据结构包括数据对象集以及它们的逻辑结构和物理结构，还包括与数据对象相关联的操作集，以及实现这些操作的高效的算法。T
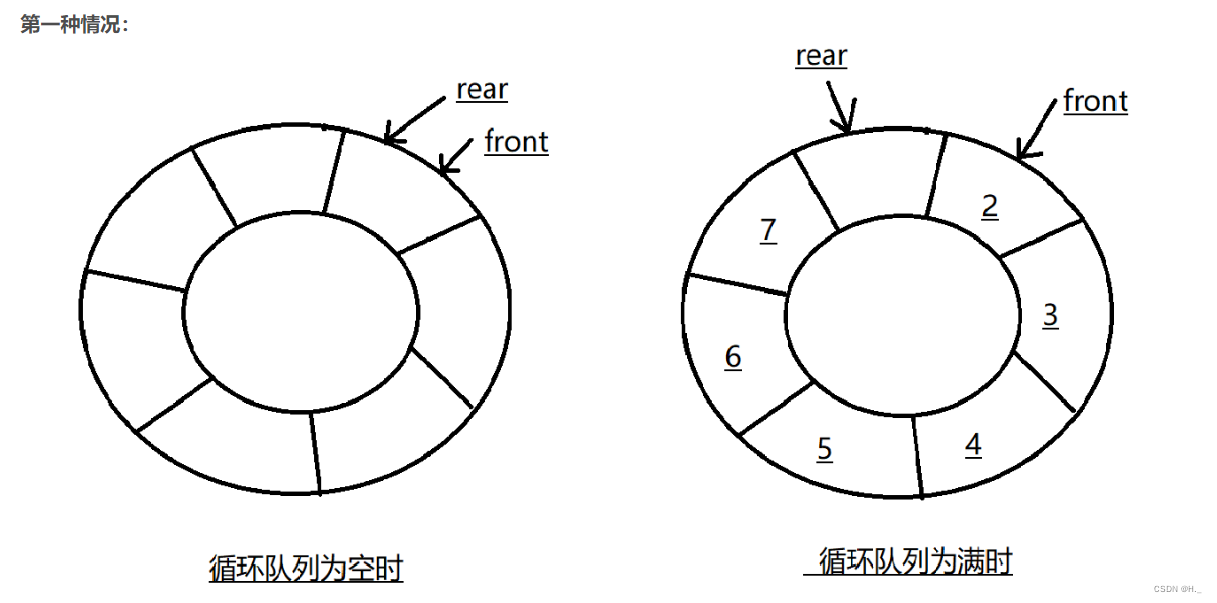
循环队列也存在空间溢出的问题。T
分析：循环队列解决的是“假溢出”问题，但是仍然出现真正的溢出问题。假溢出指的是下标溢出，真溢出指的是空间溢出。
循环队列面临着数组可能溢出的问题。
链表的每个结点都恰好有一个指针。F
错误。链表中的结点可含多个指针域，分别存放多个指针。例如，双向链表中的结点可以含有两个指针域，分别存放指向其直接前趋和直接后继结点的指针。
KMP算法的最大特点是指示主串的指针不需要回溯。T
KMP算法是一种用于字符串匹配的算法，其全称为Knuth-Morris-Pratt算法。KMP算法的核心思想是避免重复匹配已经匹配过的字符，从而使得字符串匹配的效率得到提升。在KMP算法中，首先构造出一个状态转移图，通过状态转移图来确定匹配的位置，然后扫描目标串和模式串，根据状态转移图来进行匹配，从而实现在目标串中查找模式串的功能。
KMP算法的关键在于构造状态转移图，该图能够根据模式串中已经匹配过的字符，快速确定下一次匹配的起始位置。具体而言，KMP算法会预处理出一个长度与模式串相等的next数组，next[i]表示当第i个字符失配时，应该从哪里开始继续匹配，这样就可以把匹配过程中的回溯情况消除，提高了匹配的效率。
在哈夫曼编码中，当两个字符出现的频率相同时，其编码也相同，对于这种情况应特殊处理。F
哈夫曼树中 两个频率相同的字符不会有相同的哈夫曼编码，除非它们是相同的字符。
在任意一棵非空二叉排序树中，删除某结点后又将其插入，则所得二排序叉树与原二排序叉树相同。F
没有说明是叶节点,叶节点正确
算法独立于具体的程序设计语言，与具体的计算机无关。T
算法和程序没有区别，在数据结构中二者是通用的。F
算法（Algorithm）通常指的是一种解决问题的方法或者过程，是一个抽象的概念，描述的是完成某个任务所需要的步骤和规则，而不是具体的实现代码。在计算机科学中，算法是研究如何用最少的时间和空间复杂度来解决问题的重要分支。
程序（Program）是一组指令的集合，是算法的具体实现形式，是一种计算机语言的表现形式，用特定的语法和结构描述出解决问题的步骤和规则。
关于哈夫曼树和完全二叉树：哈夫曼树一定是完全二叉树。F
哈夫曼树是指一种带权路径最小的树，即权值较大的节点离根节点较近，权值较小的节点离根节点较远。哈夫曼树的构造过程是通过不断合并权值最小的两个节点来实现的。
在哈夫曼树的构造过程中，每次合并都会形成一个新的节点，因此哈夫曼树并不一定是完全二叉树。当然，如果给定的节点序列能够形成完全二叉树，那么构造出的哈夫曼树也就是完全二叉树了。
实际上，为了保证哈夫曼树的带权路径最小性质，我们只需要满足在每一步合并时选择的两个节点中，权值较小的节点作为父节点，权值较大的节点作为子节点即可，而不需要考虑节点的位置关系。这意味着哈夫曼树可以是任意形态的二叉树。
给定两个排序列表L1和L2，计算L1并L2的最快算法的时间复杂度为Θ(N^2) F
最快为O(N)
在N个结点的顺序表中访问第i（1<=i<=N）个结点和求第i（2<=i<=N）个结点直接前驱的算法时间复杂度均为O(1)。T
顺序表-数组，有下标，随机存储和访问，时间复杂度为O(1)
两个栈共享一片连续空间，可以将两个栈的栈底分别设在这片空间的两端。 T
二叉树中除叶结点外, 任一结点X，其左子树根结点的值小于该结点（X）的值；其右子树根结点的值≥该结点（X）的值,则此二叉树一定是二叉排序树。F
二叉排序树的形态可以为空树
一棵非空二叉树，若先序遍历与后序遍历的序列相反，则该二叉树只有一个叶子结点。F
可能的情况有：
在一个设有头指针和尾指针的单链表中，执行删除该单链表中最后一个元素的操作与链表的长度无关。F
删除最后一个元素需要知道其前驱结点，使前驱结点的指针指向NULL，而仅有头尾指针的单链表想要访问到最后一个元素的前驱结点依旧需要从头到尾顺序访问，所以有关。
可以通过少用一个存储空间的方法解决循环队列中队空和队满条件的区分。 T
若一搜索树（查找树）是一个有n个结点的完全二叉树，则该树的最小值一定在叶结点上。F
在左子树最左的叶结点处
稀疏矩阵压缩存储后，必会失去随机存取功能。T
稀疏矩阵在采用压缩存储后将会失去随机存储的功能。因为在这种矩阵中，非零元素的分布是没有规律的，为了压缩存储，就将每一个非零元素的值和它所在的行、列号做为一个结点存放在一起，这样的结点组成的线性表中叫三元组表，它已不是简单的向量，所以无法用下标直接存取矩阵中的元素。
《数据结构》是一门研究非数值计算的程序设计问题的学科 。T
F ；
二叉搜索树中最大的元素必须在根的右子树中。T
算法的优劣与算法描述语言无关，但与所用计算机有关。F
算法优劣主要由算法自身的时间复杂度和空间复杂度决定，跟使用哪种程序语言描述无关，也跟在何种性能计算机上执行无关。
数据元素可以由类型互不相同的数据项构成。T
线性表的插入、删除总是伴随着大量数据的移动。F
线性表有数组，有链表
任一查找树(二叉分类树)的平均查找时间都小于用顺序查找法查找同样结点的线性表的平均查找时间.F
二叉树的最坏情况为O(N)级，为非平衡二叉树时
用一维数组存储二叉树时，总是以前序遍历顺序存储结点。F
运用层序遍历
在查找树（二叉树排序树）中插入一个新结点，总是插入到叶结点下面。F
按插入后中序遍历是递增序列的原则，若某结点只有右子树，而插入元素的关键字小于该结点的关键字，则会插入到该结点的左侧，成为其左孩子。这种插入就不是插入到叶子下面。
抽象数据类型与计算机内部表示和实现无关。T
非空线性表中每个结点都有一个前驱结点。F
头节点没有前驱结点
哈夫曼树的结点个数不能是偶数。T
哈夫曼树的结点个数不能是偶数 而根据二叉树的一个基本特点，度为0的结点总是比度为2的结点多一个，设度为2的结点有n个，那么霍夫曼树的总结点就是2n+1个，n为自然数。 显然2n+1是奇数，因此霍夫曼树的结点个数不可能是偶数。
采用顺序存储结构的循环队列，出队操作会引起其余元素的移动。F
明显不对，顺序循环队列，根本就不涉及元素移动！只是front与rear在移动！ 错误！
在选择数据对象的存储结构时，主要考虑该对象有哪些运算、节点的多少以及所采用的编程语言是否适合实现这种结构，不必考虑数据对象中各元素的取值。T
二叉树可以用二叉链表存储，树无法用二叉链表存储。F
设深度为d（只有一个根结点时，d为1）的二叉树只有度为0和2的结点，则此类二叉树的结点数至少为2d-1
抽象数据类型中基本操作的定义与具体实现有关。F
广义表是一种多层次的数据结构，其元素可以是单原子也可以是子表。T
对一棵二叉排序树按前序方法遍历得出的结点序列是从小到大的序列。F
中序遍历才是
扫一扫
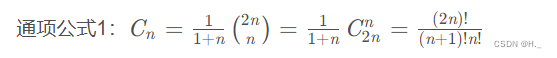
1524
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
