货车运输（python）

最新推荐文章于 2024-12-23 00:23:25 发布

数学人学python

最新推荐文章于 2024-12-23 00:23:25 发布

阅读量397

点赞数 3

CC 4.0 BY-SA版权

文章标签：数据结构

本文链接：https://blog.youkuaiyun.com/W_extend/article/details/137511887

文章介绍了如何使用Prim算法和Kruskal算法生成最大树，以解决查询路径最大承载力的问题。通过LCA优化，查询效率大大提高。Trie结构用于存储和操作数据，有助于降低查询复杂度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

看见数据范围知，只能使用小于（nlogn）的算法。

询问x到y的最大载重，意思为从x到y开车，这条路径需要在所有从x到y的路径中的最小值，让最小值最大，考虑生成最大树，从已知相连接的两点之间，只选择路径最大的那条，生成一棵树，那么从x到y，就算绕路走，也走最大的那唯一的一条路。

目前有prim（时间复杂度mlogn）和kru（时间复杂度mlogm）两种算法生成最大树。(m为边的数量，n为点的数量），不知道为啥这题选kru？我也不知道

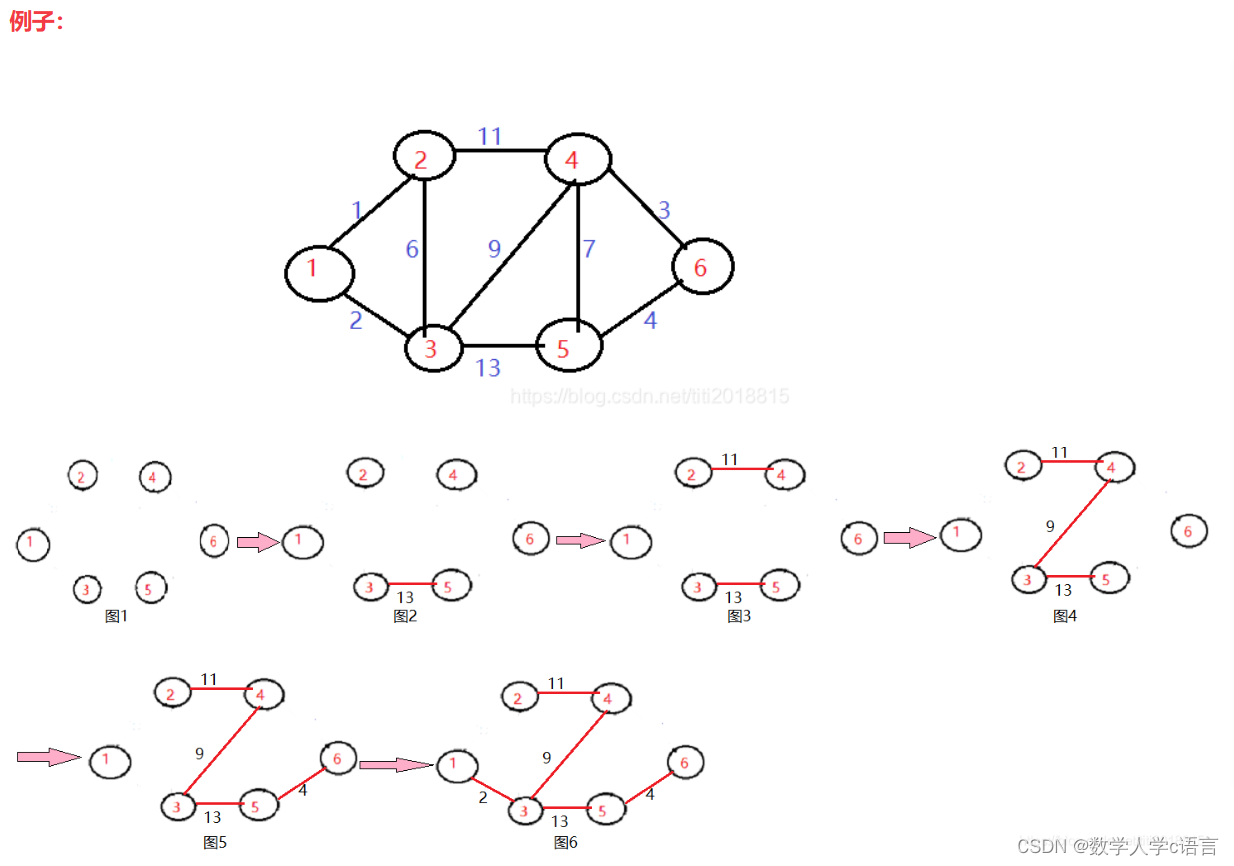生成最大树后，如果查询q次最大承载力，暴力的算法可能复杂度达到qn，所以使用LCA优化寻找速度，例如查（1,2**10+2）的最大承载力，可以先查（1,2**10）再查（2**10,2**10+2）。

洛谷可以ac，acwing报错。

from collections import defaultdict, deque

class trie:
    def __init__(self, value):
        self.v = []
        for i in range(n+1):
            self.v.append(i)
        self.edge = defaultdict(dict)
        self.leth = value
        self.f = [ [0]*20 for _ in range(n+1) ]
        self.w = [ [0]*20 for _ in range(n+1) ]
        self.d = [0]*(n+1)
        
    def add_path(self, x, y, w):
        x1 = self.find_father(x)
        y1 = self.find_father(y)
        if x1 != y1:
            self.leth -= 1
            self.v[x1] = y1
            self.edge[x][y] = w
            self.edge[y][x] = w
        if not self.leth:
            return True

        
    def find_father(self, x):
        if self.v[x] == x:
            return x
        self.v[x] = self.find_father(self.v[x])
        return self.v[x]
    
    def create(self):
        self.vis = [0]*(n+1)
        for i in range(1, n+1):
            if self.vis[i] == 0:
                self.dfs(i,0)
    
    def dfs(self, now, fa):
        self.vis[now] = 1
        self.f[now][0] = fa
        if fa == 0:
            self.w[now][0] = float('inf')
        else:
            self.w[now][0] = self.edge[now][fa]
        self.d[now] = self.d[fa] + 1
        
        for i in range(1, 20):
            self.f[now][i] = self.f[self.f[now][i-1]][i-1]
            self.w[now][i] = min( self.w[now][i-1], self.w[ self.f[now][i-1] ][i-1] )
        
        for nex in self.edge[now]:
            if nex == fa :continue
            self.dfs(nex, now)
            
    def lca(self, x, y):
        x1 = self.find_father(x)
        y1 = self.find_father(y)
        if x1 != y1:
            return -1
        dx, dy = self.d[x], self.d[y]
        ans = float('inf')
        # 让x更深
        if dx < dy:
            dx, dy = dy, dx
            x, y = y, x
        # x向上跑到与y相同深度
        for i in range(19, -1, -1):
            if self.d[self.f[x][i]] >= dy:
                ans = min(ans, self.w[x][i])
                x = self.f[x][i]
        if x == y: return ans
        # x,y同时跑到lca下面两个节点
        for i in range(19, -1, -1):
            if self.f[x][i] != self.f[y][i]:
                ans = min(ans, self.w[x][i], self.w[y][i])
                x, y = self.f[x][i], self.f[y][i]
        ans = min(ans, self.w[x][0], self.w[y][0])
        return ans
    
n, m = map(int,input().split())
dic = defaultdict(dict)
v1 = []

for idx in range(m):
    x, y, z = map(int,input().split())
    v1.append([z,x,y])
v1.sort(reverse = True)

root = trie(n-1)
for w, x, y in v1:
    if root.add_path(x, y, w):
        break

# LCA
root.create()
# questions
q = int(input())
for _ in range(q):
    x, y = map(int,input().split())
    print(root.lca(x, y))