西南交通大学【机器学习实验5】

实验目的

理解神经网络原理与计算框架，包括前馈神经网络、激活函数、损失函数、后向传播过程等，学会使用梯度下降法对神经网络进行训练，学会分析不同学习率对梯度下降法收敛性影响。

实验要求

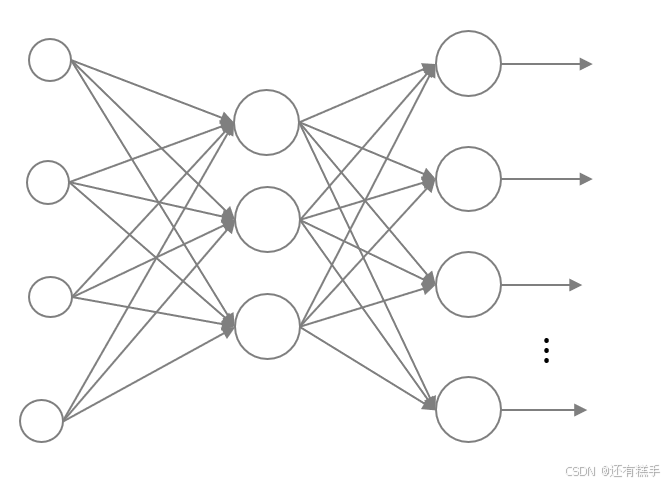
给定手写数字数据集，采用如下全连接神经网络进行分类。输入层784个节点，隐层12个节点，输出层10个节点，隐层和输出层均采用sigmoid激活函数，损失函数为均方损失函数。采用标准正态分布初始化权重和阈值参数，梯度下降最大迭代次数设置为2000，对比学习率为0.001，0.005，0.01时模型的损失函数迭代曲线和模型在测试集上的精度(accuracy)。

实验环境

Python、numpy、pandas、matplotlib

实验代码

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt

import matplotlib





matplotlib.use('TkAgg')





# 计算损失函数值

def loss(y_true, y_pred, number):

    return np.sum(np.sum((y_true - y_pred) ** 2, axis=0) / 10) / number



# 导入训练数据

train_dataset = pd.read_csv("experiment_05_training_set.csv")

train_dataset = train_dataset.values

# 得到训练数据的列和行

columnOfTrainDataset = train_dataset.shape[1]

rowOfTrainDataset = train_dataset.shape[0]

# 将y转换为独热向量方便计算损失值

yOfTrainDataset = train_dataset[:, 0]

yOneHotOfTrainDataset = np.eye(rowOfTrainDataset, 10)[yOfTrainDataset].T

# 归一化x防止在计算sigmoid函数时z过小导致结果溢出

xOfTrainDataset = train_dataset[:, 1:columnOfTrainDataset].T / 255



# 导入测试数据

test_dataset = pd.read_csv("experiment_05_testing_set.csv")

test_dataset = test_dataset.values

# 得到测试数据的行

rowOfTestDataset = test_dataset.shape[0]

# 得到测试数据的标签

yOfTestDataset = test_dataset[:, 0]

# 归一化测试数据的x

xOfTestDataset = test_dataset[:, 1:columnOfTrainDataset].T / 255



# 学习率

learn_rate = [0.001, 0.005, 0.01]

epochs = 1000



# 设置随机数种子 可以复现

np.random.seed(23)



# 标准正态分布初始化参数

W1 = np.random.randn(12, columnOfTrainDataset - 1)

B1 = np.random.randn(12, 1)



W2 = np.random.randn(10, 12)

B2 = np.random.randn(10, 1)



# 画图的x轴

x_line = np.arange(1, 1001).reshape(1000, 1)

# 循环

for learnRate in learn_rate:

    # 深拷贝参数 使每个学习率的初始化参数一致 有比较性

    w1 = W1.copy()

    b1 = B1.copy()



    w2 = W2.copy()

    b2 = B2.copy()



    # 画图的y轴

    y_line = np.zeros((1000, 1))



    # 迭代1000次

    for i in range(1, epochs+1):

        # 每次迭代开始损失值为0

        loss_value = 0



        # 计算隐藏层净输入

        hidden = w1 @ xOfTrainDataset + b1

        # 计算隐藏层输出

        hidden = 1 / (1 + np.exp(-hidden))

        # 计算输出层净输入

        output = w2 @ hidden + b2

        # 计算输出层输出

        output = 1 / (1 + np.exp(-output))

        # 计算损失值

        loss_value += loss(yOneHotOfTrainDataset, output, rowOfTrainDataset)

        # 计算输出层的误差

        e2 = 0.08 * (output - yOneHotOfTrainDataset) * output * (1 - output)



        # 计算输出层权重矩阵的梯度

        w2_grad = e2 @ hidden.T

        # 计算输出层偏置的梯度

        b2_grad = np.sum(e2, axis=1).reshape(-1, 1)

        # 反向计算隐藏层误差

        e1 = hidden * (1 - hidden) * (w2.T @ e2)

        # 计算隐藏层权重矩阵的梯度

        w1_grad = e1 @ xOfTrainDataset.T

        # 计算隐藏层偏置的梯度

        b1_grad = np.sum(e1, axis=1).reshape(-1, 1)



        # 更新画图的y轴

        y_line[i-1, 0] = loss_value



        # 更新参数

        w1 -= learnRate * w1_grad

        b1 -= learnRate * b1_grad

        w2 -= learnRate * w2_grad

        b2 -= learnRate * b2_grad



        # 打印过程信息

        if i % 200 == 0 or i == 1:

            print(f"epoch: {i}, loss: {y_line[i-1, 0]: .6f}")



    # 开始计算精度

    hidden = w1 @ xOfTestDataset + b1

    hidden = 1 / (1 + np.exp(-hidden))

    output = w2 @ hidden + b2

    output = 1 / (1 + np.exp(-output))

    A = np.sum(np.argmax(output, axis=0).T == yOfTestDataset)



    # 打印精度信息

    print(f"learning rate: {learnRate}, Accuracy: {A/rowOfTestDataset: .6f}")

    print("--------------------------------------------------------------")



    # 调整参数生成图像

    plt.plot(x_line, y_line, color='b', linewidth=1.5, label='Loss function')

    plt.ylim(0, 0.5)

    plt.title(f"learning rate: {learnRate} Loss function", fontsize=14)

    plt.xlabel("Epoch", fontsize=12)

    plt.ylabel("Loss function value", fontsize=12)

    plt.legend(loc='upper right', frameon=True)

    plt.grid(alpha=0.3, linestyle=':')

    plt.tight_layout()

    plt.show()

结果分析

学习率为0.001时损失迭代曲线：

学习率为0.005时损失迭代曲线：

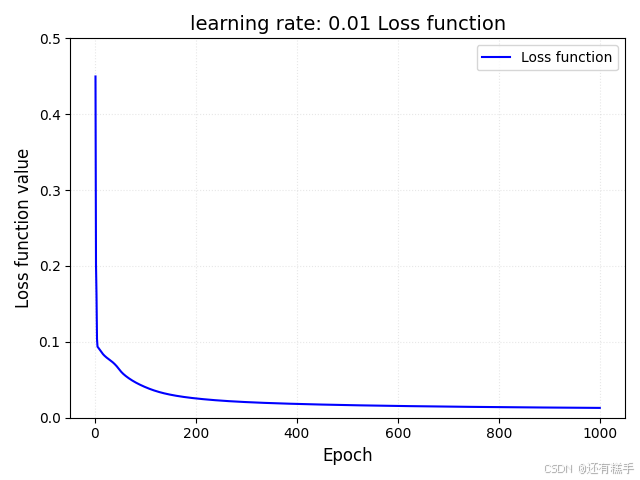
学习率为0.01时损失迭代曲线：

学习率	0.001	0.005	0.01
精度	0.775250	0.885083	0.904583