深度学习入门笔记手稿(二)偏差与方差
偏差与方差
通过判断网络系统中训练集误差和验证集误差来判断情况:
图中给出了两种划分方式,线为决策边界。一种欠拟合 高偏差,一种过拟合高方差两种情况。
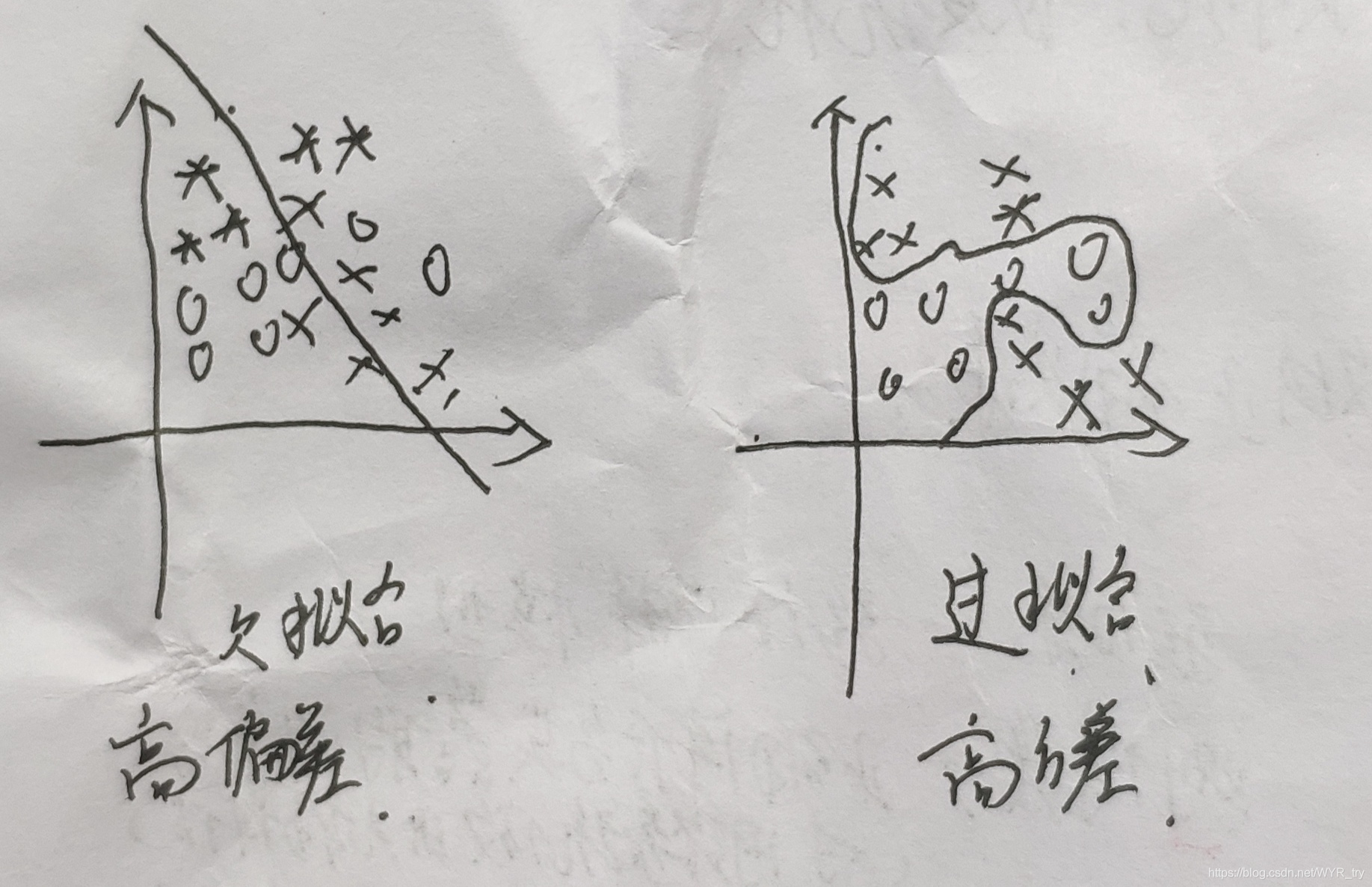
如何判断是高偏差还是高方差,下面给出在一个分类网络系统中出现的4种情况
A:训练集误差 1%,验证集误差11%
B:训练集误差 15%,验证集误差16%
C:训练集误差 15%,验证集误差30%
D:训练集误差 0.5%,验证集误差1%
A中:训练集设置较好,验证集相对较差,可能过度拟合训练集,高方差
B中:训练集误差和验证集误差都比较大且接近,高偏差
C中:训练集误差和验证集误差都比较大但是验证集误差大的太多。高方差 高偏差
D中:这种情况就是低偏差 低方差
通过判断偏差 和方差来选择不同的方法优化算法
训练神经网络的基本方法:初始模型训练完成后,首先看算法偏差情况,若偏差较高,则试着评估训练集性能,若偏差特别高(无法拟合训练集),则选择一个新网络(含有更多隐藏层或单元)或花费更多时间训练网络或尝试其他算法。
采用规模更大的网络通常有帮助,延时不一定,只要扩大网络规模,人眼能分辨图片,则网络至少能拟合训练集
一旦偏差降到可接受范围,再研究方差,评估方差,先查看验证集性能,若方差高最好的解决办法是采用更多的数据,当无法获得更多的数据也可采用正则化。
一个合适的神经网络能同时减少偏差和方差
只要正则适度通常构建一个更大的网络便可不影响方差的同时减少偏差而采用更多的数据通常可以不影响偏差的同时减小方差
最后一点 训练一个大型神经网路的主要代价只是计算时间(网络比较规范)







 本文探讨了深度学习中偏差与方差的概念,分析了四种不同情况下训练集与验证集的误差表现,介绍了如何通过判断偏差和方差来选择优化算法,包括增加网络复杂度、调整正则化参数和增加训练数据等策略。
本文探讨了深度学习中偏差与方差的概念,分析了四种不同情况下训练集与验证集的误差表现,介绍了如何通过判断偏差和方差来选择优化算法,包括增加网络复杂度、调整正则化参数和增加训练数据等策略。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








