【初识C09】青蛙跳台阶 | 汉诺塔

青蛙跳台阶

等于斐波那契数：

int Fibna(int x)
{
	if(x==0)
	return 0；
	if(x<2)
	{
		return 1;
	}
	else
	{
		return Fibna(x-2)+Fibna(x-1);
	}
}
 int main()
 {
 	int fib=0;
 	printf("你想要第几个台阶的跳法：");
 	scanf("%d",&fib);
 	int ret = Fibna(fib);	
 }

汉诺塔

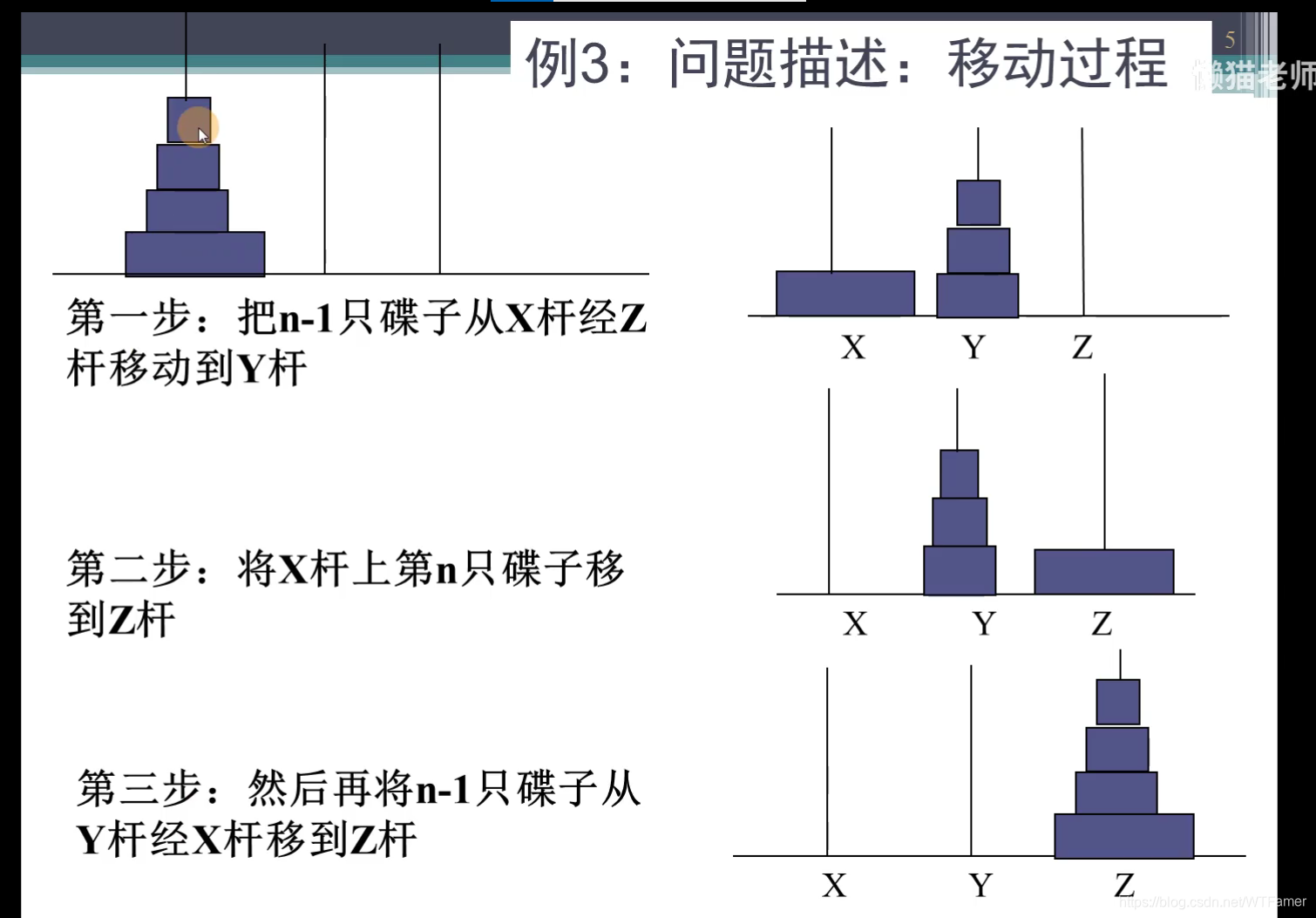
1. 汉诺塔问题的描述

• 汉诺塔（Tower of Hanoi）是一个经典的数学问题和递归算法的演示实例。它由三根柱子（通常标记为 A、B、C）和若干大小不同的圆盘组成，初始时所有圆盘按照从大到小的顺序堆叠在一根柱子（比如 A 柱）上。
• 目标是将所有圆盘从起始柱子（A 柱）移动到目标柱子（比如 C 柱），在移动过程中需要遵循以下规则：
  • 每次只能移动一个圆盘。
  • 大盘不能放在小盘上面。

2. 递归算法解决汉诺塔问题的思路

• 对于汉诺塔问题，可以将其分解为子问题来解决，递归是一种非常自然的解决方式。
• 基本的递归思路如下：
  • 将除最底层圆盘外的所有圆盘从起始柱子（A）移动到中间柱子（B），这是一个规模较小的汉诺塔问题。
  • 将最底层圆盘从起始柱子（A）移动到目标柱子（C）。
  • 最后将中间柱子（B）上的圆盘移动到目标柱子（C），这又是一个规模较小的汉诺塔问题。

3. C 语言实现汉诺塔的代码示例

#include <stdio.h>

// 定义函数用于移动圆盘
void move(int disk, char source, char destination) {
    printf("Move disk %d from %c to %c\n", disk, source, destination);
}

// 汉诺塔递归函数
void towerOfHanoi(int n, char source, char auxiliary, char destination) {
    if (n == 1) {
        move(1, source, destination);
    } else {
        // 将 n - 1 个圆盘从 source 移动到 auxiliary
        towerOfHanoi(n - 1, source, destination, auxiliary);
        // 将最大的圆盘从 source 移动到 destination
        move(n, source, destination);
        // 将 n - 1 个圆盘从 auxiliary 移动到 destination
        towerOfHanoi(n - 1, auxiliary, source, destination);
    }
}

int main() {
    int numDisks;
    printf("Enter the number of disks: ");
    scanf("%d", &numDisks);
    towerOfHanoi(numDisks, 'A', 'B', 'C');
    return 0;
}

• 在上述代码中，move函数用于输出移动圆盘的操作信息。towerOfHanoi函数是递归函数，它接受圆盘数量n以及三根柱子的标记作为参数。当n等于 1 时，直接将圆盘从起始柱子移动到目标柱子；当n大于 1 时，通过递归调用将问题分解为三个步骤来解决。

4. 时间复杂度和空间复杂度分析

• 时间复杂度：对于有n个圆盘的汉诺塔问题，其时间复杂度为$O(2^n)$。因为每次递归调用都会将问题规模减半，但同时会产生两个新的递归调用，导致计算次数呈指数增长。
• 空间复杂度：空间复杂度主要取决于递归调用栈的深度，由于每次递归调用时n减 1，直到n等于 1 为止，所以递归调用栈的深度为n，因此空间复杂度为$O(n)$。

void move(char x, char z)
{
	printf("%c->%c\n", x, z);
}
void Hanoi(int n, char x, char y, char z)
{
	if (n == 1)
	{
		move(x, z);
	}
	else
	{
		Hanoi(n - 1, x, z, y);
		move(x, z);
		Hanoi(n - 1, y, x, z);
	}
}

int main()
{
	int n = 0;
	scanf("%d", &n);
	Hanoi(n, 'a', 'b', 'c');
}