PyTorch深度学习神经网络实战：PyTorch神经网络基础-层与神经元-优快云博客

1.2.1 生物神经元

生物神经元是生物体神经系统的基本单位。它们通过一系列步骤工作：

信号接收：“树突”，神经元的分支延伸，接收来自其他神经元或感觉感受器的信号。
信号整合：接收到的信号在神经元的细胞体中进行整合。这个积分过程涉及输入信号的求和。
信号传导：如果积分信号超过一定阈值，就会产生称为动作电位的电脉冲。这种动作电位沿着“轴突”（一种长纤维样结构）向“突触”行进。
信号传播：在“突触”处，电脉冲被转换成化学信号。神经递质被释放到突触中，使信号被传递到下一个神经元的树突。
信号处理：该过程在随后的“神经元”中重复，使信号在整个神经系统中传播。

1.2.2 人工神经元

人工神经元，也称为节点或感知器，是一种旨在模仿生物神经元行为的数学模型。它们以不同的方式运行：

信号接收：人工神经元接收来自前一层或外部源的输入信号，通常表示为数值。
信号加权：每个输入信号都乘以相应的weight。这些权重决定了每个输入对整体计算的重要性或贡献。
信号求和：加权后的输入信号求和，通常使用线性组合。
激活函数：求和的信号通过激活函数传递，该函数将非线性引入计算中。激活函数根据输入信号确定人工神经元的输出。
信号传输：然后将人工神经元的输出传输到下一层或作为神经网络的最终输出。
反向传播：神经网络中的神经通过调整与其连接相关的权重和偏差来学习。这个过程被称为“反向传播”，允许网络优化其性能并做出准确的预测。

1.3 神经元的基本组成

人工神经网络中的神经元与它们的生物学对应的神经元相似，并具有三个主要组成部分：

输入：神经元接收来自前一层或外部源的输入信号。这些输入乘以相应的权重，然后求和。
激活函数：通过激活函数传递输入的加权和，激活函数将非线性引入网络。激活函数根据输入信号确定神经元的输出。
输出：神经元的输出是应用于输入的加权和的激活函数的结果。然后，这个输出被传输到下一层神经元。

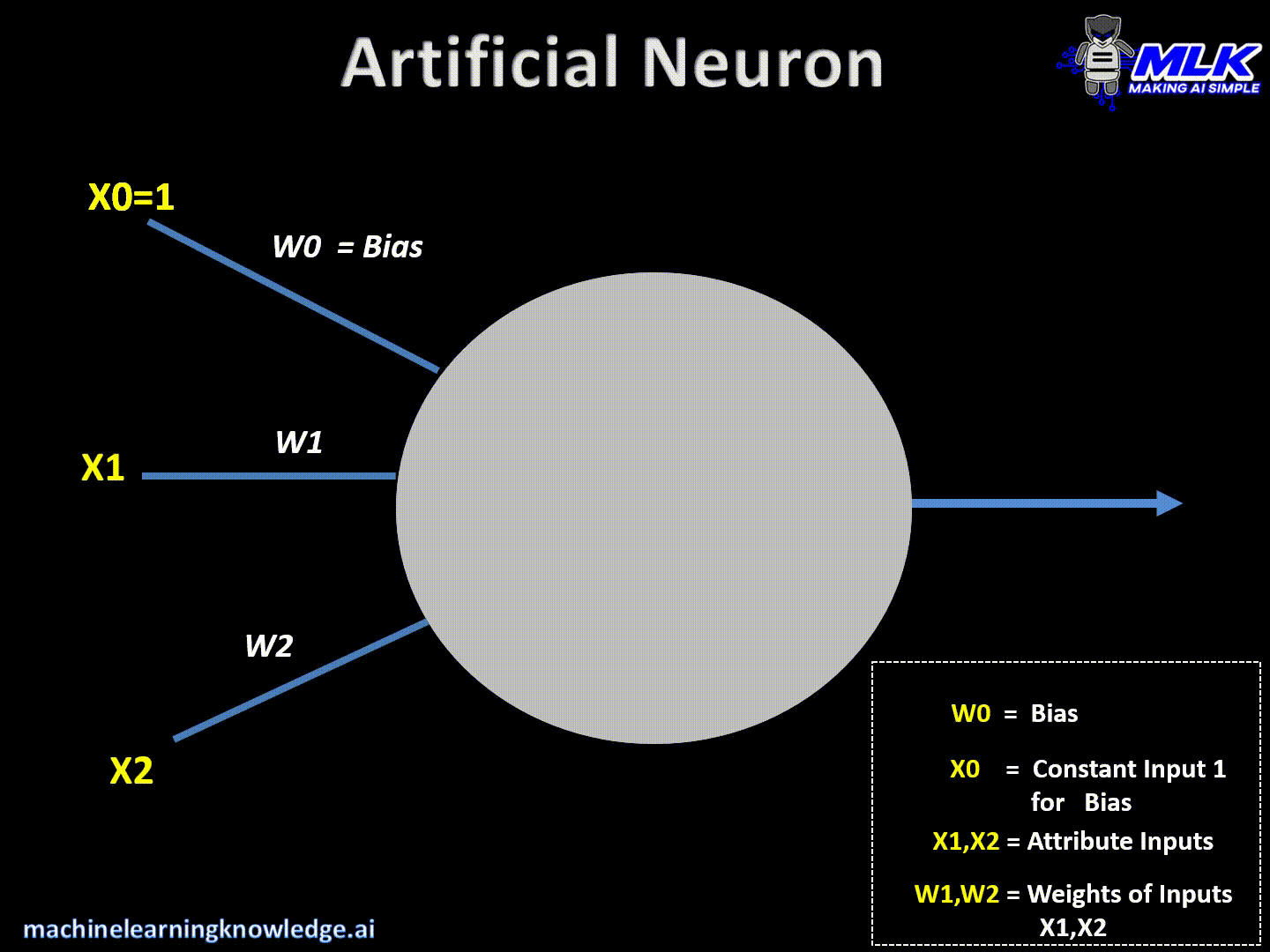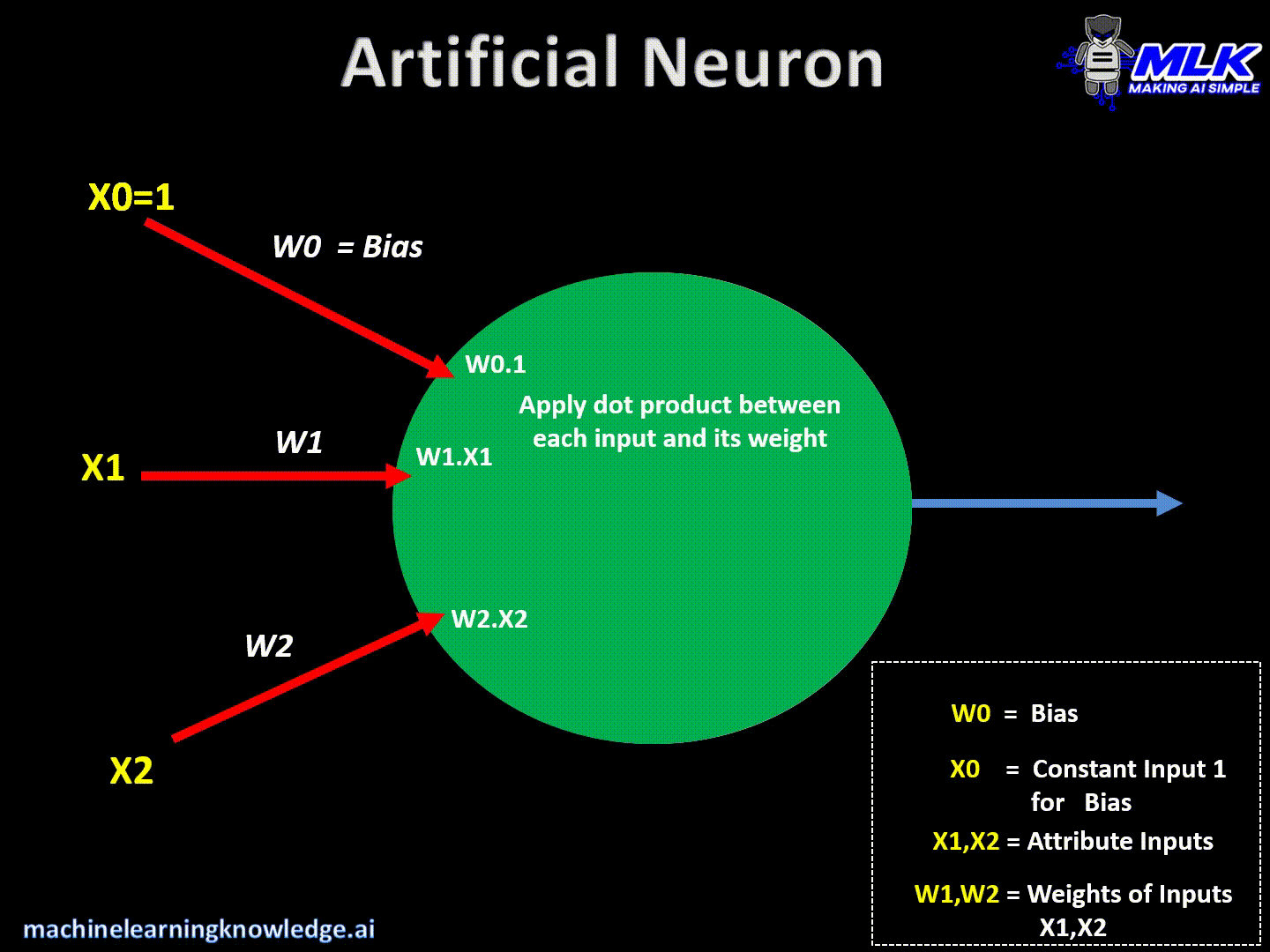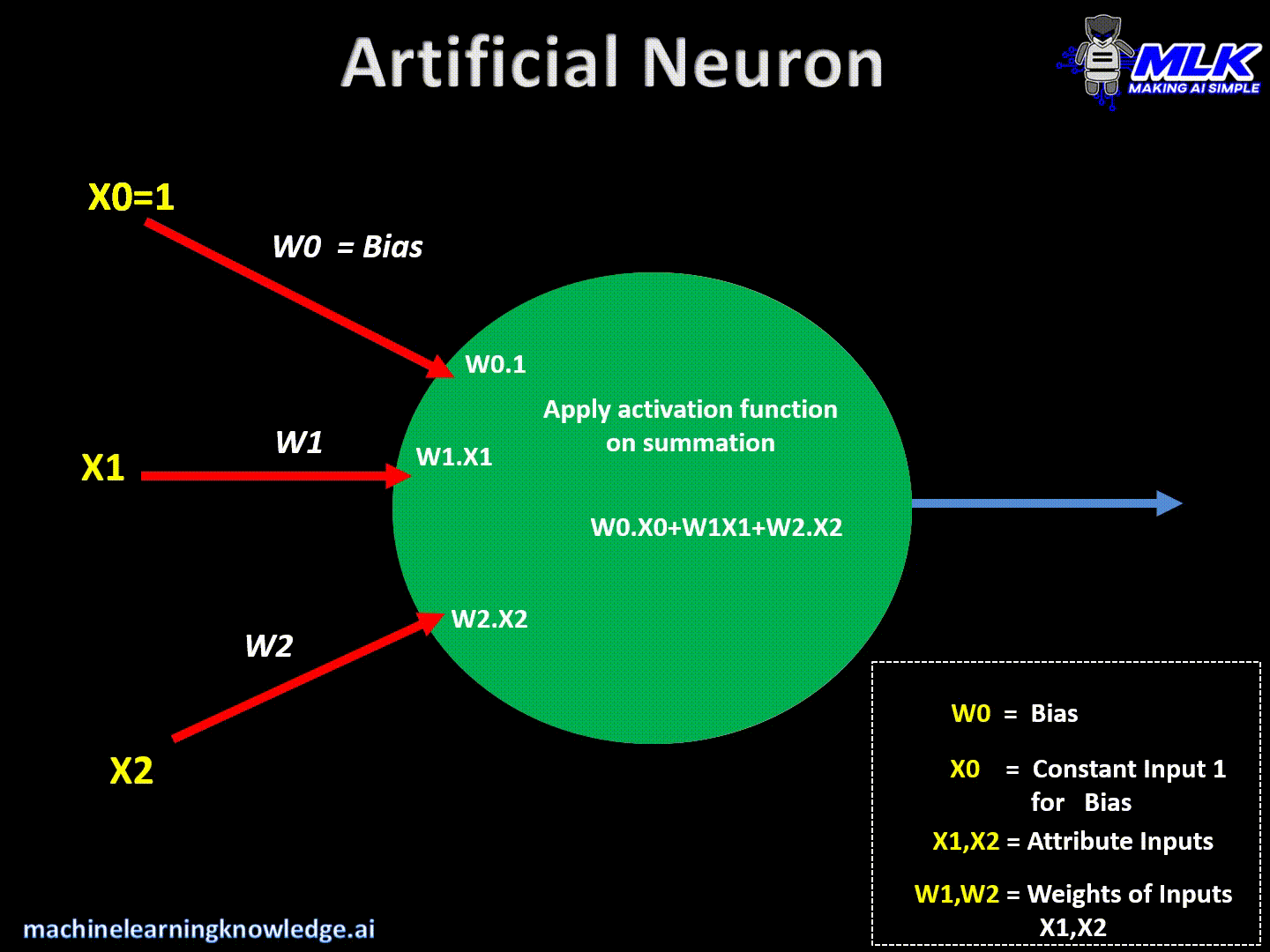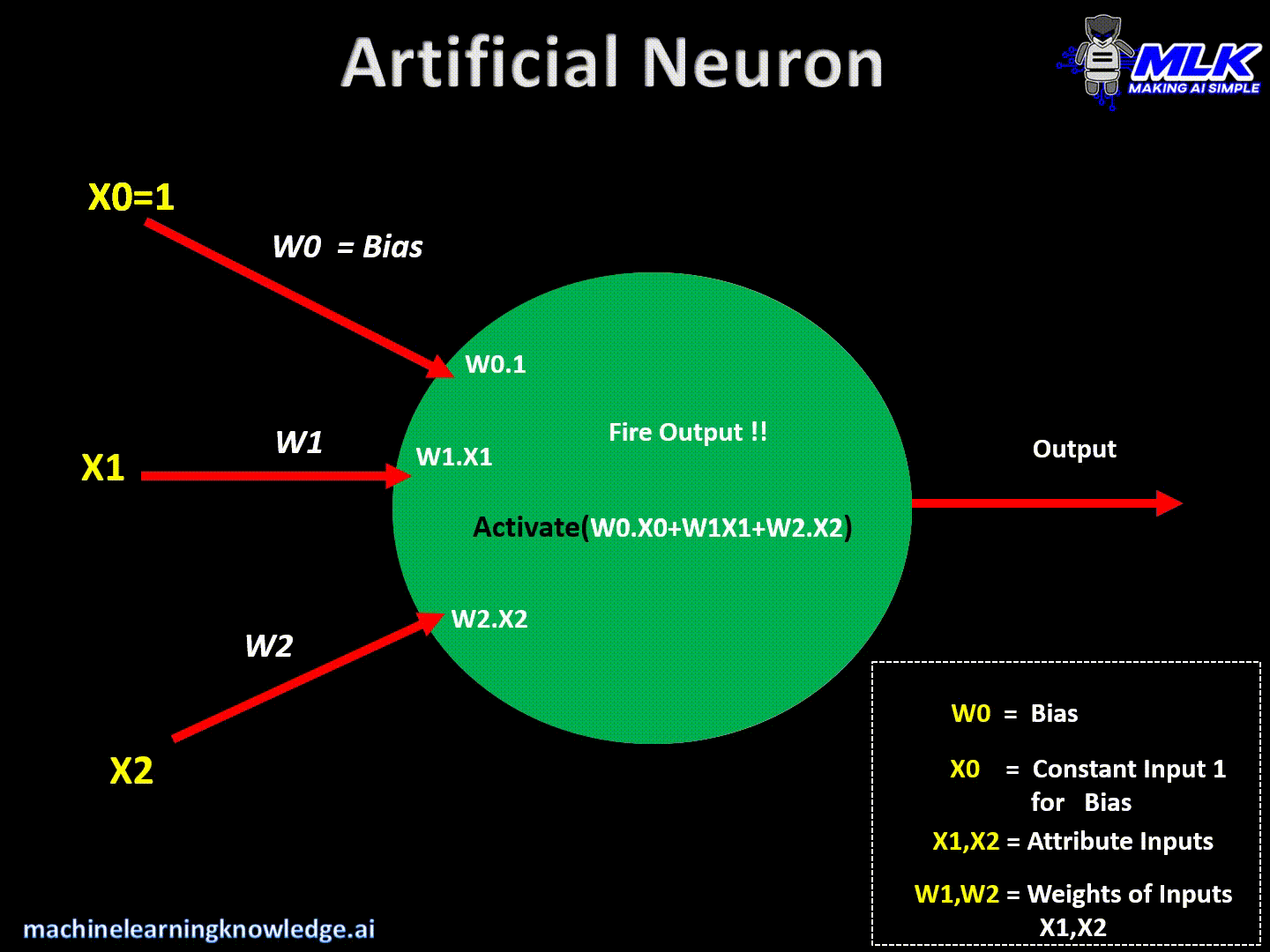
图3：实验设备

1.3.1 神经元权重和偏置

在人工神经网络（ANN）中，每个神经元接收来自前一层或外部源的输入信号。将这些输入信号乘以相应的权重，然后求和。此外，在通过激活函数之前，将偏置项添加到加权和中。
神经元的数学公式可以表示为：

$\sum_{i=1}^{n} (w_i \cdot x_i) + b$

$out=activation_function(z) out = \text{activation\_function}(z)$

$z$ 是输入加上偏置项的加权和，
$w_i$ 表示分配给每个输入 $x_i$ 的权重，
$b$ 是偏倚项，
$o u t$ 是神经元经过激活函数后的输出。

它们是什么

权重：分配给每个输入 $x_i$ 信号的权重 $w_i$ 决定了该输入对神经元整体计算的重要性或贡献。权重越大，表示相应的输入对神经元输出的影响越强。通过在训练期间调整权重，网络学会将“更高的权重分配给更重要的特征，将更低的权重分配给不重要的特征”。
偏置：偏置项 $b$ 允许神经元独立于输入信号调整其输出。它作为偏移量或“阈值”，决定神经元的激活水平。正偏置会将激活函数右移，而负偏置会将其左移.通过调整偏置，网络可以控制神经元的整体输出。

理解并适当地设置神经元的权重和偏置对于人工神经网络的性能和有效性至关重要。在训练过程中不正确的初始化或不正确的调整会导致次优结果，甚至出现收敛问题。

如何计算它们

计算神经元权重和偏置的过程包括两个主要步骤：

初始化：初始时，神经元的权重 $w_i$ 和偏置 $b$ 被随机分配或用较小的值初始化。这种随机初始化有助于打破对称性，并允许网络学习不同的特征。
训练：在训练过程中，网络调整权重 $w_i$ 和偏置 $b$ ，以最小化预测输出和实际输出之间的差异。这种调整是使用优化算法完成的，例如梯度下降，它根据预测和实际输出之间的误差迭代更新权重 $w_i$ 和偏置 $b$ 。

1.3.2 激活函数

神经元的激活函数根据输入的加权和确定其输出。它将非线性引入神经网络，使其能够学习复杂的模式并做出预测。

常用的激活函数包括：


Step	Sigmoid	Tanh

ReLU	LReLU	Softmax

import numpy as np

步进激活函数

基于阈值输出二进制值的简单激活函数。如果输入小于阈值，则返回0，否则返回1。阶跃函数经常用于二元分类问题。

数学函数可以表示为：

$\text{step}(x) = \begin{cases} 1, & \text{{if }} x \geq 0 \\ 0, & \text{{otherwise}} \end{cases}$

def step(x):

    return np.where(x >= 0, 1, 0)

Sigmoid激活函数

常用于二分类问题的输出层。它将输出压缩在0和1之间，表示正类的概率。如果在隐藏层中使用，可能会导致消失梯度问题。

sigmoid数学函数可以表示为：

$\text{sigmoid}(x) = \frac{1}{{1 + e^{-x}}}$

def sigmoid(x):

    return 1 / (1 + np.exp(-x))

Tanh（双曲切线）激活函数

压缩-1和1之间的输入值。它围绕原点对称，对于捕获数据中的非线性关系非常有用。如果在隐藏层中使用，可能会导致消失梯度问题。

双曲正切（tanh）函数的数学表示是：

$\text{tanh}(x) = \frac{{e^x - e^{-x}}}{{e^x + e^{-x}}}$

def tanh(x):

    return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))

ReLU（整流线性单元）激活函数

将所有负值设置为零，并保持正值不变。会患上垂死的神经元问题“垂死的ReLU”。

ReLU（整流线性单元）激活函数的数学表示是：

$\text{ReLU}(x) = \max(0, x)$

def relu(x):
    
    return np.maximum(0, x)

LReLU（泄漏ReLU）激活函数

ReLU激活函数的变体，允许小的负值，而不是将其设置为零。这有助于缓解“死亡ReLU”问题，即神经元可能变得不活跃并停止学习。

Leaky ReLU (LReLU)的数学表示是：

$\text{LReLU}(x) = \begin{cases} x, & \text{if } x \geq 0 \\ \alpha x, & \text{otherwise} \end{cases}$

其中 $α\alpha$ 是一个小的正常数，用于确定负值 $x$ 时函数的斜率。

def lrelu(x, alpha=0.01):

    return np.where(x >= 0, x, alpha * x)

Softmax激活函数

常用于多类分类问题的输出层。它将输出归一化为类上的概率分布。

softmax激活函数的数学表示为：

$\text{softmax}(x_i) = \frac{{e^{x_i}}}{{\sum_{j=1}^{n} e^{x_j}}}$

其中 $x_i$ 表示 $i$ 元素的输入值， $n$ 是输入向量中元素的总数。

def softmax(x):

    exps = np.exp(x - np.max(x, axis=1, keepdims=True))
    return exps / np.sum(exps, axis=1, keepdims=True)

附录：softMax激活函数计算过程详解

Softmax激活函数常用于多分类问题的输出层，它能将一组任意实数（通常是模型的原始输出，称为“logits”）转换为范围在[0, 1]且总和为1的概率分布，直观表示每个类别的预测概率。

Softmax计算公式

对于输入向量x = [x₁, x₂, ..., xₙ]，Softmax的计算如下：
$\text{Softmax}(x_i) = \frac{e^{x_i}}{\sum_{j=1}^{n} e^{x_j}}$
其中：

分子是输入元素x_i的指数函数（e为自然常数，约2.718）；
分母是所有输入元素的指数函数之和，确保输出总和为1。

具体例子：三分类问题

假设模型对一个样本的原始输出（logits）为：
logits = [2.0, 1.0, 0.1]

我们用Softmax将其转换为概率分布，步骤如下：

步骤1：计算每个元素的指数（分子）

$\begin{align*} e^{2.0} &\approx 7.389 \\ e^{1.0} &\approx 2.718 \\ e^{0.1} &\approx 1.105 \\ \end{align*}$

步骤2：计算指数之和（分母）

$\sum e^{x_j} = 7.389 + 2.718 + 1.105 \approx 11.212$

步骤3：每个元素的指数除以总和，得到概率

$KaTeX parse error: Unexpected end of input in a macro argument, expected '}' at end of input: …\ \end{align*}$

结果验证

概率总和：0.659 + 0.242 + 0.099 = 1.0，符合Softmax的特性。

在这个例子中，模型预测该样本属于第一个类别的概率最高（65.9%）。

PyTorch代码验证

用PyTorch的torch.softmax函数可以快速实现上述计算：

import torch

logits = torch.tensor([2.0, 1.0, 0.1])
probabilities = torch.softmax(logits, dim=0)  # dim=0表示对第0维（向量本身）计算

print(probabilities)  # 输出：tensor([0.6590, 0.2424, 0.0986])
print(probabilities.sum())  # 输出：tensor(1.0000)（总和为1）