SciPy科学计算与应用：SciPy插值技术入门-线性与样条插值

最新推荐文章于 2025-09-28 01:47:38 发布

原创最新推荐文章于 2025-09-28 01:47:38 发布 · 843 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#scipy

插值方法：从理论到实践

学习目标

通过本课程，学员将深入了解SciPy库中的插值模块scipy.interpolate，并且通过理论与实践相结合的方式，掌握线性插值和样条插值的基本原理及其在Python中的实现方法。学员将能够根据实际需求选择合适的插值方法，并应用于数据处理和分析中。

学习内容

1 插值方法：从理论到实践

1.1 线性插值

线性插值是一种简单且常用的插值方法，它通过连接两个已知数据点之间的直线来估计这两点之间的值。这种方法假设在这两点之间，数据的变化是线性的。线性插值在数据点稀疏或数据变化平缓的情况下非常有效，但在数据变化剧烈或数据点密集的情况下，可能会导致较大的误差。

1.1.1 线性插值的数学原理

假设我们有两个已知的数据点$ (x_1, y_1)$ 和 $x_2, y_2)$ ，其中 $x_1 < x_2$ 。对于任意一个 $x$ ，其中 $x1≤x≤x2x_1 \leq x \leq x_2$ ，线性插值的公式为：
$y_1 + \frac{(y_2 - y_1)}{(x_2 - x_1)}(x - x_1)$
这个公式表示$ y $是 $x $的线性函数，通过这条直线可以估计$ x_1$ 和 $x_2$ 之间的任何 $x$ 值对应的 $y$ 值。

1.1.2 Python实现

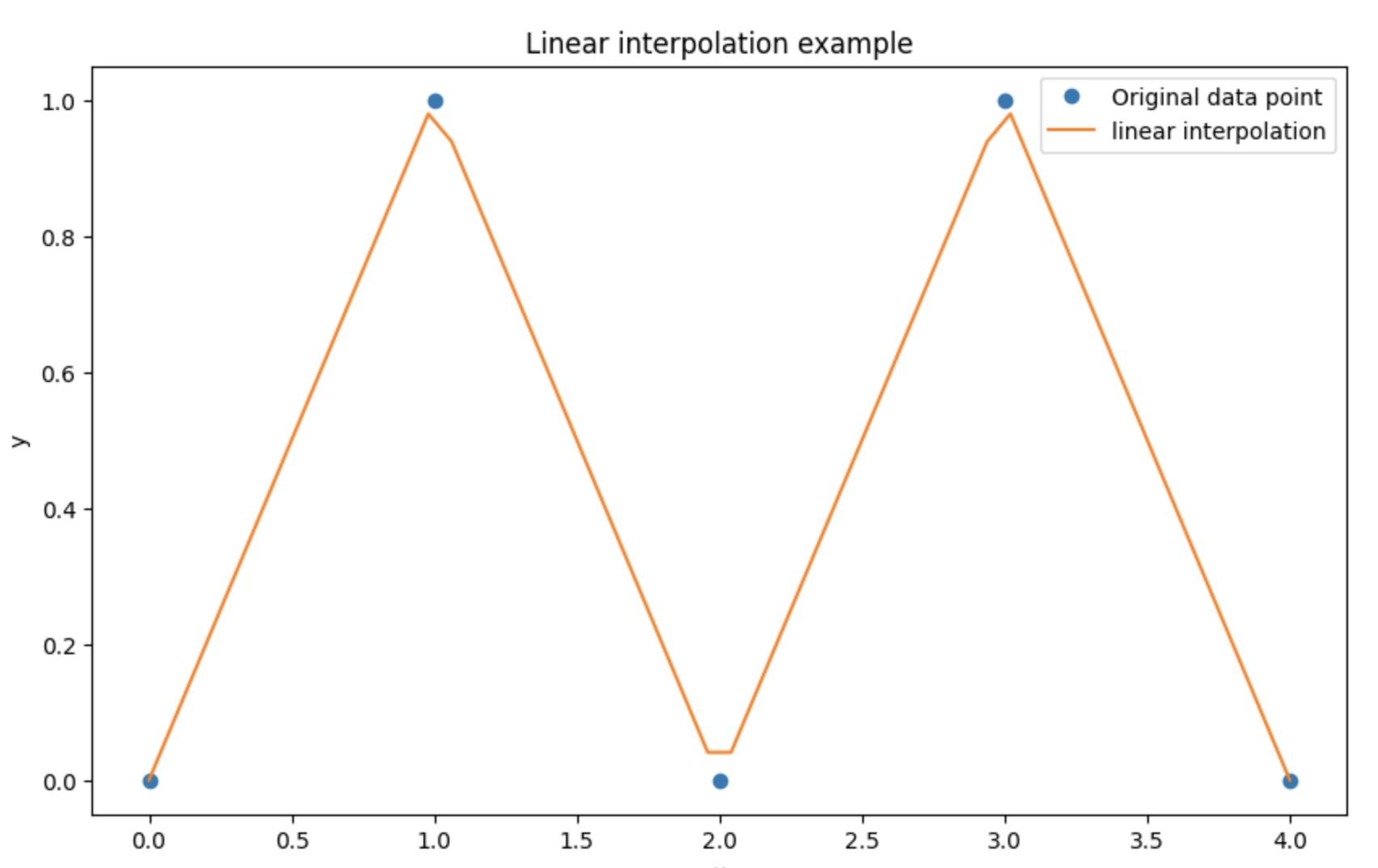
在Python中，我们可以使用scipy.interpolate模块中的interp1d函数来实现线性插值。下面是一个简单的示例：

import numpy as np
from scipy.interpolate import interp1d
import matplotlib.pyplot as plt

# 已知数据点
x = np.array([0, 1, 2, 3, 4])
y = np.array([0, 1, 0, 1, 0])

# 创建线性插值函数
linear_interpolation = interp1d(x, y, kind='linear')

# 生成新的x值
x_new = np.linspace(0, 4, 50)

# 计算新的y值
y_new = linear_interpolation(x_new)

# 绘制图形
plt.figure(figsize=(10, 6))
plt.plot(x, y, 'o', label='Original data point')
plt.plot(x_new, y_new, '-', label='linear interpolation')
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
plt.title('Linear interpolation example')
plt.show()

在这里插入图片描述

1.2 样条插值

样条插值是一种更高级的插值方法，它通过在数据点之间拟合多项式曲线来估计值。样条插值可以分为多种类型，如线性样条、二次样条和三次样条等。其中，三次样条插值最为常用，因为它在保证平滑性的同时，还能较好地拟合数据点。

1.2.1 三次样条插值的数学原理

三次样条插值通过在每个相邻的数据点之间拟合一个三次多项式，使得这些多项式在数据点处的值、一阶导数和二阶导数都相等。这样可以确保插值曲线在数据点处平滑过渡，避免了线性插值可能出现的尖锐转折。

1.2.2 Python实现

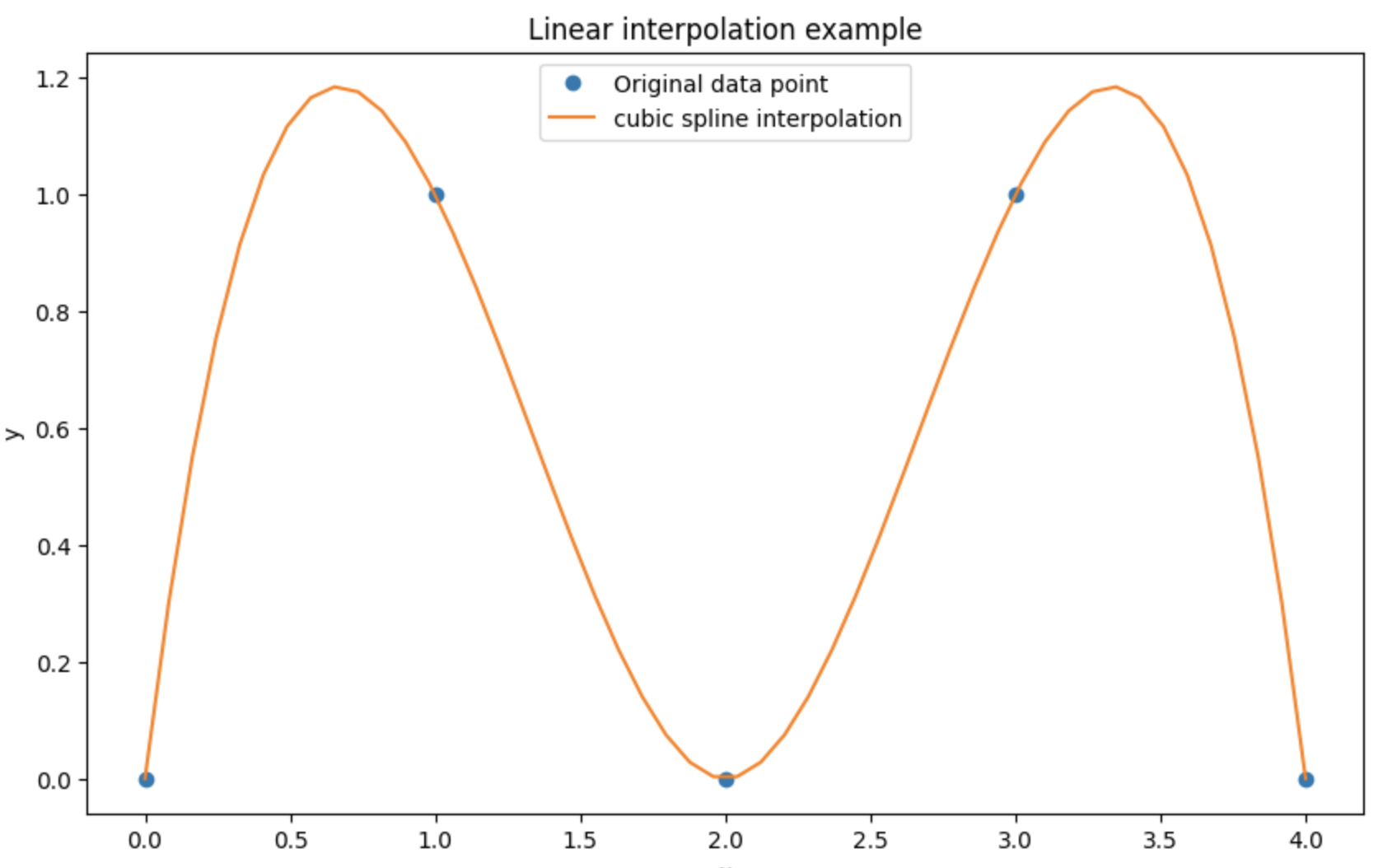
在Python中，我们可以使用scipy.interpolate模块中的interp1d函数来实现三次样条插值。下面是一个简单的示例：

import numpy as np
from scipy.interpolate import interp1d
import matplotlib.pyplot as plt

# 已知数据点
x = np.array([0, 1, 2, 3, 4])
y = np.array([0, 1, 0, 1, 0])

# 创建三次样条插值函数
cubic_spline_interpolation = interp1d(x, y, kind='cubic')

# 生成新的x值
x_new = np.linspace(0, 4, 50)

# 计算新的y值
y_new = cubic_spline_interpolation(x_new)

# 绘制图形
plt.figure(figsize=(10, 6))
plt.plot(x, y, 'o', label='Original data point')
plt.plot(x_new, y_new, '-', label='cubic spline interpolation')
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
plt.title('Linear interpolation example')
plt.show()

在这里插入图片描述

1.3 SciPy插值模块的使用

scipy.interpolate模块提供了多种插值方法，除了线性插值和样条插值外，还包括最近邻插值、零阶保持插值等。这些方法在不同的应用场景中各有优势，选择合适的插值方法对于数据处理和分析至关重要。

1.3.1 插值方法的选择

选择合适的插值方法需要考虑以下几个因素：

数据的特性：数据是否平滑、是否有突变等。
插值的精度：需要多高的插值精度。
计算的复杂度：插值方法的计算复杂度和运行时间。

1.3.2 实践示例

假设我们有一组实验数据，需要通过插值方法来估计数据点之间的值。我们将使用线性插值和三次样条插值进行比较，观察不同插值方法的效果。

import numpy as np
from scipy.interpolate import interp1d
import matplotlib.pyplot as plt

# 实验数据
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([0, 0.8, 0.9, 0.1, -0.8, -1.0])

# 创建线性插值函数
linear_interpolation = interp1d(x, y, kind='linear')

# 创建三次样条插值函数
cubic_spline_interpolation = interp1d(x, y, kind='cubic')

# 生成新的x值
x_new = np.linspace(0, 5, 100)

# 计算新的y值
y_linear = linear_interpolation(x_new)
y_cubic = cubic_spline_interpolation(x_new)

# 绘制图形
plt.figure(figsize=(10, 6))
plt.plot(x, y, 'o', label='Original data point')
plt.plot(x_new, y_linear, '-', label='linear interpolation')
plt.plot(x_new, y_cubic, '--', label='cubic spline interpolation')
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
plt.title('Comparison Between Linear Interpolation and Cubic Spline Interpolation')
plt.show()

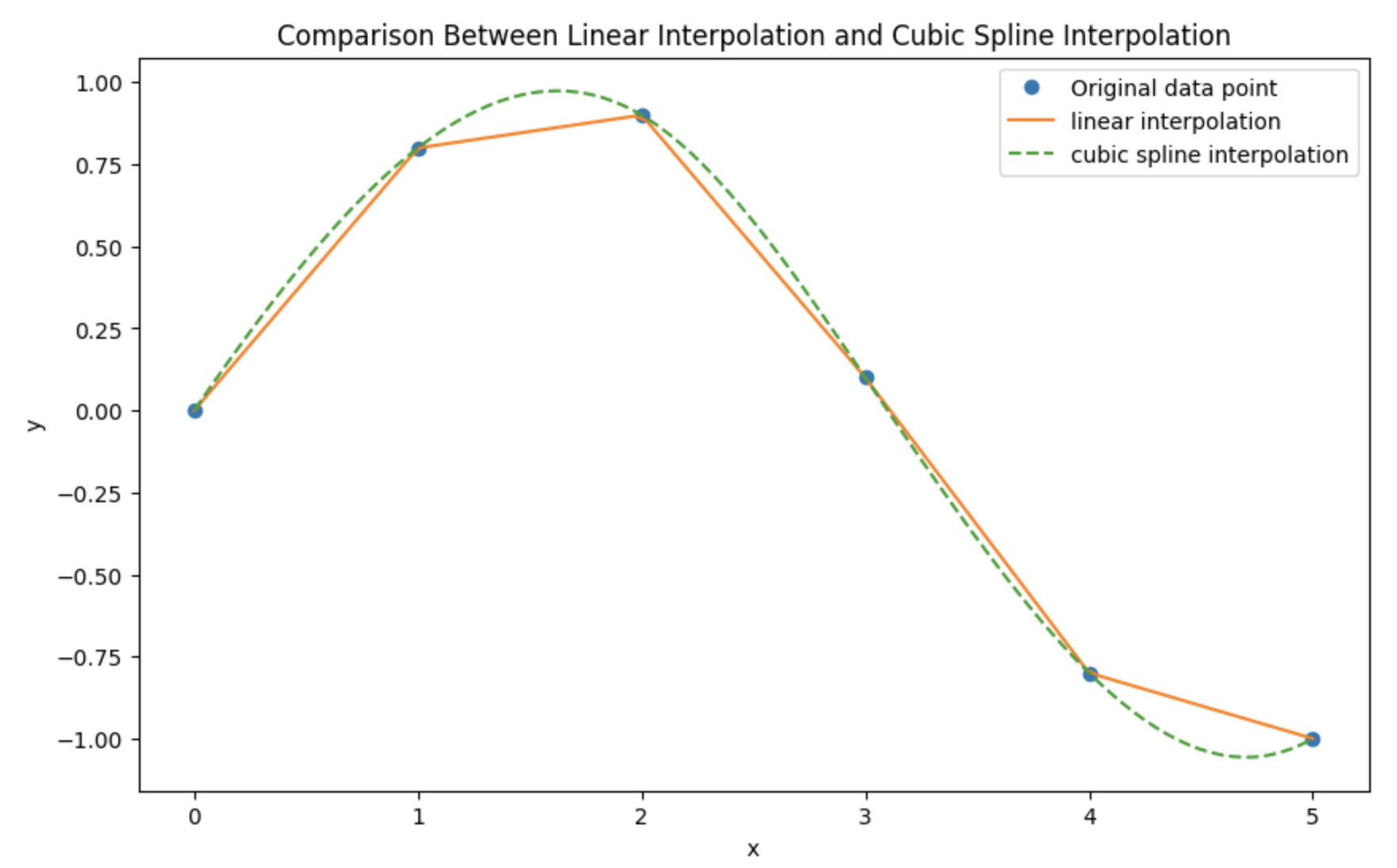
在这里插入图片描述
通过上述示例，我们可以看到线性插值和三次样条插值在处理同一组数据时的不同效果。线性插值简单直接，但可能会导致数据点之间的变化不够平滑；而三次样条插值虽然计算复杂度较高，但能够更好地拟合数据点，提供更平滑的插值结果。
最终本课程通过理论与实践相结合的方式，详细介绍了SciPy库中的插值模块scipy.interpolate，重点讲解了线性插值和样条插值的基本原理及其在Python中的实现方法。学员通过本课程的学习，将能够根据实际需求选择合适的插值方法，并应用于数据处理和分析中。