ybt1941 Hanoi双塔问题（NOIP2007普及组第4题）（高×低）

ybt1941  Hanoi双塔问题（NOIP2007普及组第4题）

时空限制    1000ms/64MB

题目描述

        给定A、B、C三根足够长的细柱，在A柱上放有2n个中间有孔的圆盘，共有n个不同的尺寸，每个尺寸都有两个相同的圆盘，注意这两个圆盘是不加区分的（下图为n=3的情形）。

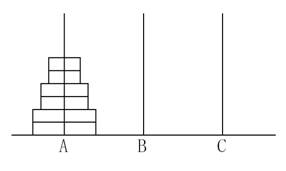
        现要将这些圆盘移到C柱上，在移动过程中可放在B柱上暂存。要求：

        （1）每次只能移动一个圆盘；

        （2）A、B、C三根细柱上的圆盘都要保持上小下大的顺序；

        任务：设An为2n个圆盘完成上述任务所需的最少移动次数，对于输入的n，输出An。

输入

        输入文件hanoi.in为一个正整数n，表示在A柱上放有2n个圆盘。

输出

        输出文件hanoi.out仅一行，包含一个正整数, 为完成上述任务所需的最少移动次数An。

输入样例1

1

输出样例1

2

输入样例2

2

输出样例2

6

说明

【限制】

        对于50%的数据，1<=n<=25

        对于100%的数据，1<=n<=200

【提示】

        设法建立An与An-1的递推关系式。

分析

        汉诺塔移动n个盘的次数是2^n -1次，比如移动一个盘1次，两个盘3次，三个盘7次......

那么汉诺双塔移动2n个盘的次数：看成移动n组盘（每组2个相同的）移动组数就是2^n -1次，每组每次移动2次。答案：2*(2^n -1)次   即 2^(n+1) -2。就是求高精度数  2^(n+1) -2

代码

法一：数组模拟

#include<iostream>
#include<cstring>
using namespace std;
const int N = 100;
int n,a[N];

void pow(int n,int a[]){
	memset(a,0,sizeof(int)*N);
	a[0] = a[1] = 1;
	for (int i=1; i<=n; ++i){
		for (int j=1; j<=a[0]; ++j) a[j]*=2;
		for (int j=1; j<=a[0]; ++j)
			a[j+1]+=a[j]/10,a[j]%=10;
		if (a[a[0]+1]) a[0]++;
	}
}

void output(int a[]){
	for (int i=a[0]; i>1; --i) cout<<a[i];
	cout<<a[1]-2<<'\n';	//单独处理-2问题
}

int main(){
	cin>>n;
	pow(n+1,a);
	output(a);
	return 0;
}

法二：重载运算符

#include<iostream>
#include<cstring>
using namespace std;
const int N = 100;
struct bign{
	int len,d[N];
	bign(){ memset(d,0,sizeof(d)); len=1; }	//构造函数，默认初始化
	bign(int x){							//构造函数，int初始化
		memset(d,0,sizeof(d));
		len = 0;
		do {
			d[++len] = x%10;
			x /= 10;
		} while (x);
	}
	bign operator * (const int &b){		//重载* 高*低
		bign c;
		c.len = len;
		for (int i=1; i<=len; ++i) c.d[i]=d[i]*b;
		for (int i=1; i<=len; ++i)
			c.d[i+1]+=c.d[i]/10,c.d[i]%=10;
		if (c.d[c.len+1]) c.len++;
		return c;
	}
	bign operator *= (const int &b){	//重载*=
		*this = *this*b;
		return *this;
	}
	friend ostream& operator << (ostream& output,const bign &x){//重载输出流
		for (int i=x.len; i>1; i--) cout<<x.d[i];
		cout<<x.d[1]-2<<'\n';	//单独处理-2问题
		return output; 
	}
};

int main(){
	int n;
	cin>>n;
	bign f=1;		//int初始化
	for (int i=1; i<=n+1; ++i) f*=2;	//需重载高*低、*=
	cout<<f<<'\n'; 	//需重载输出流
	return 0;
}