二叉树简单总结

一，二叉树的定义

二叉树是一种特殊形式的树结构，二叉树的特点是每个节点最多有两棵子树。

二叉树（Binary tree ）是这样的数结构：它或者是空，或者是由一个根节点加上两棵分别称为左子树和右子树的互不相交的二叉树组成。显然这个定义是递归形式的。

二叉树的一般存储结构采用的是链式存储结构。直观地讲就是将二叉树的各个结点（根节点，叶子节点等）用链表的形式连接在一起。这样通过特定的算法就可以对二叉树中的每个节点进行操作。链式存储的二叉树结点的内存结构如图：

如图，二叉树有三个域，其中lchild 和 rchild 为指针域，用来指向该结点的左孩子和右孩子，data为数据域，用来存放该结点的数据。定义二叉树的结点：

typedef struct BiTNode
{
    char data; /*结点的数据域*/
    struct BiTNode *lchild,*rchild;/*指向左孩子和右孩子*/
}BiTNode ,*BitTree;

上述代码定义了一个二叉树的结点类型BiTNode ，也就是说二叉树的每一个结点都属于BiTNode 类型。另外定义了一个BitTree 类型，它就是指向BiTNode 类型数据（对象）的指针类型 变量声明 BitTree t

二，二叉树的遍历

假设我们已经建立了一个二叉树，在应用二叉树结构解决实际问题时，往往要求在二叉树中找到具有某些特征的二叉树结点。或者要求访问二叉树的每一个结点。这就需要设计一个算法，针对二叉树的结构特征来访问二叉树的每一个结点。这个过程就称作为 二叉树的遍历。

二叉树的定义是一种递归的形式，因此可以应用二叉树的这种递归的逻辑结构特性，采用递归的方法遍历这个二叉树。

从二叉树的定义来说，二叉树宏观是由3个部分组成的，即根节点，左子树，右子树。只要完整地遍历了这三各部分，就等于遍历了整棵二叉树。根节点好访问，它就是一个节点。关键是如何遍历左子树和右子树。可以把左子树和右子树看成看成两棵独立的二叉树，因为它们也都是由根节点，左子树，右子树3部分组成的。

根据二叉树遍历的顺序的不同，对二叉树有3种方案：先序遍历，中序遍历，后序遍历。

1，先序遍历

(1)访问根节点，(2)先序遍历左子树 （3）先序遍历右子树

preoderTraverse(Bitree t)
{
	if (t)
	{
		visit(t->data);/*访问根节点*/
		preoderTraverse(t->lchild);/*先序遍历t 的左子树*/
		preoderTraverse(t->rchild);/*先序遍历t 的右子树*/
	}
}

visit()函数的作用是访问指针 t 指向的结点

2，中序遍历

（1）中序遍历左子树 （2）访问根节点 （3）中序遍历右子树

InoderTraverse(Bitree t)
{
	if (t)
	{
		InoderTraverse(t->lchild);/*中序遍历t 的左子树*/
		visit(t->data);/*访问根节点*/
		InoderTraverse(t->rchild);/*中序遍历t 的右子树*/
	}
}

3，后序遍历

(1)后序遍历左子树 （2）后序遍历右子树 （3）访问根节点

PosoderTraverse(Bitree t)
{
	if (t)
	{
		PosoderTraverse(t->lchild);/*中序遍历t 的左子树*/
		PosoderTraverse(t->rchild);/*中序遍历t 的右子树*/
		visit(t->data);/*访问根节点*/
	}
}

例题

题目  用先序序列创建一颗如图的二叉树，并输出字符位于二叉树的层数

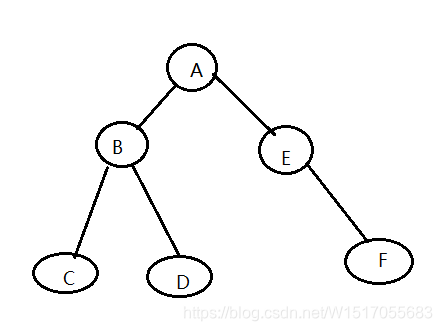
参考代码

#include<stdio.h>
#include<stdlib.h>
typedef struct BiTNode/*结构体定义*/
{
	char data;
	struct BiTNode *lchild, *rchild;
}BiTNode,*BitTree;
/*创建一个二叉树*/
void CreateBitTree(BitTree *t)
{
	char c;
	scanf_s("%c", &c);
	if (c == ' ') *t = NULL;
	else
	{
		(*t) = (BiTNode *)malloc(sizeof(BiTNode));/*创建根节点*/
		(*t)->data = c;								/*向根节点输入数据*/
		CreateBitTree(&(*t)->lchild);				/*递归创建一个左子树*/
		CreateBitTree(&(*t)->rchild);				/*递归创建一个右子树*/
	}
}
/*访问二叉树结点，输出包含D字符结点位于二叉树中的层数*/
void visit(char c, int level)
{
	if (c == 'D')
		printf("%c is at %dth level of BiTTree\n", c, level);
}
/*遍历二叉树*/
void PreOrderTraverse(BitTree t,int level)
{
	if (t)
	{
		visit(t->data, level);
		PreOrderTraverse(t->lchild, level + 1);
		PreOrderTraverse(t->rchild, level + 1);
	}
}
int main()
{
	int level = 1;
	BitTree t = NULL;			/*最开始t指向为空*/
	CreateBitTree(&t);			/*创建二叉树*/
	PreOrderTraverse(t, level);	/*遍历二叉树，找到包含D字符的结点位于二叉树的层数*/
        getche();
}

 

函数PreOrderTraverse() 包含两个参数，一个参数是用来指向二叉树根节点的指针，另一个参数是一个整数变量level ，它的作用是用来记录当前递归操作的层数，也就是记录当前遍历到二叉树的层数，level作为一个局部变量每次作为参数传递时都要加1，因此递归深入自动增1。而一旦递归从下一层返回到上一层，上一层的level值任然保持原来的值不变，因为level传递仅仅是单向值传递，并不是指针传递，它在每一层中的局部值都不会受到下一层任何操作的影响。所以变量就是标记着当前访问的结点位于该二叉树中的层数。