《现代电力电子学与交流传动》读书笔记（九）

本读书笔记分成两部分，书籍原句摘抄和知识整理，本章感悟。

书籍原句摘抄和知识整理
引言
本章研究由电压型逆变器及周波电流器供电的绕线转子和永磁同步电机的控制和估计问题，介绍同步机的标量控制和矢量控制技术，讨论同步机的有传感器和无传感器传动。
9.2 正弦波SPM同步电机传动
同步电机的转速只与逆变器或周波变流器供电电源的频率有关，要不不运行，要不以同步速运行；两种控制方式：一种开环控制，一种自控方式。
9.2.1 开环电压/频率控制
$$T_e=3(\frac{P}{2})\frac{{\Psi }_s{\Psi }_f}{L_s}sin\delta$$


启动后A点，增加负载转矩A-B，增加频率B-C，也可以降低负载转矩到D点，减速路线，D-E-F-A
9.2.2 自控方式
特性：

1. 电子换向取代机械换向。
2. 由于是自控的，没有传统电机稳定性和振荡的问题。
3. 瞬态响应与直流电机相同。
4. 电流$I_s$和磁链${\Psi }_f$间的相角按需要可通过延迟控制环节加以调节。
5. 采用高能磁体，可以使转子惯量更小。
   基于以上优点同步机几乎采用自控的方式。

9.2.3 绝对位置编码器
光学编码器
带解码器的模拟式旋转变压器

9.2.4 矢量控制
矢量控制向量图如下：

转矩表达式：$$T_e=\frac{3}{2}(\frac{P}{2}){\hat{\Psi }}_f{i}_{qs}$$

弱磁方式
弱磁控制的向量图

弱磁控制转矩-速度曲线

正弦波SPM同步电机的矢量控制（包含弱磁区）

9.3 同步磁阻电动机传动
9.4 正弦IPM电动机传动
IPM电机的转矩由两个分量组成：

1. 磁链引起的转矩分量；
2. 磁阻引起的转矩分量。
   $$T_e=\frac{3}{2}(\frac{P}{2})({\Psi }_{ds}{i}_{qs}-{\Psi }_{qs}{i}_{ds})$$
   式中，P是极数，${\Psi }_{ds}={\hat{\Psi }}_f+L_{ds}{i}_{ds}$,${\Psi }_{qs}=L_{qs}{i}_{qs}$,${\hat{\Psi }}_s=\sqrt{{\Psi }_{ds}^2+{\Psi }_{qs}^2}$
   也可以表达：
   $$T_e=\frac{3}{2}(\frac{P}{2})[{\hat{\Psi }}_f{i}_{qs}+(L_{ds}-L_{qs})i_{ds}{i}_{qs}]$$
   与SPM电机类似，IPM电机可以在直接启动或开环V/F速度控制下，但必须要有阻尼绕组。但在自动方式下，电机不需要阻尼绕组。
   最大转矩/电流矢量控制（MTPA）
   采用MTPA电机效率最优。
   定义基准转矩为$T_{eB}=\frac{3}{2}(\frac{P}{2}){\hat{\Psi }}_f{I}_b$
   式中基准电流$I_b=\frac{{\hat{\Psi }}_f}{L_{qs}-L_{ds}}=I_f\frac{I_{dm}}{L_{qs}-L_{ds}}$
   电机的虚构励磁电流$I_f$被认为是恒定的
   $$T_e(pu)=\frac{T_e}{T_{eB}}=\frac{i_{qs}}{I_B}-\frac{i_{ds}}{I_B}.\frac{i_{qs}}{I_B}$$
   或是
   $$T_e(pu)=i_{qs}(pu)[1-i_{ds}(pu)]$$
   式中，$i_{qs}(pu)=\frac{i_{qs}}{I_B}$,$i_{ds}(pu)=\frac{i_{ds}}{I_B}$
   恒转矩的运行曲线
   
   实现MTPA的定子分量随转矩的变化曲线
   
   基于MTPA的IPM电机速度控制系统框图
   
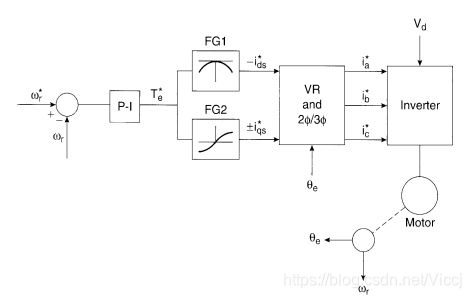
   以上是书上的方式，这里介绍另一种MTPA：
   为了找到电流与转矩的最佳匹配，用下面公式求极值：
   $$T_e=\frac{3}{2}(\frac{P}{2})[{\hat{\Psi }}_f{i}_{qs}+(L_{ds}-L_{qs})i_{ds}{i}_{qs}]$$
   $$i_s=\sqrt{i_{ds}^2+i_{qs}^2}$$
   利用数学中的拉格朗日定理，引入辅助函数
   H = i d s 2 + i q s 2 + λ { T e − 3 2 ( P 2 ) [ Ψ f + ( L d s − L q s ) i d s ] i q s } H=\sqrt{i^2_{ds}+i^2_{qs}}+\lambda\{T_e-\frac{3}{2}(\frac{P}{2})[\Psi_f+(L_{ds}-L_{qs})i_{ds}]i_{qs}\} H=ids2​+iqs2​ ​+λ{Te​−23​(2P​)[Ψf​+(Lds​−Lqs​)ids​]iqs​}
   接着开始拉格朗日求极值的过程
   $$\frac{\partial H}{\partial i_{ds}}=\frac{i_{ds}}{\sqrt{i_{ds}^2+i_{qs}^2}}+\frac{3}{2}\lambda (\frac{P}{2})(L_{qs}-L_{ds})i_{qs}=0$$
   $$\frac{\partial H}{\partial i_{qs}}=\frac{i_{qs}}{\sqrt{i_{ds}^2+i_{qs}^2}}+\frac{3}{2}\lambda (\frac{P}{2})(L_{ds}-L_{qs})i_{ds}=0$$
   $$\frac{\partial H}{\partial i_{\lambda }}=T_e-\frac{3}{2}(\frac{P}{2})[{\psi }_f+(L_{ds}-L_{qs})i_{ds}]i_{qs}=0$$
   对上式进行求解，得到了直轴电流$i_{ds}$和交轴电流$i_q$的关系(MTPA2),然后带入上面的转矩公式中，得到(MTPA1).
   $$i_{qs}^4.{\Delta }_L^2+T_n.i_{qs}.{\hat{\psi }}_f-T_n^2=0with{T}_n=\frac{T_{ref}}{\frac{3}{2}.(\frac{P}{2})}(MTPA1)$$
   $$i_{ds}=\frac{{\psi }_m-\sqrt{{\psi }_m^2+(2\Delta L.i_{qs})}}{2\Delta L}(MTPA2)$$

弱磁控制
IPM电机的有效气隙更小，这使得励磁电感变大，也就是电枢反应的影响很大。这意味着定子电流对定子绕组（${\Psi }_s$）链路的弱磁有更强的影响。可以使电机在基速${\omega }_b$之上运行。
在采用PWM方式电流控制的恒转矩区域中，随着电机转速增加，CEMF也将成比例增加，因而需要更高的供电电压。
在方波模式下，得到定子电压峰值与稳态下相电压的$v_{ds}$和$v_{qs}$存在下面的关系：
$${\hat{V}}_s=2V_d/\pi$$
$${\hat{V}}_s=\sqrt{v_{ds}^2+v_{qs}^2}$$
$$v_{qs}={\omega }_e{{\Psi }_{ds}}^{\prime }+{\omega }_e{\hat{\Psi }}_f$$
$$v_{ds}=-{\omega }_e{\Psi }_{qs}$$
导出一个椭圆方程的形式
$$\frac{(i_{ds}-C{)}^2}{A^2}+\frac{i_{qs}^2}{B^2}=1$$
式中，$A=\frac{2V_d}{\pi {\omega }_e{L}_{ds}}$是长轴的长度；$B=\frac{2V_d}{\pi {\omega }_e{L}_{qs}}$是短轴的长度；$C=-\frac{{\hat{\Psi }}_f}{L_{d}s}$是椭圆中心相对于$i_{ds}$轴的偏移量。
由上式看出，椭圆的中心是固定的，但椭圆的大小随着${\omega }_e$增大而减小。

对于工作点1或者椭圆外任何工作必须落在椭圆内，否则电流控制失效。
考虑工作点2所对应的电流需求，可以把$I_{qs}^{\ast }$给定减少至工作点3.(在恒功率区削弱定子磁链${\Psi }_s$，即削弱CEMF以使电流控制在基速之上仍然有效)。
注意工作点3可得转矩比工作点1要大一些。

以上是书上用PI调节器实现弱磁的方式，另一种方式：
第一步：$${\Psi }_{max}=\frac{V_{max}}{{\omega }_e}$$
进而计算出最大磁链的平方${\Psi }_{max}^2$
第二步：$${\Psi }_q=L_q{I}_{qmtpa}$$
进而计算出Q轴磁链的平方${\Psi }_q^2$
第三步：由$${\Psi }_{max}^2={\Psi }_q^2+{\Psi }_d^2$$和$${\Psi }_{max}^2=(L_q{I}_q{)}^2+({\Psi }_m+L_d{I}_d{)}^2$$导出$$I_{dfw}=-\frac{{\Psi }_m}{L_d}+\frac{\sqrt{{\Psi }_{max}^2-{\Psi }_q^2}}{L_d}$$
第四步：如果$I_{dfw}$比$I_{dmtpa}$小，则需要弱磁。
第五步：弱磁；重新计算$I_{dfw}$和$I_{qfw}$
如果$I_{dfw}$比IGBT最大电流小，$I_{dfw}$就不变，否则$I_{dfw}$等于IGBT最大电流；
如果转矩$T_e$为负，则$I_{qfw}$乘-1变号，否则不变；
按上述的椭圆公式计算计算$I_{dfw}$和$I_{qfw}。
关于IPM的另一种控制方法的详细代码在我的另一篇博文

https://blog.youkuaiyun.com/Viccj/article/details/106273341

9.4.3 定子磁链定向的矢量控制

如上图，电机工作区可分成两部分：恒转矩区和恒功率区，分界线取决于母线电压$V_d$。
基于铁损是磁链和频率的函数。给出磁链-速度关系式如下
$${\Psi }_s=\frac{V_s}{{\omega }_r}={\omega }_e{\Psi }_{sr}={\omega }_e{\psi }_f$$
式中${\Psi }_s$为定子磁链；${\Psi }_{sr}$是额定功率$T_{er}$的定子磁链；${\Psi }_f$为励磁磁链；${\omega }_b$是基速；${\omega }_r$为转速。


电枢反应磁链：$${\Psi }_a=\frac{{\hat{\Psi }}_a}{\sqrt{2}}=\frac{1}{\sqrt{2}}\sqrt{(L_{ds}{i}_{ds}{)}^2+(L_{qs}{i}_{qs}{)}^2}$$
磁链${\Psi }_a$和${\Psi }_f$合成定子磁链${\Psi }_s$，${\Psi }_s$被定向在与$d^e$轴成$\delta$角的方向。
在新的坐标系中的公式：
$$T_e=\frac{3}{2}(\frac{P}{2})({\Psi }_{ds}^{e^{{}^{\prime }}}{I}_T+{\Psi }_{qs}^{e^{{}^{\prime }}}{I}_M)$$
式中，注意${\Psi }_{ds}^{e^{{}^{\prime }}}={\hat{\Psi }}_f$,${\Psi }_{qs}^{e^{{}^{\prime }}}=0$
或
$$T_e=\frac{3}{2}(\frac{P}{2}){\hat{\Psi }}_s{I}_T$$
对于负转矩，角度$\delta$和有功电流$I_r$也是负的，此时磁链三角形移动到第四象限。
绕组励磁式同步电机的磁链${\Psi }_s$由励磁电流控制，因此电机始终工作在单位功率因数下。但对于IPM电机，磁链由定子的滞后电流分量$I_M$控制，因此工作在滞后功率因数下。

反馈信号的处理：
1. 由位置信号通过查表的方式完成单位矢量信号（$cos{\theta }_e和sin{\theta }_e$）的合成。
2. 定子磁链估计($V_d^{{}^{\prime }}和V_q^{{}^{\prime }}$)
转子凸极产生的电感饱和导致直轴和交轴间存在非常复杂的耦合。
建模和仿真采用如下公式：
$$V_q^{{}^{\prime }}={\omega }_b{\Psi }_{qs}={\omega }_b{i}_{qs}{L}_{qs}$$
式中$L_{qs}=L_{qs0}-\frac{i_{ds}}{B}-\frac{i_{qs}}{C}-\frac{i_{ds}^2}{D}-\frac{i_{qs}^2}{E}-\frac{i_{ds}{i}_{qs}}{F}$
且有$$V_d^{{}^{\prime }}={\omega }_b{\Psi }_f+{\omega }_b{L}_{ds}{i}_{ds}$$
式中，${\omega }_b{L}_{ds}$为恒值，
且有${\omega }_b{\Psi }_f={\omega }_b{\Psi }_{f0}+\frac{i_{ds}}{H}+\frac{i_{qs}}{I}-\frac{i_{ds}^2}{J}+\frac{i_{qs}^2}{K}+\frac{i_{ds}{i}_{qs}}{L}$上式中所有常量取决于实际使用的电机。电压$V_d^{{}^{\prime }}和V_q^{{}^{\prime }}$分别代表基速${\omega }_b$时对应的磁链分量。上式表明参数$L_{qs}和{\Psi }_f$是$L_{ds}和L_{qs}$的函数,但$L_{ds}$实质是恒定的。
3. $i_a和i_b$的$V{R}^{-1}$变换($i_{ds}和i_{qs}$)
$$i_{ds}=i_{a}sin{\theta }_e-\frac{1}{\sqrt{3}}(i_a+2i_b)cos{\theta }_e$$
$$i_{qs}=i_{a}cos{\theta }_e+\frac{1}{\sqrt{3}}(i_a+2i_b)sin{\theta }_e$$
4. 磁链的温度补偿
$V_d^{{}^{\prime }}和V_q^{{}^{\prime }}$磁链公式都需要温度补偿，这是因为高能$NbFeB$磁体具有约0.1%/${}^{o}C$的负温度系数。补偿公式为$$V_d=V_d^{{}^{\prime }}+K_d(75^o-T_R)$$$$V_q=V_q^{{}^{\prime }}[1-K_q(75^o-T_R)]$$式中$T_R$为转子温度，由下面的一阶热模型给出；$$T_R(n)=T_R(n-1)+\frac{1}{\tau }[T_S(n-1)-T_R(n-1)]$$
带转子温度补偿的定子磁链表达式如下：
$${\hat{V}}_b={\omega }_b{\hat{\Psi }}_s=\sqrt{V_d^2+V_q^2}$$
5. 转矩和$\delta$角的估计
$$T_e=\frac{3}{2}(\frac{P}{2})\frac{1}{{\omega }_b}(V_d{i}_{qs}-V_q{i}_{ds})$$
$$sin\delta =\frac{V_q}{{\hat{V}}_b}$$
$$cos\delta =\frac{V_d}{{\hat{V}}_b}$$
9.4.3.2方波(SW)模式下的弱磁控制

9.4.3.3 PWM-SW模式的切换

9.5 梯形波SPM同步电机传动系统
9.6 绕组励磁式同步电机传动系统
9.7 无传感器控制
9.7.1 梯形波SPM电机的无传感器控制
9.7.2 正弦波SPM电机的无传感器控制
9.7.2.1 电机端电压和电流检测法
由电机端的电压和电流信号估计获得单位矢量信号，基于此实现定子磁链定向的矢量控制已在上图作了解释。下图是电机的向量图，基于下下框图，其估算的公式如下：
$${\Psi }_{ds}^s=\int (v_{ds}^s-R_s{i}_{ds}^s)\mathrm{d}t$$
$${\Psi }_{qs}^s=\int (v_{qs}^s-R_s{i}_{qs}^s)\mathrm{d}t$$
$${\hat{\Psi }}_s=\sqrt{{\Psi }_{ds}^{s^2}+{\Psi }_{qs}^{s^2}}$$
$$cos({\theta }_e+\delta )=\frac{{\Psi }_{ds}^s}{{\hat{\Psi }}_s}$$
$$sin({\theta }_e+\delta )=\frac{{\Psi }_{qs}^s}{{\hat{\Psi }}_s}$$
$${\omega }_e=\frac{\mathrm{d}{\theta }_e}{\mathrm{d}t}=\frac{(v_{qs}^s-i_{qs}^s{R}_s){\Psi }_{ds}^s-(v_{ds}^s-i_{ds}^s{R}_s){\Psi }_{qs}^s}{{\hat{\Psi }}_s^2}$$
式中$cos({\theta }_e+\delta )和sin({\theta }_e+\delta )$是单位矢量信号。$d^s和q^s$轴上的电流和电压信号分别有电机相电压和相电流通过坐标变换方程得到。
注意，无论是SPM或是IPM电机传动系统该控制策略都适用，但只有当电机运行在最低转速（一般为5%基速以上）时，电机的反电动势足够大时，才适用。


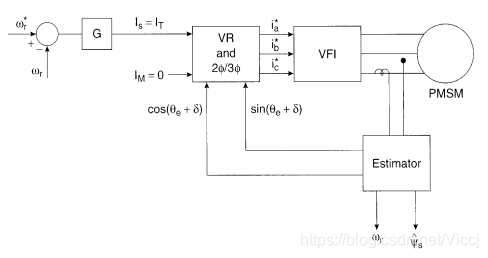
9.7.2.2 电感变化（凸极）效应法
原理是IPM每相绕组的自感将随着转子的位置变化而改变，因此，通过获取相电感值就可以获得转子的位置信息。
IPM电机的相同步电感可以由瞬时电压和电流信息进行计算获得，也可以直接由下式估算：
$$L_{sa}=\frac{v_a-e_a-R_s{i}_a}{\frac{\mathrm{d}{i}_a}{\mathrm{d}t}}$$
式中$$\frac{\mathrm{d}{i}_a}{\mathrm{d}t}=\frac{\Delta i_a}{\Delta t}=\frac{i_a(t_2)-i_a(t_1)}{\Delta t}$$
$$e_a=K{\omega }_e=K\frac{{\theta }_{\mathrm{e}}{i}_a}{\mathrm{d}t}=K[\frac{{\theta }_e(t_2)-{\theta }_e(t_1)}{\Delta t}]$$
时间$t_1$和$t_2$是相连的两个采样时刻。

9.7.2.3 扩展卡尔曼滤波（EKF）的状态估计法
9.8 开关磁阻电机传动系统
9.9 小结
本章首先讨论单个电机或多个电机并联的开环电压/频率控制方案，然后介绍了矢量控制和以弱磁方式扩展运行速度。最后介绍了无传感器控制和SRM的控制。
自我感受

1. 同步电机的控制与异步电机的控制大同小异，开环电压/频率和矢量控制的结构几乎完全相同。
2. 因为同步特性，转子磁链位置不在是难度了，转而介绍无位置传感器的算法。