#C语言 函数实现求两个数的最大公约数

  首先从题干中我们可以看出，本题要求我们构造一个函数实现函数求解两个数的最大公约数，题目如下：

题目要求我们的程序输入两个整数，然后输出的则是这两个整数对应的最大公约数，在完成这道题之前，我们首先要掌握函数的使用方法，在C语言中，其实函数随处可见。在我们的认知中，函数可以写作f（x），而在C语言中，函数的写法其实和这个也差不多，像很典型的printf（），这便是一个很常见的函数，这是C语言中自带的函数，但是在我们日常的敲代码的时候，很多函数其实需要我们自己构建，然后实现对应的功能，这样能够节省我们代码的占用的空间，也能充分减少我们的时间。那么让我们来看看这个程序的代码：

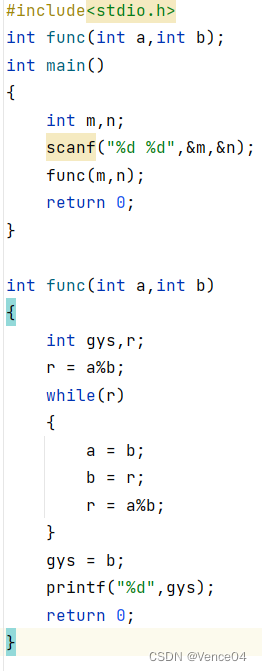
在这其中我们可以看到我们的代码里有一个主函数，还有一个 func函数，这个函数就是求最大公约数的函数，在有函数调用的程序中，有全局变量和局部变量，通俗地来讲，全局变量指的是在主函数中的变量，而局部变量是在函数体内的变量。在这个函数中我们用到了辗转相除法来求两个数的最大公约数，两个数相除，如果有余数的话，那么再用原来的除数再除这个余数，循环这个过程直到余数为零，此时就取余数为零时的那个除数作为两个数的最大公约数，原理很简单，程序内部其实代码也并不复杂，如果能够知道这个方法，那么能够很快就把这个程序给构建出来。