力扣——关于二叉树的问题解析

一.二叉树的前序遍历

解析:1.二叉树的前序遍历是按照根，左子树，右子树的顺序来访问，本题的根访问只输出根结点的数据域

2.二叉树问题多用递归解决，非递归的方式即是递归工作站的原理

3.使用递归时要注意递归结束条件和如何将一个大问题转换成多个小问题

int Treesize(struct TreeNode *root)//计算二叉树的结点个数
{
    if(root==NULL)
        return 0;
    return 1+Treesize(root->left)+Treesize(root->right);
}
void _preorderTraversal(struct TreeNode *root,int *array,int *i)//先序遍历法
{
    if(root==NULL)
        return;
    array[*i] = root->val;
    (*i)++;//必须传的是i的地址,否则递归回来i的值并不会改变还是递归前的值
    _preorderTraversal(root->left,array,i);
    _preorderTraversal(root->right,array,i);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
    int size = Treesize(root);
    int *array = (int *)malloc(sizeof(int)*size);
    int i = 0;
    _preorderTraversal(root,array,&i);
    *returnSize = size;
    return array;
}

因为本题要求我们将二叉树结点的值保存到数组中输出，所以首先我们要求出二叉树的结点个数才能为数组申请空间，要求我们的返回值是一个数组，所以我们建立_preoderTraversal函数用先序遍历法访问树，每输出一个根的值，i++这里要特别注意的是i必须是指针形式，否则在递归时i的值并不会增加，当递归返回时i的值并没有保存下来，用一个指针可以很好的解决这个问题

二.单值二叉树

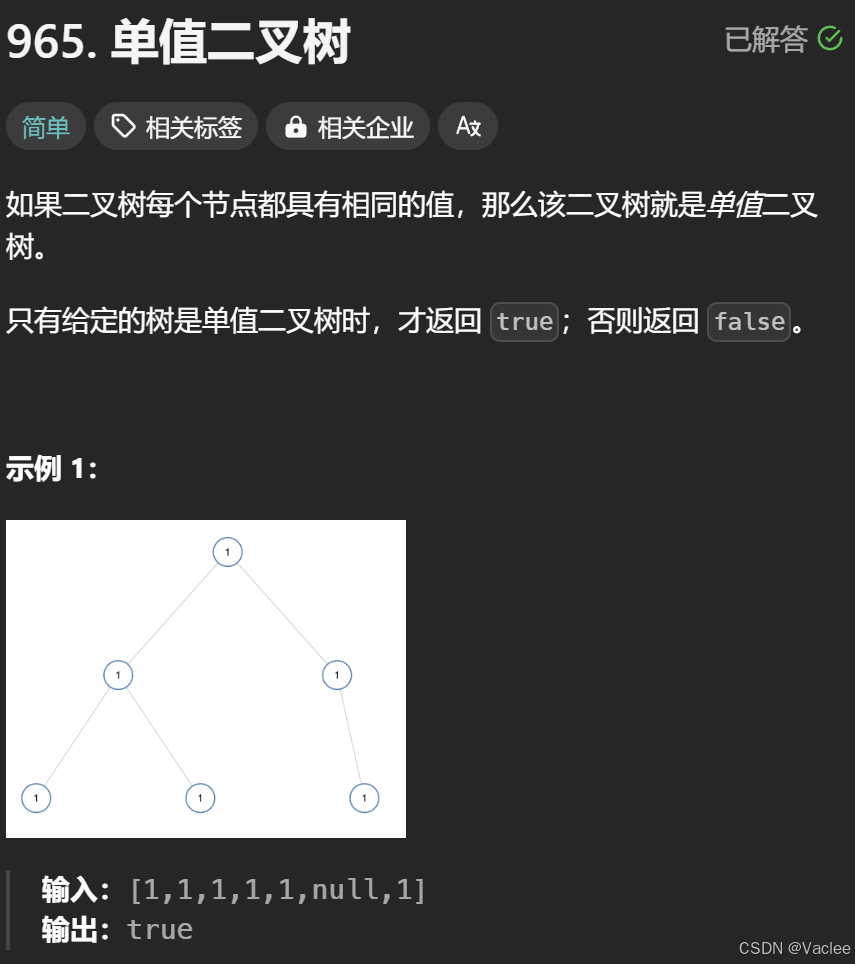
解析:1.我们可以将一个树看成多个树来解决问题，将问题缩小

2.划分为多个树后我们只需要比较左子树和右子树是否相等

3.用递归遍历树如果不相等返回false

bool isUnivalTree(struct TreeNode* root)//运用递归思想
{
    //解题思路:将一颗树分为左右子树，将大问题化为多个小问题解决
    if(root==NULL)
        return true;
    if(root->left&&root->left->val!=root->val)
        return false;
    if(root->right&&root->right->val!=root->val)
        return false;
    return isUnivalTree(root->left)&&isUnivalTree(root->right);
}

首先我们判断根是否为空，为空则说明左子树与右子树都为NULL返回true，然后分别比较根与左右子树的数据域是否相同，不同则返回false，最后递归左右子树遍历整个二叉树

三.二叉树的最大深度

解析:1.用后续遍历，从下到上逐层计算层数

2.同样将树看成多个左子树和右子树

3.如果比较左子树和右子树深度，深度大的层数加一

int maxDepth(struct TreeNode* root) 
{
    if(root==NULL)
        return 0;
    int left = maxDepth(root->left);
    int right = maxDepth(root->right);

    if(left>right)//用函数递归的话，每一次调用都要遍历 复杂度太高
        return left+1;
    if(left<right)
        return right+1;
    return right+1;//这里写成left+1也可以，当左右子树深度相同给任意一边加都可以
}