什么是光学系统模型/光阑/光瞳？超透镜的视场角怎么定义？

我们通常用“物面-入瞳-出瞳-像面”来描述光学系统，为了建立一个高度抽象、统一且强大的分析模型。这个模型将所有光学系统的核心功能统一到同一个框架下，将可能由十几片透镜组成复杂的光学结构“黑盒化”，极大地简化了设计、分析和沟通的过程。

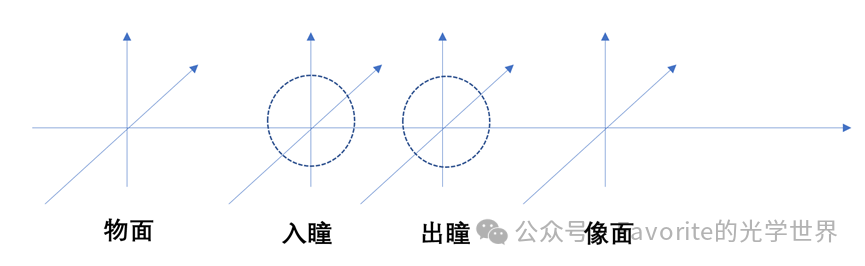
物面：这是光线的起点，是我们要观察或测量的物体所在的理论平面。它代表了信息的源头。

入瞳：这是从物方看过去，孔径光阑所成的像。入瞳决定了有多少光线能从物面发出并进入系统。它是系统在物方的“虚拟窗口”。

出瞳：这是从像方看过去，同一个孔径光阑所成的像。它决定了有多少光线能从系统射出并到达像面。它是系统在像方的“虚拟窗口”。

像面：这是光线的终点，是物面通过光学系统所成的像所在的理论平面。它代表了信息传递的目的地。

入瞳与出瞳都理解都需要正确认识一个概念——孔径光阑：物理上限制进入系统光束粗细的元件（如相机中的光圈叶片）。

这个模型天然地定义了评价光学系统性能的几个最基本参数：

视场：物面上有多大范围可以被成像。它由入瞳的位置和大小以及第一个光学元件的尺寸共同决定。

相对孔径 / F数：决定系统集光能力和分辨率的关键参数。F/# = 焦距 / 入瞳直径。

景深：物体在前后移动时，在像面上仍能保持清晰成像的范围。景深的计算完全依赖于入瞳的直径。

光瞳衔接：在复杂系统中（如显微镜+相机），前一个系统的出瞳必须与后一个系统的入瞳匹配，才能避免光线损失（渐晕）和成像问题。

同时，这个模型为我们提供了分析像差的“坐标系”

孔径相关像差（如球差）：与通过入瞳不同高度的光线有关。

视场相关像差（如畸变、彗差）：与物点在物面上的不同位置有关

用这个模型来描述光学系统，我们就能抓住所有光学系统共有的“输入-处理-输出”关系，从而为我们设计、分析和交流光学系统提供了一个无比清晰和有效的工具。

在有物理的孔径光阑的情况下，引入“瞳孔/瞳面”（入瞳/出瞳）的概念，正是为了简化分析，提供系统级的视角。对于物体发出的光线来说，它“看不到”系统内部复杂的透镜和光阑，它只“看到”一个虚拟的入瞳。任何能指向入瞳的光线就能进入系统，任何不能指向入瞳的光线就会被阻挡。切记“瞳面”是孔径光阑的“虚拟投影屏幕”，而不是光阑本身，它是光学系统中像差定义和测量的基准面。

如此，我们可以定义一些概念：

物方数值孔径 (NA) :由物点和入瞳边缘的连线角度决定。

视场角 (Field Angle) :由物点中心与入瞳中心的连线角度决定。

波像差（Wavefront Error）：实际波前与一个理想球面波前在出瞳面上的光程差。泽尼克多项式（Zernike Polynomials）就是在出瞳这个圆形域上对波像差进行拟合和分解的。

如何理解孔径光阑对孔径角的约束呢？

————————————————————

对于有限远的物体，我们关心的是“从物点出发，能进入系统的最大张角”。

对于无限远的物体，物体发出的光线是平行光。此时，我们关心的是“一束多粗的平行光能被系统接收？” 这个“粗度”的衡量标准，就是系统的入瞳直径。通过直接设定入瞳直径或F数，就等效于约束了系统的孔径角。

如何理解入瞳位置对视场角的定义？

—————————————————————

视场角本质是物点主光线与光轴的夹角。入瞳在物面后方，表示各物点发出的主光线“发散”至入瞳。入瞳在物面前方，则代表主光线在到达物点前已通过入瞳，物点位于入瞳的“光线延长线上”，主光线从物点“反向会聚”至入瞳。无论入瞳在物点前/后，物高与入瞳中心连线始终定义视场角。

在光学设计和分析中，孔径光阑始终被建模为一个平面，即使其物理实体可能是曲面。当我们在光学设计软件中将一个面设置为“光阑”时，软件在计算光线追迹时，只考虑该面的通光孔径在切线平面上的投影。软件在计算入瞳/出瞳的“理想位置”时，使用的是“近轴瞳孔”的概念，而近轴光线本身是没有任何像差的理想化光线。因此，计算出的入瞳/出瞳是一个位置、大小都完全确定的理想化几何平面。而真实的光学系统一定是有像差的，这也就产生了光瞳像差。简单来说，就是系统的“虚拟窗口”本身不是一个完美的、无像差的像。

当存在光瞳像差时，会有入瞳/出瞳形状失真（入瞳或出瞳的像可能不再是规则的圆形，可能会变成椭圆形、彗星状或其他不规则形状）、入瞳/出瞳位置漂移（入瞳的位置会随着视场角的变化而变化，而不是固定在一个点上。意味着对于视场边缘的点，其入瞳发生了移动和变形）及光程差不等（从物点出发，通过这个有像差的入瞳不同部位的光线，到达像面的光程不再相等）的问题存在。

渐晕：由于光学系统中透镜框、光阑等机械元件的遮挡，导致偏离光轴（即视场边缘）的物点发出的光束不能完全通过系统，从而使得成像光束的有效口径随着视场角的增大而逐渐减小的现象。

让我们把这些概念串起来，想象光线是一次跨国旅行：

入瞳是出发机场的护照检查关口，没有护照和签证（光线没指向入瞳），你绝对上不了飞机。但即使你通过了检查（光线指向入瞳），不代表你一定能到达目的地（像面）。飞机可能会故障备降（渐晕）。

孔径光阑可看作是航班的总座位数，它决定了理论上最多有多少人能同时旅行。

渐晕可理解为航行过程中的各种意外，比如某个乘客在转机时被拦下（被透镜框遮挡）；飞机遭遇气流被迫抛掉部分行李（能量损失）。

出瞳可理解为目的地机场的入境大厅，所有最终成功抵达的旅客（成像光线），必定是从这个大厅出来的（其反向延长线通过出瞳）。但这个大厅里显示的所有航班信息（完整的出瞳），包含了所有起飞了的航班。有些航班可能中途返航了（被渐晕），这些旅客并没有真正从这里出来。

因此，光线通过入瞳和出瞳是成像的必要不充分条件。

说完了孔径光阑和瞳面，我们再来看看视场光阑和入射窗/出射窗

视场光阑：物理上限制成像范围（视场大小）的机械孔径。它决定了物面（或像面）上有多大区域能最终被看到。光线超过这个范围的物体，其光线会被视场光阑完全阻挡，无法到达最终的像面。

入射窗：视场光阑被其前面的所有光学元件所成的像。如果物点位于入射窗之内，它发出的光线有可能通过系统；如果在外，则肯定被视场光阑遮挡。

出射窗：视场光阑被其后面的所有光学元件所成的像。

引入这两个“窗”的概念，其根本目的与引入“光瞳”的概念完全相同：为了将复杂的光学系统“黑盒化”，建立一个简单、统一的分析模型，从而极大地简化对视场、渐晕和光线限制的分析。对于物空间某个点能否成像，只需判断该物点是否位于入射窗之内。如果在内，则能成像；如果在外，则不能。

Q 对于超表面（特指超透镜）而言，它的入瞳/出瞳在哪？视场角怎么定义？

超透镜自身通常同时充当着“透镜”和“孔径光阑”的双重角色。其物理边界就是限制光束大小的那个孔径。因为它是一个非常薄的元件，其前后几乎没有光学系统来为这个孔径“成像”。因此，超透镜的入瞳和出瞳，在理论上都与其自身的物理孔径平面重合。

超透镜的可用视场角通常是一个性能权衡的结果，而不是一个清晰的几何边界。这是因为超透镜由无数个特定方向的纳米结构（纳米柱）组成。这些结构对光的散射特性具有方向依赖性。当光线以极大的倾斜角入射时，纳米结构无法提供设计所需的相位延迟，导致波前调控失效，成像质量急剧下降（如效率降低、像差增大）。而超透镜的设计通常针对正入射（On-axis）光线优化。离轴（Off-axis）的物点会引入巨大的波像差，特别是彗差(Coma) 和像散(Astigmatism)。这些像差会随着视场角的增大而迅速恶化，使得边缘视场变得模糊不清。因此工程师会定义一个“衍射效率高于某个值（如20%）”或“MTF曲线高于某个对比度”的视场范围作为其有效视场角。

‍文章转载：Favorite的光学世界

免责声明：转载此文目的在于传递更多信息，仅供读者学习、交流之目的。如有侵权，请联系删除！