华容道问题求解_详细设计(三)之查找算法1_DFS

原创

于 2024-03-07 18:09:36 发布 · 1.2k 阅读

23 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #深度优先 #华容道81步解法 #DFS #Dijkstra 应用

本文详细介绍了使用深度优先搜索(DFS)解决华容道问题的过程，包括堆栈操作、布局快照的保存、图的构造以及如何通过Dijkstra算法找到最短路径。后续章节提到BFS方法的改进效果。

（续上篇）
使用DFS查找算法的原因是因为它符合本人的思考习惯，另外在第一版时用的就是这个方法，后来知道这不是查找这类问题的最好方法。
在前面的概要设计中的框图里描述的方法就是DFS，它可以找到一个解法，时间可能比较快。（不一定，看运气）

DFS算法基本要素分析

DFS 深度优先算法，核心是采用堆栈结构存贮中间过程。其特点是后进先出，从而也决定了其所谓深度优先的特点。即后续情形都是最先处理，因此就会沿着一条路径探索下去，到达终点后，才返回去处理没有处理过的。画出图来，它的过程就像一个触角一样，伸到最远处，再回退继续执行类似的过程，不但探索知道全部探索结束。

堆栈操作分析

 堆栈中应该保存一个当前的布局，如图示：
 这是初始布局
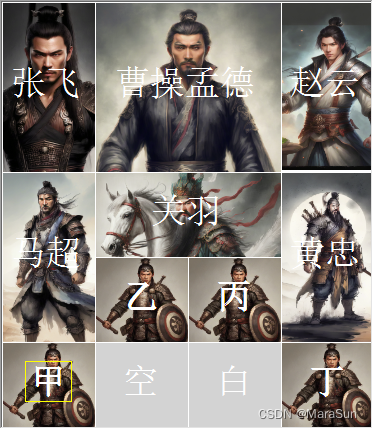
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/direct/1e773af73fd346c3ac5d062745e2ddc7.png)
 移动一个棋子如下
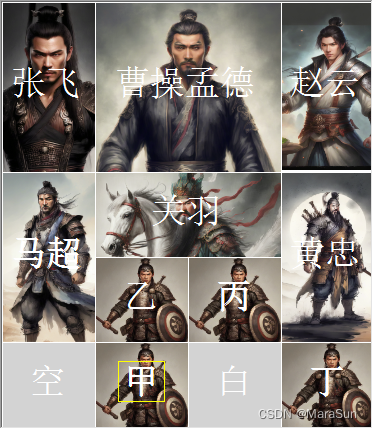
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/direct/c9e3023e86ef4afa9035c4768c220519.png)
 假设此时不能继续移动，那么应该返回到上一个场景；也就是说在移动棋子之前，初始布局需要入栈，到当前的无路可走状态（假设），需要做出栈处理。出栈后，需要恢复之前的布局，也就是棋子的位置。因此必须要引入当前布局的一个快照，我这里称之为状态，同时为了便于对相同的局面进行判断，也需要引入一个当前局面的指纹作为记录。当然这个指纹可以是一个hash 值。
 经过上述分析，我们要得到当前布局的快照和一个hash 值用来记录这个快照。
 说明：非常容易犯一个错误，就是把当前的布局实例进行入栈操作，这个看起来好像很对，但是实际上由于入栈操作对对象而言，保存的是一个引用，因此后续操作会影响堆栈里的那个保存的对象属性（其实就是同一个实例而已）。因此必须要克隆一个当前布局的实例，将这个克隆的实例入栈。另外在出栈时，还要将它映射回去到当前的布局中。
 根据上面的思路，有关堆栈相关的代码如下：
 首先，在设置初始布局的函数中的最后部分，进行了堆栈的初始化

     private void _setDefayultLayout()
     {
   
   
    	......

         //CurPiece = _gameState.pieces[0];
         // push the initial state onto the  stack 
         SearchOpenPieces(); // 查找可以移动的棋子
         StateShot stateShot = new StateShot(gameState, 0);//克隆当前局面的快照
       
         var stVertexLst = new List<Piece>{
   
    gameState.pieces[2],gameState.pieces[3], gameState.pieces[4], gameState.pieces[5] };//记录可能的起始节点，这里指的是图结构的起点，后面会述及。
         //################################################
         //##                 初始化堆栈                  ##
         //################################################
         
         InitStateStack(stateShot, stVertexLst);//初始化堆栈
     }

为了提高效率，先找到可以移动的棋子，即 open piece，把这个数据也保存到堆栈中，这样出栈后，就不用再计算了。

构造一个图

因为DFS找到的结果不一定是最佳方法，因此要想办法找到求解最佳路径的方法。理论上，上面的算法应该是遍历了所有的场景，如果把这些场景看做是一个节点那么可以想见这个查找方法实际上是可以构造出一个图来的。只要知道起始点和终点，利用现有的最短路径算法，例如 Dijkstra 算法，就可以找到最佳方法（最短路径）。因此下面的问题是如何建立这个图。
图的两个要素，一个是节点一个是路径。显然节点可以考虑用每个布局的hash 值来表示，而路径是两个节点确定的，如果是加权路径，还有个路径的长度。在华容道的经典步骤中，实际上是不考虑路径长度的。只考虑动作，不考虑这个动作的开销，因此在这个图中如果按照传统的手工走法，只要将每条路径的权重设为一样就可以利用最短路径算法找出来和人工移动一致的最佳步数。如果权重不一样，例如将移动一格（一个单位正方形）的权重设为1，移动两格的权重设为2，利用最短路径算法就可以找出来移动距离最少的解法（有人把这种方法算作是最佳方法）。
构造一个图的具体步骤，在堆栈的进出过程中，有一步是必须要做的，就是重复步骤的判断。可以想见，如果移动时，碰到重复的走法，这个走法应该放弃，否则就会陷入死循环当中。用图来考虑，就是这个节点已经存在了，但是路径应该是新的，因此对于重复的布局，只要将路径加上就可以了，这样到全部步骤结束（栈空）时，这个所有节点和路径就都有了，图的数据结构也就建好了。
另外，华容道的解法布局，我们是知道的，即曹操的在出口的位置就是完成了一个解；然而此时其他棋子的位置我们是不知道，因此在构造图的终点节点时，需要做个特殊判断。
根据上述分析，得到如下代码