MATLAB代码:基于条件风险价值的合作型Stackerlberg博弈微网动态定价与优化调度
关键词:微网优化调度 条件风险价值 合作博弈 纳什谈判
参考文档:《A cooperative Stackelberg game based energy management considering price discrimination and risk assessment》完美复现
仿真平台:MATLAB yalmip+cplex+mosek
主要内容:代码主要做的是一个基于合作型Stackerlberg博弈的考虑差别定价和风险管理的微网动态定价与调度策略,提出了一个双层能源管理框架,实现多个微网间的P2P能源交易,上层为零售商的动态定价模型,目标是社会福利最大化;下层是多个产消者的合作博弈模型,优化各产消者的能量管理策略。
同时,采用纳什谈判法对多个产消者的合作剩余进行公平分配,还考虑了运行风险,采用条件风险价值(CVaR)随机规划方法来描述零售商的预期损失。
求解方面,双层模型被基于KKT条件转换为单层模型,模型可以高效求解。
这段代码是一个基于合作型Stackelberg博弈的微网运行策略的程序。它包含了多个功能和工作,涉及到的主要内容如下:
-
模型参数设定:定义了一系列参数,包括产消者/零售商的购电和售电、交易上下限、电负荷、风电出力、风电场景概率等。
-
决策变量初始化:定义了一系列决策变量,包括交易量、储能容量状态、充放电功率等。
-
零售商/领导者的约束条件:定义了零售商的约束条件,包括购电和售电的范围限制、平均购电价和平均售电价的限制等。
-
产消者/跟随者的约束条件:定义了产消者的约束条件,包括电功率守恒、总交易量守恒、交易量上下限、储能容量状态等。
-
KKT条件对偶约束:定义了KKT条件中的拉格朗日乘子,并给出了相应的约束条件。
-
KKT条件互补松弛:引入了Big-M法处理割平面约束,定义了一系列布尔变量,并给出了相应的约束条件。
-
单层目标函数:定义了目标函数,通过强对偶定理消去双线性项,并求解最小化目标函数。
-
数据分析与画图:对求解结果进行了数据分析和可视化展示,包括交易的绘制。
总体而言,这段代码实现了一个基于合作型Stackelberg博弈的微网运行策略,通过优化决策变量来实现最小化目标函数,以达到合理的能源管理和交易策略。它涉及到的知识点包括优化算法、线性规划、约束条件等。
这段代码是一个基于合作型Stackelberg博弈的微网运行策略的求解程序。它包含了多个决策变量和约束条件,用于计算微网的运行成本和交易策略。
首先,代码导入了一些常数参数,如购电、售电、交易上下限、电负荷等。这些参数用于定义微网的运行环境。
然后,代码定义了一系列决策变量,包括辅助变量、能量交易量、储能设备充放电量、储能容量状态等。这些变量用于描述微网的能量管理策略。
接下来,代码导入了一系列约束条件,包括能量平衡约束、交易量约束、能量充放电约束、储能容量约束等。这些约束条件用于限制微网的运行行为,确保其满足能量需求和稳定性。
然后,代码定义了目标函数,即微网的运行成本。目标函数包括了产消者的能量交易成本和风险调度成本。
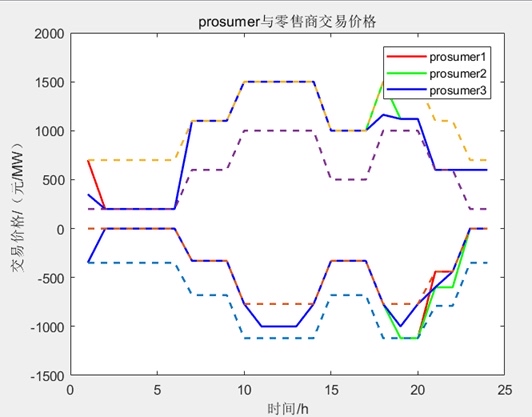
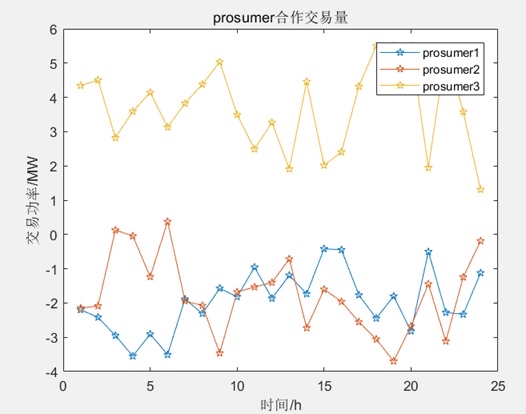
最后,代码使用求解器对目标函数进行求解,得到微网的最优运行策略和成本。求解结果包括了产消者之间的合作交易量、产消者与零售商的交易等。
代码还包括了一些数据分析和画图的部分,用于可视化展示微网的运行策略和结果。
总的来说,这段代码实现了一个基于合作型Stackelberg博弈的微网运行策略的求解程序,通过优化决策变量和约束条件,求解微网的最优运行策略和成本。它涉及到了数学优化、博弈论、能量管理等知识点。
这段程序主要是一个基于合作型Stackelberg博弈的能源管理的求解程序。它通过考虑差别定价和风险评估来优化微网的运行策略。下面我将逐步解释程序的各个部分。
首先,程序开始时进行了一些初始化操作,包括清除变量、关闭所有图形窗口等。
然后,程序定义了一些决策变量,包括三个产消者的各个场景的转移支付,即C_epay_1、C_epay_2和C_epay_3。
接下来,程序导入了一些常数变量,包括P_trading、C_Non和C_trade。这些变量分别表示交易量、非交易成本和交易成本。这些变量的值是从外部文件中加载的。
然后,程序定义了三个产消者的风电场景概率,分别为pai_1、pai_2和pai_3。
接着,程序对一些变量进行了处理。首先,将C_Non和C_trade中的负号去除,并将其转换为成本(负数代表获得收益)。然后,根据公式23计算了每个产消者的贡献度,即alpha_1、alpha_2和alpha_3。这些贡献度表示每个产消者对总交易量的贡献程度。
接下来,程序初始化了一些保存优化结果的矩阵。
然后,程序进入一个循环,循环求解每个场景。在每个场景中,程序构建了一个约束矩阵C。约束矩阵包括了公式21和公式22的约束条件,以及一个等式约束条件。公式21表示交易成本和转移支付不能超过非交易成本,公式22表示三个产消者的转移支付之和为0。
接着,程序定义了目标函数TC_benefits。该目标函数是一个关于转移支付的函数,通过最大化该函数来优化的效益。
然后,程序配置了求解器的一些参数。
接下来,程序使用求解器对约束矩阵C和目标函数TC_benefits进行求解计算。如果求解成功,程序将保存求解结果。否则,程序将报错。
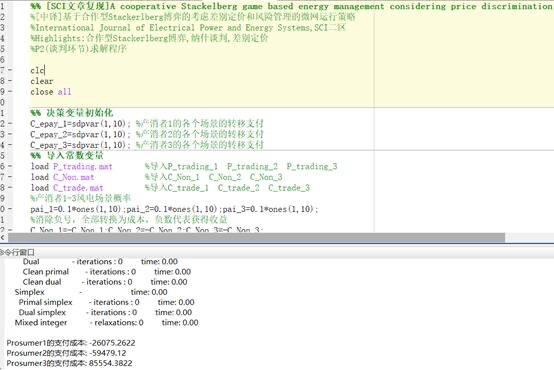
最后,在所有场景求解完成后,程序输出了运行结果。输出结果为每个产消者的支付成本。
综上所述,这段程序主要是一个求解基于合作型Stackelberg博弈的能源管理的优化问题的程序。它涉及到了数学优化、线性代数、概率论等知识点。通过对约束条件和目标函数的建模,程序能够找到最优的转移支付方案,从而优化的效益。






















 444
444

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








