数据结构与算法笔记：动态规划之LCS,0/1-Knapsack,Transitive-Closure,All-Pair-Shortest-Path

动态规划 Dynamic Programming(DP)

引语

• 从上一篇文章中我们知道了为什么要做动态规划以及它是怎么一回事
• 动态规划基于原本递归的算法(效率低，会引起指数爆炸)，倒过来
• 递归是把原本复杂的事情变得简单，而动态规划是从最基础最简单的事情开始
• 从基础打起，一层一层很有耐心的把它算出来
• 也就是由几种子任务的递归结构转化成递推结构，换句话说
• 从递归的思路开始，不要扔掉它，它会给你一个解决方案(逻辑上的计算方式)
• 在真正实现的时候，把它倒过来计算，仅此而已

LCS: Longest Common Subsequence 最长公共子序列

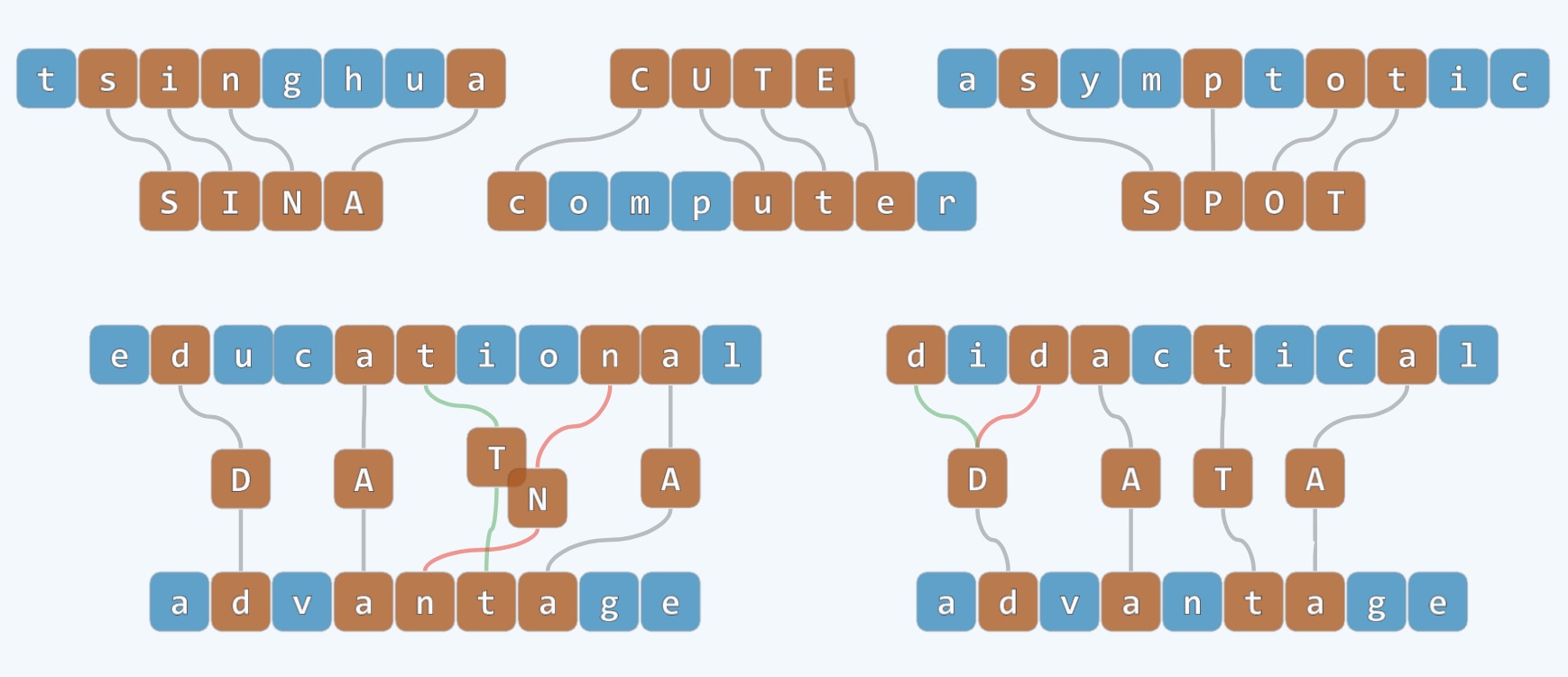
• 我们这里考虑的序列是字符串序列(string sequence)
• 某一天你可能会遇到两个string的问题, 每个string中元素都是有顺序的
• 如果你可以任意从中挑出几个字符排列起来，这样得到的序列就相对于之前序列叫做子序列
• 给你一对序列，从中分别抽出一些字符作为子序列，有时候非常的巧
• 挑出的两个子序列中含有相同的字符，我们称之为公共子序列, 显然这是取决于运气的
• 有的时候很容易得到，有的时候很难得到，有的时候完全没有公共子序列，我们要研究的是公共子序列的最长者
• 而有的时候最长的公共子序列可能包含多个，如上图的DATA和DANA，长度都是4
• 同时我们看到由顺序问题和多种选择引起的歧义，如上图下半部分的两图，所以我们先收敛一下
• 我们的问题主要是专注研究任何一对足够长的序列，在其中找出最长的子序列, 如何寻找呢？
• 我们倒过来看，我们有两个序列A和B, 不失一般性，A短，B长，无所谓的
• 它们末尾的末元素(字符)X，我们问一个问题，它俩是一样的么？答案肯定有两种：一样和不一样
• 如果一样，就在其前面切一刀，如下图所示，把它降解为更小的一个任务，前后任务长度差1
• 比如，我们要求didacticA和advantA的公共子串, 只需要再求didactic和advant的公共子串即可
• 这种情况，我们通过减而治之的方式来求解
  
• 如果不一样，也就是最后两个字符不同，这时候我们通过分而治之，把原来的任务分解为两个子任务
  
• 其中一个任务是，把一个字符串的末字符砍掉，另一个字符串的末字符保留
• 另一个任务是，把一个字符串的末字符保留，另一个字符串的末字符砍掉
• 如上图所示，把原先一个任务被分解为两个子任务了
• 这样的话最终的公共最长子串可以从这两个子任务中得到，只需要在二者之间取一个最大者即可
• 我们无非就是做上面的减而治之和分而治之来把最终的问题解决掉
• 从大体来看，我们可以把两个字符串通过坐标的形式来展示，坐标原点在左上角
• 如下图所示，有两个例子，任选其一即可
  
• 这么对齐来看的话，我们可以看到有一个矩阵，矩阵的每一个格子都对应一个子任务
• 一般而言，对于一个第i行，第j列的格子，用d(i,j)来表示，我们可以从坐标上得到两个新的字符串
• 横向的是0 ~ j的字符串，纵向上是0 ~ i的字符串，换句话说，我们只需要计算这两个新的字符串的LCS即可
• d(i,j)上LCS问题的解，从逻辑上来说就是这样的
• 如果我们要计算最左下角格子，也即是最终的任务(原始两字符串的LCS)
• 要考虑三种情况，一种是向上的，一种是向左的，一种是沿对角线方向(右下->左上)的递归
• 这些可能取决于A[n](A字符串的末字符)和B[m](B字符串的末字符)是否能够匹配
• 从递归上来说，会有子任务生成出来，会造成可怕的指数爆炸，这是逻辑上可行的
• 方法我们有了，我们要转过来，求助于递推，因为对于任何两个字符串，我们都会有递归基(递推基)
• 我们知道第一行都是0，从第二行开始才会有相应的值，我们可以用一种填表的方式来完成矩阵的填写
• 矩阵本身就是一个look-up table, 我们通过这些天然的递推基(字符串上的字符)
• 就可以给自己下面，右面，对角线(左上->右下), 提供一个offer, 每个格子都会考虑这个offer
• 如果offer更好，我们就会选择它，这个递推的方式可以理解沿着对角线(斜着(左下-右上)一条一条的划线，就像是BFS一样)
• 实际上更简单的方式是可以沿着矩阵的横线(或竖线)一行一行(一列一列)的来算，比如，我们一行一行的来算
• 比如进行到了d(i,j)的格子，它的offer来自三个方向(上方，左方，左上方)，即d(i-1,j-1),d(i-1,j),d(i,j-1)
• 当我们计算到d(i,j)的时候，为它提供offer的三个格子都已经计算就绪了，只需要进行对比，取最大值
• 如果最大值来自于左上角的一个格子，那么还需要加上一个1(这个方向是减而治之的情况，末字符匹配被减除，很好理解)
• 而其他两个方向的格子是分而治之得来的，对结果本身没有什么贡献，只是简单的继承过来
• 从这个意义上来说，我们计算最终的长度是几，就会有几次的减而治之，但是减而治之通常会有歧义，上面也说过
• 不过通过这种算法，我们都可以将所有可能覆盖，不会遗漏

0/1-Knapsack 背包问题

• 任何一个背包问题的输入都是由两列等长的数字组成，一个是v,一个是w
• 假设有一个场景，你出门旅行，带个背包，背包有个承受重量限度W，里面可以装很多东西
• 每一个物件都有一个重量，用w表示，同时这件东西对你的价值用v来表示
• 问题是，在给定的v和w两个序列，你有一个背包，最优(价值最大化)带走物品的方案是什么？
• 形式上来说:
  • Given{vi>0 ∣ 1≤i≤n},{wi>0 ∣ 1≤i≤n}Given \{ v_i > 0 \ | \ 1 \leq i \leq n \}, \{ w_i > 0 \ | \ 1 \leq i \leq n \}Given{vi​>0 ∣ 1≤i≤n},{wi​>0 ∣ 1≤i≤n} and W > 0, find a subset K of [1,n] s.t.
  • ${\sum }_{k\in K}{v}_{k}ismaximizedwhile{\sum }_{k\in K}{w}_k\le W$
• 我们拿到这个问题，可能会立即想到贪心的方法(实际上没法奏效)，举个例子，比如你有4件东西
  
• 它们的重量和价值都是一样的，四件的值分别是2，6，5，4，而背包容量是9，如何选择最优方案呢？
• 贪心无非两种方式：先贪最大的或先贪最小的
  • 如果先贪最大的，塞进去了6，那么5和4都不能放，只能选择2了
  • 从而装下的价值是6+2=8<9, 但是我们知道这个方法不是最优的
  • 因为我们明显能看到5+4=9，正好填满背包
  • 如果从小的开始贪，会碰到同样的甚至更尴尬的问题：2+4=6<9
  • 所以贪心策略并不合适
• 如何解决呢？我们还是需要一个递归的方法，回到之前的那张表上去，如上上图
• 每个格子都会在y轴对应一个最大值(该格子对应最上面一行数字中的一个数字)，代表了背包允许的最大值W
• 以该格子为起点, 在与y方向平行的v和w列中, 在y方向上会有以这个该格子所对应v,w为界的一个(v,w)前缀
• 这个格子所对应的子任务就是某一个重量的上限W, 在这个意义上来说，如果允许你装的物品不是所有的
• 而是其中前几项，此时所能得到的最大解(最优解)，就是我们装包的方案
• 这个方法最开始也是来自于递归，我们要把每个问题作为一个子问题来不断进行递归
• 如果上图比较抽象，可以将上面的表格简化为下面的矩阵
  
• 在这里$v_i,w_i$表示第i项的价值和重量，同理$v_{i-1},w_{i-1}$是第i-1项的，此两项相邻
• 如上图所示，第i项中的一个格子表示：允许背包最大值是W，前i项最佳的装包方案是m[i][W]
• 这是一个二维矩阵，用二维数组来表示，下标分别为：W和i($v_i,w_i$)
• 按照刚才的语义，对于第i项的一个格子，可以分而治之，其实也就是考察它前面的两个问题($m[i-1][W-w_i],m[i-1][W]$)
• 这两个问题，都是对应于第i-1行的，第i-1行相对于第i行，区别就在于，第i项物品能不能装，答案有两种：选择第i项，不选择第i项
  • 如果没有考虑第i项，这种方案最优的在第i-1行来说对应的就是第i行正上方的$m[i-1][W]$
  • 正上方解的特点是它们位于同一列，背包所允许的容量没有变化都是W
  • 因为没有选择第i项，所以最优的解来自于同样背包容量下的第i-1项所得到的解(这个解暂时还没得到，但通过递归可以得到)
  • 如果考虑了第i项，那么现在把第i项减除(为了得到第i项的子任务，第i-1项的情况)，对应于只考虑前i-1项的问题
  • 这个问题对应就在第i-1行，而且它的列要从之前的W移动到W-$w_i$的位置，也就是$m[i-1][W-w_i]$这个格子
  • 总结来说，这个问题可以根据你在第i项出现之后所做的选择(选或不选)可以递归的分而治之为两个子问题
  • 这两个子问题如果可以递归得到，我们要做的时候就是在合并的时候把两者的最优解中的更大者保留下来即可
    
• 我们可以通过一个例子来说明，如上图，随便找一个格子，比如红框里的160作为第i行的一个最优解
• 它此时对于的W是21，而它对应物品(比如记该物品代号为p)的v,w分别是39,9
• 此时这个最终的160取决于两种情况, 选择了物品p，和不选择物品p
  • 如果选择了该物品p, 那么它的子任务就要从21-9=12，在第i-1行中的12对应的格子是121
  • 因为用了这个物品，所以这个121+39=160(我们的最大价值)，12+9=21(等于背包最大容量)
  • 另一种情况是不选择该物品p, 隐藏在160的正上方, 其值是149 < 160, 所以最终选择160，舍弃149
• 上图中每一个格子都是这样的例子，因为是递归的解法，它会向正上方和左上方减而治之，同样会造成指数爆炸
• 这时候我们就可以通过D.P.的逆向思维，从第一层算起，比如上图的第一项物品，其v,w是(42,4)，在背包允许容量达到4之前
• 它能装的东西为0(不能装任何东西), 当到达了4的重量，就可以装下第一项物品了
• 然后再往后不管W再怎么增大也只能装下这一件物品，因为当前只有这一件物品
• 有了这个基础的解之后，我们就可以算出第2行, 第3行, …
• 于是通过递推的方法把上表中所有的行每个单元的解一个不落地求出
• 如果我们指定任意一个W, 可以通过查阅该表中指定的W所对应的最后一行的那个格子就是能用所有物品情况下得到的最优解
• 这个填表的递推的方法，其实就是我们的动态规划，其实它的缺陷也很明显，时间复杂度太高了
• 如果我们有n件物品，背包最大限度是W, 那么意味着我们要把这个矩阵填完，其时间复杂度不会低于O(n * W)
• 在这里我们为了避免麻烦，把W取整处理，即便如此，我们的W是很难控制的，如果它很大，也会爆炸，虽然不是指数爆炸
• 虽然存在爆炸的可能，但是比之前递归减而治之的指数爆炸好太多了，我们要保证W不要太大
• 这个背包问题也可能有很多的变种，其基本套路都是基于这个0/1背包问题

Transitive Closure: Definition 传递闭包

• 这是图论中的一个东西，它主要研究有向图，在有向图中，每条边都是有方向的，表示一个点通过一条边到达另一个点
• 但是到达并不限于直接到达，如果有一个点，经过一条有向边，再经过一条有向边，再经过一条有向边，沿途所经过的任何一点
• 可以认为它是直接或是间接的抵达，我们把抵达这个概念，不管直接或间接，我们都称作抵达，如果是这样
• 我们希望在两者之间再引入一条边，如上图红色的边，我们的任务是: 要给每个间接到达的点增加一条红色的边，那怎么做呢？
• 我们可以把任意一个有向图用一个矩阵来表示，每个单元格子，比如d(i,j)代表第i行和第j列，单元格中存1或0表示是否存在一条边
• 这个矩阵不是对称的，从i到j有一条边并不代表重j到i也有一条边，否则就是无向图了

• 如上图所示，每一个步骤都有左右两个矩阵，一开始左边是空的，因为还没有开始
• 在逐层的计算过程中原来的1都会保留下来，不会变成0，因为它意味着直接可达，接下来随着计算的推进会引入新的为1的单元
• 也就是0会翻转为1, 1不会翻转为0, 当计算进行到最后的时候，如上图(17)的两个矩阵左边的矩阵是原输入矩阵，右边的矩阵是最终的Closure
• 在这个Closure中新增的边都是那些红边(代表的是间接可达)，问题是如何计算出这些红边？
• 如果是间接到达的，如上上图所示，从u到v, 意味着中间可能要经过一些桥梁，假设中间某点k可以作为桥梁
• 以k为桥梁有哪些u可以间接通往v呢? 在上图的矩阵中，可以简化为上上图(左)的描述，假设u行和v列所对应的单元原来不是1(不能直接到达)
• 如果有一个k来帮忙，在对角线上(k行，k列)上对应的是上上图X的位置，而帮忙意味着
  • 一个条件是第u行，第k列是个1(表示u到k可以抵达，不管是直接还是间接)
  • 另一个条件是在k行v列有个1(表示k到v可以抵达，不管是直接还是间接)
• 这样通过(u,k)的1，和(k,v)的1，也就是两个绿色的1创建一个红色的1(也就是直连u,v的红边)
• 从递归的角度来说，如果原来单元格没有1，要考虑是否可以变成1，只需要去看所对应的两个子问题也就是两个绿色格子的1就可以了
• 这个也是分而治之的递归，可以帮助我们思考计算的逻辑，同样的只能解决小规模问题，稍微大的问题就会变成指数爆炸
• 所以，我们还是借助动态规划的递推，我们不是站在(u,v)需要哪些k,而是反过来想k可以给哪些u和v提供offer
• 我们的方式是这样的，我们把k从0号点开始，它作为桥梁能解决哪些点的连接问题，以至1,2,3,…n-1 一直这么下去
• 当所有点解决的时候，自然这个问题也就解决了

关键代码实现

# k作为一个桥梁为每个点对(u,v)提供offer，k有n个
for k in range(0, n)
    # u和v的组合枚举
    for u in range(0, n)
        for v in range(0, n)
            # 这时候我们考虑u,v之间是否连线
            A[u][v] = A[u][v] || A[u][k] && A[k][v]
        '''
        下面的if判断可以忽略，和上面的一个for循环是一个并列的逻辑，算法到上面其实已经够了
        如果A[u][k]是1，我们还需要把A[u]整个一行完全翻转过来的
        写下这个if判断会更快，如果算法语言或硬件机制支持一长串的bitwise位运算的话
        我们现在的硬件条件是64位，一旦矩阵超过64位就要降级为64位处理
        因为每一行都是1,0字符串，如果是64位之内的，都可以用一个字符表示这个64位的数字
        64位乘64位的矩阵就可以转换为64个字(一行一个字)，这时候这个内部循环可以和这个if等价起来
        如果满足条件，可以一下翻转过来一行，从而减少一个内部的for循环
        一般情况下，还是有所改进的，所以推荐使用下面的if判断来代替一个for循环，不过u,v的双重for循环更容易理解一些
        '''

        '''
        if A[u][k]
            A[u] = A[u] | A[k]
        '''

All-Pair Shortest Path 任意两点间最短距离

• 我们来看由此衍生出来的另一个相似问题，最短路径问题，我们之前的最短路径问题如网兜模型是立足于某个单元的最短路径
• 如果是一个城市，每个人活动范围任意，我们需要考虑的是任意两点之间的最短距离，这叫做All-Pair Shortest Path
• 我们基于动态规划给出其中一个算法，这个算法和上面的传递闭包算法很像，传递闭包考虑的问题是u和v之间是否能能够达到
• 我们这个问题考虑的是u和v之间必然能达到，能达到最短的距离是什么，这时候我们也可以用刚才类似的方法
• 如果u和v之间能达到，这时候给出一个特定的解了，但是我们想知道最短的达到距离是多少，我们可以通过桥梁k的形式来枚举计算

关键代码实现

for k in range(0, n)
    for u in range(0, n)
        for v in range(0, n)
            A[u][v] = min(A[u][v], A[u][k] + A[k][v])

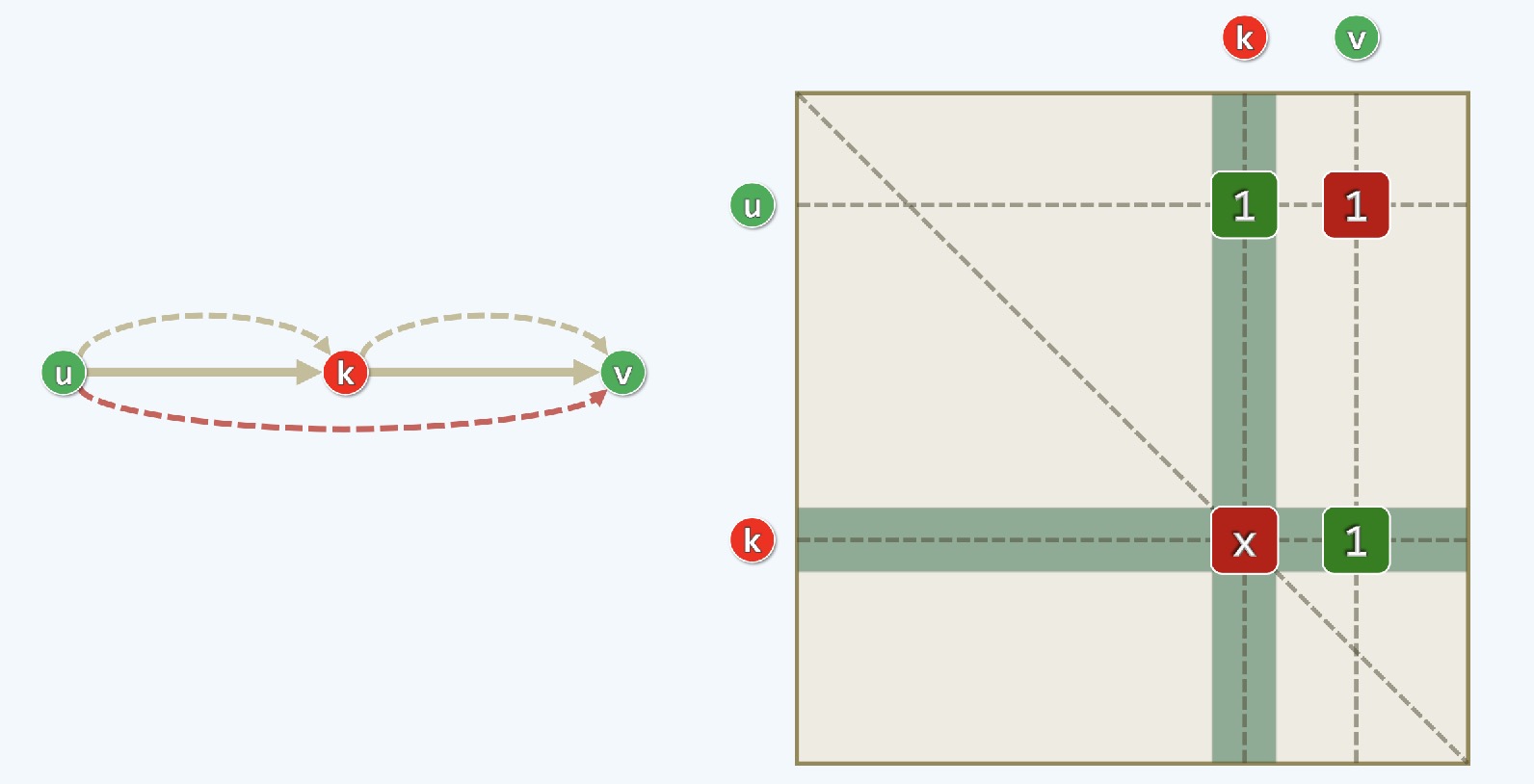
• 如上图所示，u和v之间有一个距离红色的uv,这个值可能很大，我们可以考虑以k为桥梁的其他可能通路来优化这个解
• u要经过k这个桥梁，这样u,k之间有一条通路，距离可以表示为uk, 接下来k到v也有一条通路, 距离记为kv
• 如果这两条路存在，必然构成从u经过k到v的一条新的通路，其距离我们可以记为uk+kv, 这个距离给u,v提供一条新通路的offer
• 如果uk+kv<uv, 那么就可以取而代之，得到新的最优解(最小距离的路径)
• 和之前传递闭包算法一样，通过矩阵移动更新所有单元格，有时候某一单元格中的数字会更新取新的最优解，因为其他桥梁可能提供更优的解
• 当按照动态规划的模式，一个点一个点的作为桥梁完成计算，最后这张表中就会给出最终的解
• 表中任何一个单元中的数值如果是非无穷的话，就是其连接两点之间的最小距离，而空白的单元，默认都是无穷，也就是不可达的点
• 其遍历过程同传递闭包非常类似，因为比较麻烦，此处不再图解！

总结一下

• 我们要知道为什么我们要研究动态规划：效率提升
• 动态规划如何从递归模式倒推过来的：逆向思维
• 从制表，箭头递推等技巧对动态规划的学习非常重要