leetcode669. 修剪二叉搜索树

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例 1：

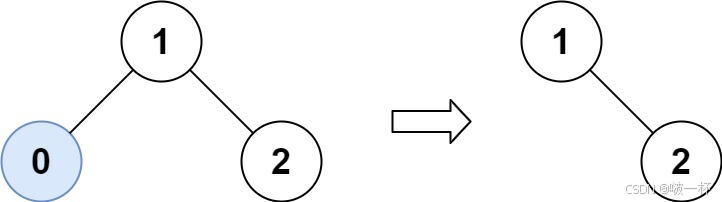
输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]

示例 2：

输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出：[3,2,null,1]

提示：

• 树中节点数在范围 [1, 104] 内
• 0 <= Node.val <= 104
• 树中每个节点的值都是 唯一 的
• 题目数据保证输入是一棵有效的二叉搜索树
• 0 <= low <= high <= 104

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} low
 * @param {number} high
 * @return {TreeNode}
 */
var trimBST = function(root, low, high) {
    if(root == null){
        return null;
    }
    if(root.val < low){
        let right = trimBST(root.right,low,high);
        return right;
    }
    if(root.val > high){
        let left = trimBST(root.left,low,high);
        return left;
    }
    root.left = trimBST(root.left,low,high);
    root.right = trimBST(root.right,low,high);
    return root;
};