算法——KMP算法

刚接触KMP算法的时候觉得很难理解，囫囵吞枣学了一通，现在都忘光光了。重新看了一下。
KMP算法主要用于字符串的匹配=>在一个主串(s)中查找模式串(c)，返回模式串的位置。

以leetcode的一道题为例，以下例子可用kmp算法解答。

实现 strStr() 函数。
给定一个 haystack 字符串和一个 needle 字符串，在 haystack 字符串中找出 needle 字符串出现的第一个位置(从0开始)。如果不存在，则返回 -1。
示例 1:
输入: haystack = “hello”, needle = “ll”
输出: 2
示例 2:
输入: haystack = “aaaaa”, needle = “bba”
输出: -1
说明: 当 needle 是空字符串时，我们应当返回什么值呢？这是一个在面试中很好的问题。
对于本题而言，当 needle 是空字符串时我们应当返回 0 。这与C语言的 strstr() 以及 Java的 indexOf() 定义相符。

蛮力法

按照蛮力法（暴力破解）的思路，分为以下几个步骤：
① 先在主串s中找到模式串中c[0]的位置，假设s[k]=c[0]
② 继续判断s[k+1]和c[1]是否相等，若相等，判断s[k+2]和c[2]是否相等…
步骤②的结束条件为c遍历完成(success)或者存在i(i<c.length)使得s[k+i]!=c[i](fail)
③ 若s[k+i]!=c[i]，c指针重新指向c[0]，s指针指向s[k+1]，继续步骤①

KMP算法

KMP算法通过记忆模式串的前后缀重复度匹配长度，缩短了匹配的时间。

那么kmp如何缩短匹配时间呢?
这得从寻找字符串的最长前后缀说起，假设有模式串ABCABP，那么这个模式串的最长前后缀表如图所示

• 对于模式串的子串A，它的前缀和后缀都是空的，故A下面的值是0
• 对于模式串的子串AB，它的前缀为A后缀为B，没有相同部分，故B下面的值也是0
• 对于模式串的子串ABC，它的前缀为A,AB,后缀为C，BC，没有相同部分，故C下面的值是0
• 对于模式串的子串ABCA，它的前缀为A,AB,ABC，后缀为A,CA,BCA，相同部分为A，长度为1，故填上1
• 对于模式串的子串ABCAB，它的前缀为A,AB,ABC,ABCA，后缀为B,AB,CAB,BCAB，共同部分为AB，长度为2，故填上2
• 对于模式串的子串ABCABP，它的前缀为A,AB,ABC,ABCA,ABCAB，后缀为P,BP,ABP,CABP,BCABP，没有相同部分，故填上0

最长前后缀有什么作用呢？
匹配字符串BKLABCABCHFKK（主串s）和ABCABDG（模式串c）
先画出模式串的最长前后缀表

假设前面的匹配进行顺利，一直匹配到模式串的第六个字符D，它与主串的C字符不匹配，如下图

暴力破解的方法是这样子的，模式串（c）从头0开始匹配，主串（s）从k位置后移一位k+1开始匹配。

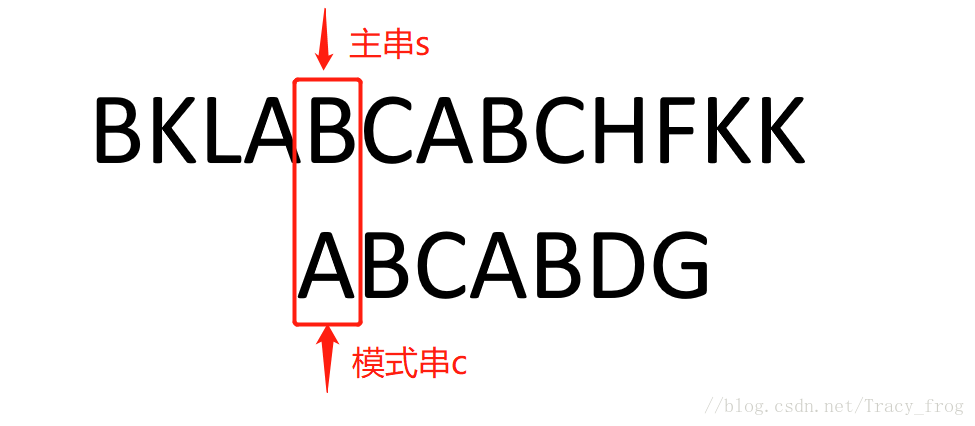
但KMP不是那样，它记忆了模式串的最长公共前后缀长度
通过前面的表我们知道ABCAB的最长公共前后缀长度为2，即字符D前面有两个字符与模式串的前两个字符是一样的（ABCABD），而由于主串ABCAB部分已经与子串ABCAB部分匹配，说明主串ABCAB部分的最长公共前后缀也是AB

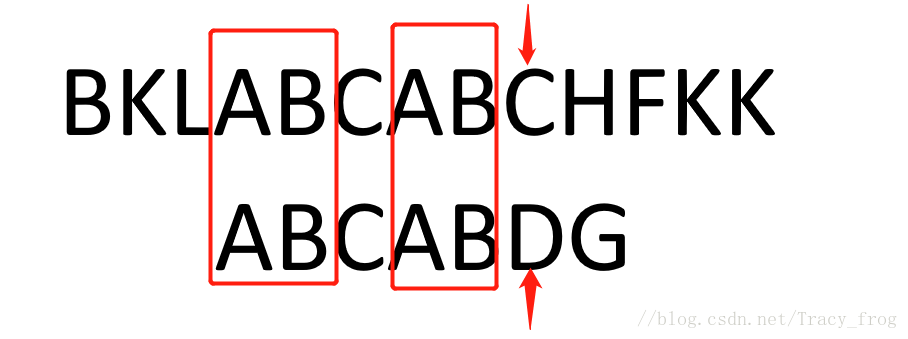
本来暴力破解法，主串得从加粗部分BKLA BCABCHFKK开始找ABCABDG，但现在我们知道BKLABCABCHFKK中加粗部分开头有AB，内部也有AB，我们可以直接把模式串第一个AB移动到与主串第二个AB匹配，那么我们便可以省去很多步。

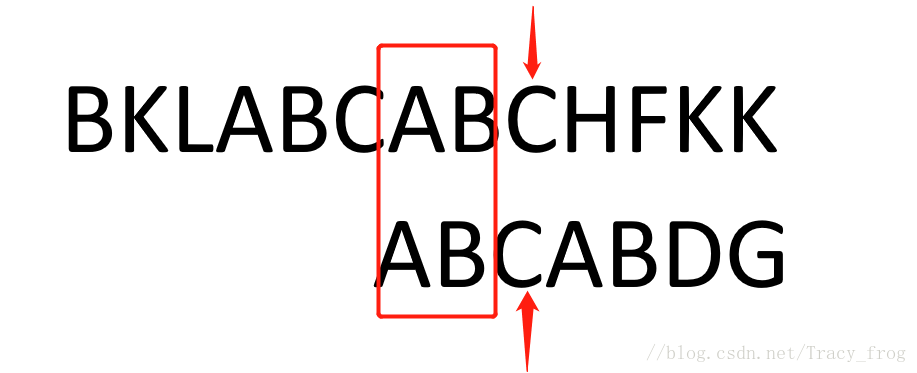
那KMP是怎么做的呢？
KMP算法引入一个next数组，用于存放上述最长前后缀长度，不同的是next[i]指的是前i个字符的最长前后缀长度，next[0]初始化为-1。

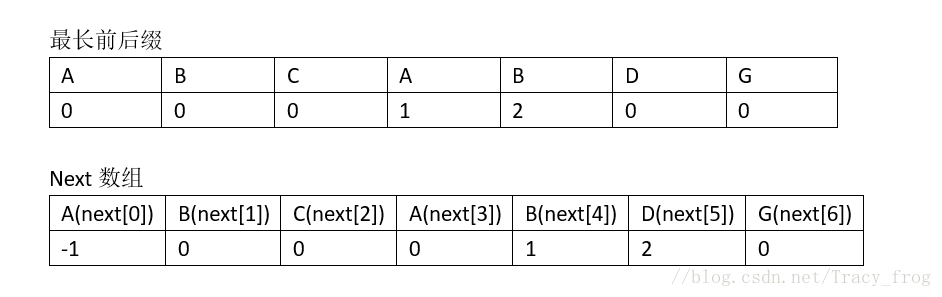
next数组如何求得？(重点！！！)
我们看简单字符串可以很容易得到它的next数组（手动计算），但计算机需要通过指令计算出next数组，如何求next数组呢？
代码如下：

void getNext(char* c,int next[])  //c为模式串
{  
    int len = strlen(c);  
    next[0] = -1;  
    int k = -1;  //前缀
    int j = 0;  //后缀
    while (j < len - 1)  
    {  
        if (k == -1 || c[j] == c[k])   
        {  
            ++k;  
            ++j;  
            next[j] = k;  
        }  
        else   
        {  
            k = next[k];  
        }  
    }  
}  

代码分析：
① 当k==-1时，k+1指向模式串第一个字母c[0]，前缀为空，故next[j+1]=0=-1+1=k+1
② 当c[k]==c[j]时，说明从0-k长度的前缀有对应后缀与之相等，next[j+1]=next[j]+1=k+1
③ 合并①②点可得：

```
if(k==-1||c[k]==c[j])
{
	next[j+1]=k+1;
}
```

④ c[k]!=c[j]时，k要回退到next[k]。这个其实有点难解释。
先看下面这段模式串c
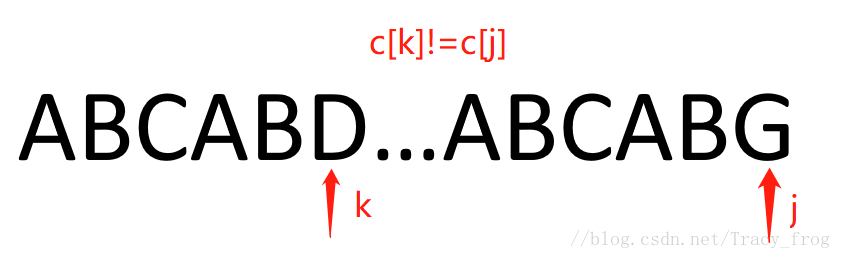c[k]!=c[j]，那么我们便要找尽可能长的匹配长度。

过程：

• 由于c[k] != c[j] (D != G), 令k = next[k] = 2
• c[k] != c[j] (C !=G)，令k = next[k] = 0
• c[k] != c[j] (A != G)，令k = next[k] = -1

递归的思想：

• 我们目标求next[j + 1]，由于此时c[j] != c[k]，next[j + 1] = next[j] + 1的美丽幻想泡汤了，但是前面ABCAB这一串我们已经匹配过了，我们知道c[k]前面字符串是ABCAB，那么next[j]前面必然也会有ABCAB。
• 令k = next[k]，找到上一个公共最长前缀的位置，它与c[j]前面的前缀是匹配的、较次长前缀匹配（原谅我使用这个词，就是虽然没有上一个匹配前缀那么长的，但矮子里拔高个），此时再看c[k]是否等于c[j]，若相等，则我们找到了k的位置，否则继续往前查找更次长公共前缀（第一名不行找第二名，第二名还不行找第三名）。
• 若幸运找到了c[k] == c[j]，则c[j + 1] = c[j] + 1 = k + 1，若不幸没找到，则k最后等于-1，next[j + 1] = 0 = k + 1
  
  KMP代码：

#include<iostream>
using namespace std;
void getNext(int* next, char* c)
{
	int j = 0;
	int k = -1;
	next[0] = -1;
	int len = strlen(c);
	while (j < len - 1)
	{
		if (k == -1 || c[k] == c[j])
		{
			k++;
			j++;
			next[j] = k;
		}
		else
		{
			k = next[k];
		}
	}
}
int KMP(char* s,char* c,int* next)
{
	int j = 0;
	int k = 0;
	int len_c = strlen(c);
	int len_s = strlen(s);
	while (k < len_c && j<len_s)
	{
		if (k==-1 || c[k] == s[j]) // 相等则继续匹配下一个字符
		{
			k++;
			j++;
		}
		else // 不等，移动模式串继续遍历匹配
		{
			k = next[k];
		}
	}
	if (k==len_c)//模式串遍历完才结束的，说明匹配成功
		return j-len_c;
	return -1;
}
int main()
{
	char c[100], s[100];
	char str;
	cin >> c >> s;
	int len = strlen(c);
	int* next=new int[len];
	getNext(next, c);
	cout << "next指针：";
	for (int i = 0;i < len;i++)
		cout << next[i] << " ";
	cout << endl;
	cout << KMP(s, c, next) << endl;
	delete[]next;
	return 0;
}

扩展：
从头到尾彻底理解KMP（2014年8月22日版）