浮点数在内存中的存储

根据IEEE754标准，浮点数V可以表示为：
V = (−1)^S ∗ M ∗ 2^E

• S为符号位，0为正，1为负
• M为有效数字，大于1小于2
• E为指数位

比如5.5，二进制表示为101.1

• S=0
• M=1.011
• E=2

计算机在存储这个5.5时，将这些特征数依次存进内存中，以浮点数的形式读取。
如果以别的形式读取这个数，可能会造成不一样的结果。

对于32位浮点数（float）

S占1bit，E占8bit，M占23bit

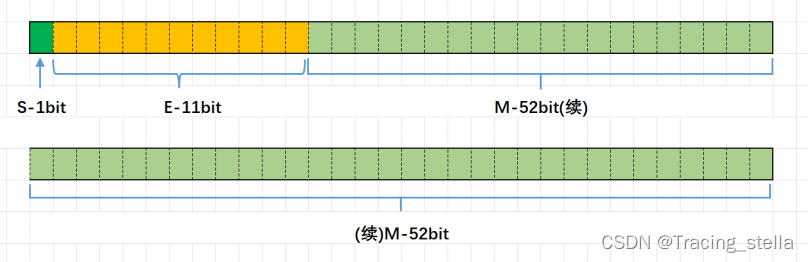
对于64位浮点数（double）

S占1bit，E占11bit，M占52bit

浮点数在存储的过程中，对M和E又有一些特别规定。

计算机存储M时，因M是1.xxxxxxx，即前面的1和小数点是固定不变的，所以计算机只存储后面的xxxxxxx，读取时自动加上前面的1.

计算机存储E时，可能会出现负数，而E为一个无符号整数，取值范围为 0~255 或 0~2047，所以在存储E时，要先加上一个中间数。对于8位E，中间数是127，对于11位E，则是1023。

浮点数在读取时，又要分三种情况。

E不全为0且不全为1

以5.5为例，用float表示为
0 01000001 01100000000000000000000
十六进制表示为
40 b0 00 00

E全为0

这种情况下指数部分为-127，是一个非常非常小的数，此时E就等于-126（-1022），M不再加上第一位的1，而是一个0.xxxxxxx的小数，这是为了表示很小很小的数字。

E全为1

如果有效数字M全为0，则表示无穷大（正负取决于符号位s）