笔记整合一：由线性回归到逻辑回归

最新推荐文章于 2024-05-31 09:00:00 发布

原创

最新推荐文章于 2024-05-31 09:00:00 发布 · 置顶 · 913 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#线性代数 #逻辑回归 #机器学习 #算法

本文介绍了从线性回归到逻辑回归的概念及其转换。线性回归用于连续变量预测，通过最小二乘法和正则化避免过拟合。逻辑回归则通过Sigmoid函数将线性回归结果映射到[0,1]区间，适用于二分类问题。文中还讨论了离散化在逻辑回归中的作用，包括提升模型表达能力、加快计算速度和增强模型稳定性。" 120966712,4956627,使用QT实现网页浏览功能,"['QT开发', '网络编程', 'C++', 'GUI应用']

文章目录

- - 一、相关概念

一、相关概念

1、优化机器学习算法模型参数

1.1 最小二乘法公式：

在这里插入图片描述
观测值就是我们的多组样本，理论值就是我们的假设拟合函数。目标函数也就是在机器学习中常说的损失函数，我们的目标是得到使目标函数最小化时候的拟合函数的模型。

1.2 梯度下降

1、梯度定义：
	微积分中，对多元函数参数求∂偏导数，将求得的各个参数的偏导数以向量形式写出来，即为梯度。
	其本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，
	即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。

2、梯度下降:
	求最小化损失函数，关于损失函数：为了评估模型拟合的好坏，通常用损失函数来度量拟合的程度。
	损失函数极小化，意味着拟合程度最好，对应的模型参数即为最优参数。
	在线性回归中，损失函数通常为样本输出和假设函数的差取平方。
	比如对于m个样本（xi,yi）(i=1,2,...m)（xi,yi）(i=1,2,...m),采用线性回归，损失函数为：

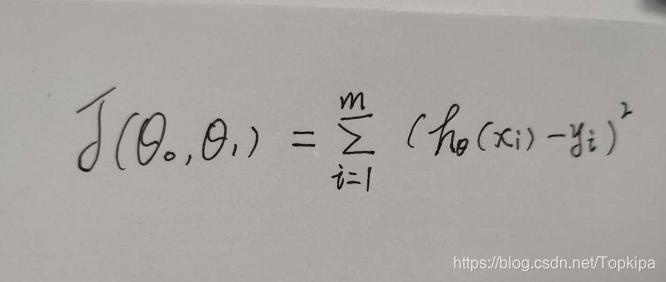
在这里插入图片描述

3、梯度下降算法调优：
（1）、步长选择
（2）、算法参数初始值选择
（3）、归一化：由于样本不同特征的取值范围不一样，可能导致迭代很慢，为了减少特征取值的影响，可以对特征数据归一化，也就是对于每个特征x，求出它的期望和标准差，这样特征的新期望为0，新方差为1，迭代次数可以大大加

最低0.47元/天解锁文章