蓝桥杯笔记(Python程序设计)

最小公倍数和最大公约数模版

def func3():
    a = int(input('please enter 1st num:'))
    b = int(input('please enter 2nd num:'))
    s = a * b
    while a % b != 0:
        a, b = b, (a % b)
    else:
        print("最大公约数是：", b)
        print("最小公倍数是：", s // b)

1. 二进制位数

问题描述
十进制整数 2 在十进制中是 1 位数，在二进制中对应 10 ，是 2 位数。
十进制整数 22 在十进制中是 2 位数，在二进制中对应 10110 ，是 5 位数。
请问十进制整数 2022 在二进制中是几位数？

答案提交
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

思路
这道题对于其他人来说，可能还稍微麻烦了，但是对于python说，几乎秒杀，只需要用python的bin函数，就可以迅速将十进制转成二进制，然后再减去首字母的两个0b即可。

参考答案
 

print(len(bin(2022))-2)

2. 晨跑

问题描述
小蓝每周六、周日都晨跑，每月的 1、11、21、31日也晨跑。其它时间不晨跑。
已知 2022年1月1日是周六，请问小蓝整个2022年晨跑多少天？

答案提交
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

参考答案

import datetime

start = datetime.datetime(year=2022,month=1,day=1) # 定义头为2022.1.1
end = datetime.datetime(year=2023,month=1,day=1) # 尾为2023.1.1
cnt = 0 # 计数
while start != end: # 当没到下一年的时候，也就是遍历2022全年
    if start.isoweekday() in [6,7] or start.day in [1,11,21,31]:
        cnt += 1  # 小蓝每周六、周日都晨跑，每月的 1、11、21、31日也晨跑。
    start += datetime.timedelta(days=1) # 下一天
    
print(cnt)

3. 调和级数

问题描述

小蓝特别喜欢调和级数 S(n)=1/1+1/2+1/3+1/4+…+1/n 。
请问，n 至少为多大时，S(n)>12 ？

参考答案

s = 0
i = 1
while s <= 12:
    s += 1.0/i
    i += 1 
print(i-1) # 不用加最后一次

4.贪心算法

问题描述

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。
对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。
示例 1:
输入: g = [1,2,3], s = [1,1]
输出: 1
解释:
你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
所以你应该输出1。
示例 2:
输入: g = [1,2], s = [1,2,3]
输出: 2
解释:
你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.

题目解析：在这里采用贪心策略的思想，让孩子们按胃口大小排成队，胃口小的在前面，饼干按大小也摞好，小的在上面，每次给队头的孩子一个能满足他胃口且尽可能小的饼干（注：这个过程就是求局部最优解的过程），吃到饼干的队头孩子就离开队伍，直到饼干发完或者队伍没人即每个孩子都吃到饼干（注：这是通过局部最优解堆叠求得全局最优解）

参考答案：

class Solution:
    def findContentChildren(self, g: List[int], s: List[int]) -> int:
        g.sort()#列表的排序命令，默认从小到大排序。将孩子按胃口大小排成队
        s.sort()#把饼干也从小到大摞起来
        child=0#统计吃到饼干的孩子数
        i=0;j=0;
        while i<len(g) or j<len(s):#设置循环结束条件
            if s[j]>=g[i]:#如果第j个饼干刚好可以满足第i个孩子
                child+=1
                i+=1
                j+=1
            else:#如果不能，换下一个饼干试试能不能满足这个孩子
                j+=1
        print(child)

5.穿越雷区（BFS）

参考答案：

n = int(input())
arr = [list(map(str, input().split())) for _ in range(n)]
ex, ey = 0, 0

# 找到起点 'A' 和终点 'B' 的坐标
for i in range(n):
    for j in range(n):
        if arr[i][j] == 'A':
            start = (i, j, '', 0)  # 将起点的坐标、前一步状态、步数添加到队列
        if arr[i][j] == 'B':
            ex, ey = i, j  # 记录终点的坐标

def bfs():
    dir = [(1, 0), (-1, 0), (0, 1), (0, -1)]  # 定义四个方向：下、上、右、左
    visited = set()  # 用集合存储已经访问过的位置
    q = [start]  # 使用列表作为队列，将起点添加进去

    while q:
        x, y, s, step = q.pop(0)  # 从队列中取出一个位置的坐标、前一步状态、步数

        for i, j in dir:
            dx, dy = x + i, y + j  # 计算新位置的坐标

            # 判断新位置是否在迷宫范围内，且没有被访问过，且不等于前一步状态
            if 0 <= dx < n and 0 <= dy < n and (dx, dy) not in visited and arr[dx][dy] != s:
                visited.add((dx, dy))  # 标记新位置为已访问

                # 如果新位置是终点，返回步数
                if dx == ex and dy == ey:
                    return step + 1

                # 将新位置的坐标、前一步状态、步数添加到队列
                q.append((dx, dy, arr[dx][dy], step + 1))

print(bfs())  # 打印最短路径的步数

6.穿越时空之门（进制转化）

【问题描述】
        随着 2024 年的钟声回荡，传说中的时空之门再次敞开。这扇门是一条神秘
的通道，它连接着二进制和四进制两个不同的数码领域，等待着勇者们的探索。
        在二进制的领域里，勇者的力量被转换成了力量数值的二进制表示中各数
位之和。
        在四进制的领域里，力量的转换规则相似，变成了力量数值的四进制表示
中各数位之和。
        穿越这扇时空之门的条件是严苛的：当且仅当勇者在二进制领域的力量等
同于四进制领域的力量时，他才能够成功地穿越。
国王选定了小蓝作为领路人，带领着力量值从 1 到 2024 的勇者们踏上了这
段探索未知的旅程。作为小蓝的助手，你的任务是帮助小蓝计算出，在这 2024
位勇者中，有多少人符合穿越时空之门的条件。

def check(a):
    jin_2, x2 = jin_s(a, 2)
    jin_4, x4 = jin_s(a, 4)
    print(a, x2, x4)
    if jin_2 == jin_4:
        return True
    return False
 
 
def jin_s(x, m):
    res = []
    while x:
        res.append(x%m)
        x //= m
    return sum(res), res
 
 
def main():
    res = 0
    for i in range(1, 2025):
        if check(i):
            res += 1
    print(res, '**************')
# 63
if __name__ == '__main__':
    main()

7.数字串个数（快速幂模版）

【问题描述】
小蓝想要构造出一个长度为 10000 的数字字符串，有以下要求：
        1) 小蓝不喜欢数字 0 ，所以数字字符串中不可以出现 0 ；
        2) 小蓝喜欢数字 3 和 7 ，所以数字字符串中必须要有 3 和 7 这两个数字。
请问满足题意的数字字符串有多少个？这个数字会很大，你只需要输出其
对 10 9 + 7 取余后的结果。

分析：

每个位置9种情况
一共9^10000种
没有3的有8^10000种
没有7的也有8^10000种
这两个多算了一份没有3和7的
最后加上一份同时没有3和7的
7^10000种
 

def ksm(a, b, mod):
    if b == 0:
        return 1
    t = ksm(a, b // 2, mod)
    t = (t * t) % mod
    if b & 1:
        t = (t * a) % mod
    return t % mod
##快速幂板子

mod = 10**9 + 7
ans = ksm(9, 10000, mod) - 2 * ksm(8, 10000, mod) + ksm(7, 10000, mod)
ans %= mod
print(ans)

8.迷宫问题

#maze表示迷宫
maze=[
[0,1,0,0,0],
[0,1,1,1,0],
[0,0,0,0,0],
[0,0,0,0,0],
[0,1,1,1,0]
]

#表示向四个方向移动坐标
dirs=[
	lambda x,y:(x+1,y),
	lambda x,y:(x-1,y),
	lambda x,y:(x,y+1),
	lambda x,y:(x,y-1)
]

def stack_path(x1,y1,x2,y2):
	#x1,y1:初始坐标；x2,y2:表示终点坐标
	stack=[]              #建一个空列表，当做一个栈
	stack.append((x1,y1))     #将初始坐标存起来
	while(len(stack)>0):      #栈内有元素就循环
		curNode=stack[-1]     #取当前坐标
		if curNode[0]==x2 and curNode[1]==y2:                #当前坐标等于终点坐标，路径找到，结束程序
			for p in stack:
				print("(%d,%d)" % (p[0],p[1]))
			return True

		for dir in dirs:                                #遍历四个方向
			nexNode=dir(curNode[0],curNode[1])
			if 0<= nexNode[0]<=x2 and 0<= nexNode[1]<= y2:           #坐标没有越界
				if maze[nexNode[0]][nexNode[1]] == 0:       
					stack.append(nexNode)                      #坐标等于0，就把他放入栈中，并标记为2
					maze[nexNode[0]][nexNode[1]] = 2
					break
			else:                            #坐标越界了，进入下轮循环，看其他方向
				continue
		else:                             #如果没有路可以走，回退，将当前节点出栈,如果for循环正常结束，else中语句执行。如果是break的，则不执行。
			stack.pop()
	else:
		return False
	
stack_path(0,0,4,4)

9.包子问题（DP）

import os
import sys

import math
N = 10000
dp = [0 for i in range(N)]
n = int(input())  # n 为第几个笼子
a = [int(input()) for j in range(n)]  # 循环输入每个笼子中的小笼包数量
g = a[0]
for i in range(n):
    g = math.gcd(g,a[i])  # 求得笼子中的小笼包数量的最大公约数，若不为1，则说明其肯定有一种组合是无法表示的，固有无限可能，需要输出INF
if g == 1:  #  使用完全背包算法求解不能表示的数
    dp[0] = 1  # 将第一个数标记为1
    for i in range(n):  # 有几种笼子的类型就遍历几种
        for j in range(a[i],N):  # a[i]对应的是笼子中的小笼包数量
            dp[j] = max(dp[j],dp[j-a[i]])  # 状态转移方程式，j-a[i]相当于反向从10000开始递减单个笼子的数量，从而达到单个倍数的可能性，并给可以取到的数标记为1
            # 对于组合数，比如3，4，5、7咱们又是如何取得到的呢？ dp[7]=0,但是dp[7-a[i]]=dp[7-4]=dp[3]=1,也就是说这个数可以被第一个数和第二个数相加得到，因此也可以被标记
    print(N-sum(dp))
else:
    print('INF')

10.管道（差分+二分）

'''
覆盖问题，二分
'''
from sys import stdin

def check(x) :
    st = [0] * (m + 2)
    for item in a :
        if item[1] <= x :
            l, r = max(item[0] - (x - item[1]), 1), min(item[0] + (x - item[1]), m)
            st[l] += 1
            st[r + 1] -= 1
    for i in range(1, m + 1) :
        st[i] += st[i - 1]
        if st[i] <= 0 :
            return False
    return True
                

n, m = map(int, input().split())

a = []

for _ in range(n) :
    l, s = map(int, stdin.readline().split())
    a.append([l, s])

l, r = 0, m + 1
while l < r :
    mid = (l + r) >> 1
    if check(mid) :
        r = mid
    else :
        l = mid + 1
print(l)

11.背包问题

1.01背包

#dp[i][j]    前i件物品，总体积不超过j 的最大价值

n,v=map(int,input().split())
dp=[[0]*(v+1) for i in range(n+1)]

for i in range(1,n+1):
    wi,vi=map(int,input().split())
    for j in range(0,v+1):
        if j>=wi:
            dp[i][j]=max(dp[i-1][j],dp[i-1][j-wi]+vi)
        else:
            dp[i][j]=dp[i-1][j]
            
print(dp[n][v])

2.完全背包

import os
import sys
N, V = map(int, input().split())
items = []
for _ in range(N):
    w, v = map(int, input().split())
    items.append((w, v))
dp = [0] * (V + 1)
for i in range(1, V + 1):
    for w, v in items:
        if i >= w:
            dp[i] = max(dp[i], dp[i - w] + v)
print(dp[V])
'''
读取输入的商场物品数量N和小明的背包容量V，以及每种物品的体积和价值。
初始化一个长度为V+1的动态规划数组dp，dp[i]表示背包容量为i时所能获得的最大价值。
使用动态规划求解，外层循环遍历背包容量从1到V，内层循环遍历每种物品，更新dp[i]的值为dp[i-w]+v和当前dp[i]的较大值。
输出dp[V]即为小明所能获得的最大价值。
'''

3.多重背包

#dp[i][j] =max(dp[i][j],dp[i-1][j-k*wi]+k*vi)  k属于(0，si)

n,v=map(int,input().split())
dp=[[0]*(v+1) for i in range(n+1)]
for i in range(1,n+1):
    wi,vi,si=map(int,input().split())
    for j in range(0,v+1):
        for k in range(0,min(si,j//wi)+1):

            dp[i][j]=max(dp[i][j],dp[i-1][j-k*wi]+k*vi)

print(dp[n][v])

4.混合背包

import os
import sys

# 请在此输入您的代码
N, V = map(int, input().split())
dp = [0]*(V+1)
for _ in range(N):
  w, v ,n= map(int, input().split())
  #如果n为0或者n*w大于等于V，说明该物品只能选择一次或者不能选择，因此直接使用01背包的方式更新dp列表
  if n==0 or n*w>=V:
    for j in range(w,V+1):
      dp[j] = max(dp[j], dp[j-w]+v)
  #否则，对于每个物品，使用完全背包的方式更新dp列表。
  elif n>0:
    for k in range(n):
      for j in range(V,w-1,-1):
        dp[j] = max(dp[j], dp[j-w]+v)
print(dp[-1])

12.分糖果（暴力dfs）

import os
import sys

ans=0

#n,m为剩余糖果数量
def dfs(death,n,m):
  if death==7:
    if n==0 and m==0:
      global ans
      ans+=1
    return

  for i in range(0,6):
    for j in range(0,6):
      if 2<=i+j<=5 and i<=n and j<=m:
        dfs(death+1,n-i,m-j)
dfs(0,9,16)
print(ans)

13.N皇后问题（dfs）

n=int(input())
vis1=[0]*(n+1)
vis2=[0]*(2*n+2)
vis3=[0]*(2*n+2)
ans=0

def dfs(x):
    global ans
    if x>n:
        ans+=1
        return
    for i in range(1,n+1):
        if vis1[i]==0 and vis2[x+i]==0 and vis3[x-i+n]==0:
            vis1[i]=vis2[x+i]=vis3[x-i+n]=1
            dfs(x+1)
            vis1[i]=vis2[x+i]=vis3[x-i+n]=0
dfs(1)
print(ans)

14.datetime库

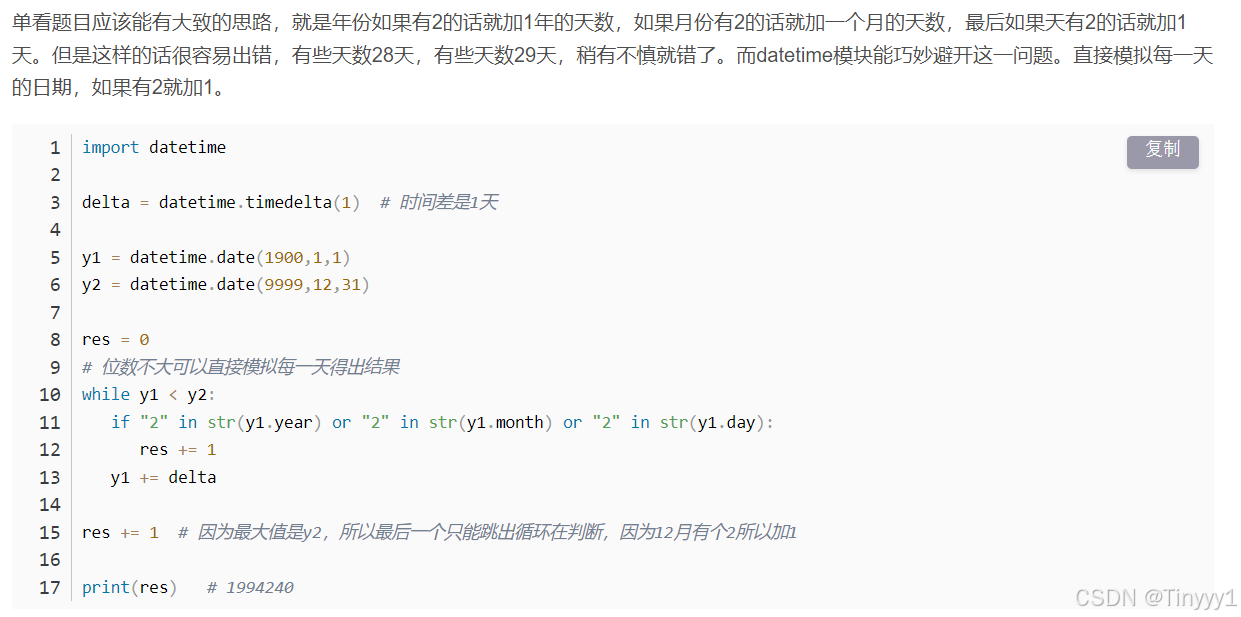
15.挖矿

import os
import sys

n,m=map(int,input().split())
a=list(map(int,input().split()))

r=[0]*(m+1)
l=[0]*(m+1)

for i in a:
  if i>0 and i<=m:
    r[i]+=1
  if i<0 and abs(i)<=m:
    l[abs(i)]+=1

for i in range(m+1):
  r[i]+=r[i-1]
  l[i]+=l[i-1]

ans=0
for i in range(1,m//2+1):
  ans=max(ans,r[i]+l[m-2*i],l[i]+r[m-2*i])
ans=max(ans,l[m],r[m])


if 0 in a:
  ans+=1

print(ans)