SORT中的卡尔曼滤波学习笔记k

最新推荐文章于 2025-08-17 17:03:36 发布

原创最新推荐文章于 2025-08-17 17:03:36 发布 · 941 阅读

21 ·

CC 4.0 BY-SA版权

文章标签：

#学习 #笔记

参考文献：

【论文解读】Simple Online and Realtime Tracking - 知乎

How a Kalman filter works, in pictures | Bzarg

多目标跟踪算法——SORT - 渐渐的笔记本 - 博客园

Kalman Filter

使用场景：对某个动态系统有不确定信息的地方使用卡尔曼滤波器，并且可以对系统下一步要做什么做出有根据的预测。

预测

卡尔曼滤波器需要对系统的状态进行建模（类似于自控里的状态空间方程），如一个在某个空间中的机器人，如果我们需要关注的是它的位姿，那么对其进行建模的结果就可以是：

$X=\begin{bmatrix} p\\ v \end{bmatrix}$

卡尔曼滤波器假设这两个个变量是随机且满足高斯分布的，那么每一个变量都应有一个平均值 $\mu$ 和一个方差 $\sigma ^2$ ，而变量之间存在一定的相关性，如位置p会根据机器人的速度和角度发生变化，这样的相关性将通过协方差矩阵进行描述，即：

$P_k=\begin{bmatrix} \Sigma_{pp}& \Sigma_{pv}\\ \Sigma_{vp}& \Sigma_{vv} \end{bmatrix}$

卡尔曼滤波器的最终目的是预测，即是需要从k-1时刻的状态预测k时刻的状态，在这里我们可以根据系统的物理模型（假设机器人做匀速直线运动，即运动方程为线性）写出一个转移矩阵（和状态空间方程十分类似），即：

$p_{k} = p_{k-1} + v_{k-1} \cdot \Delta t \\ v_{k} = \qquad \quad v_{k-1}$

所以系统的运动方程可以表示为：

$\hat{X}_{k|k-1} = \begin{bmatrix} 1 & \Delta t \\ 0 & 1 \end{bmatrix} \hat{X}_{k-1|k-1} \\ = F_k\hat{X}_{k-1|k-1}$

同时协方差矩阵的更新方程为：

$P_{k|k-1} = F_k P_{k-1|k-1} F^{T}_{k}$

上述过程的一个很强的假设是系统做匀速直线运动，但实际上系统会存在外部输入使系统做非匀速直线运动，如匀加速，此时在建立系统的运动方程时需要加入外部影响：控制矩阵 $B_k$ 和控制向量 $\vec{u_k}$ ：

$p_k = p_{k-1} + \Delta t v_{k-1} + \frac{1}{2} a \Delta t^2 \\ v_k = \quad \quad \quad \quad v_{k-1} + a \Delta t$

进一步地，写为矩阵形式：

$\hat{X}_{k|k-1} = F_k \hat{X}_{k-1|k-1} + \begin{bmatrix} \frac{\Delta t^2}{2}\\ \Delta t \end{bmatrix}a \\ = F_k \hat{X}_{k-1|k-1} + B_k \vec{u_k}$

现在为止，算是把更新的过程建立完成了，但实际上，KF的本质是从未知和不确定中进行预测，不确定的来源很多，其中一个便是模型的不确定性，所以对上述过程进行进一步完善，我们选择在每一步预测中对系统状态加入一定的不确定性（满足高斯分布的噪声的协方差矩阵 $Q_k$ ），可以参考下图理解转移方程预测状态中不确定性的影响。

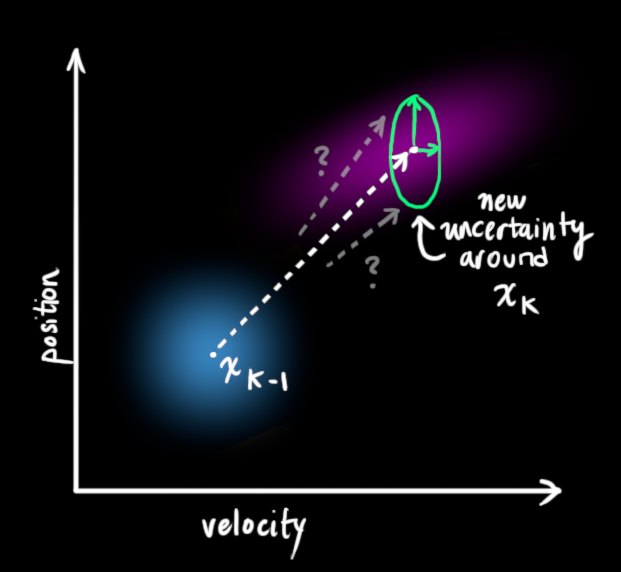
所以系统状态的协方差矩阵预测方程变为：

$P_k = F_k P_{k-1} F^{T}_{K}+Q_k$

所以，现在可以将KF的预测过程总结为：最新的系统状态预测为根据过去的最佳估计加上已知外部影响的矫正；最新的系统状态协方差预测为过往的协方差矩阵加上来自环境的不确定性。

更新

好了，在上一部分中已经明确了预测的过程，里面提到了过去的最佳估计，这个最佳又从何谈起呢，这个时候如果我们引入一个传感器，它能够观测到系统变量（注意：是观测而非测量，也就是说传感器不一定能直接测量出我们定义的系统变量，但是可以通过测量出的量推算出系统变量，就像IMU虽然不能直接测量运动速度，但是可以对加速度做积分得到运动速度一样。），那么这时候就可以将观测量也加入进来，考虑到测量所得不一定为系统变量，所以还需根据物理模型提出一个观测矩阵在观测量和系统变量之间相互转换：（协方差矩阵使用 $R_k$ 来表示）

$Z_k = H_k \hat{X}_k + u_k$

在这里，我们再回顾一下KF是在干什么，我们希望根据过去的系统状态推测现在的系统状态，首先我们想尝试用系统的过程矩阵描述，ok，很成功，然后我们发现还有传感器可能能够直接测量得到现在的系统状态，但两者都存在一定的不确定性（使用协方差矩阵来表示），现在我们理所当然的就想用这两条路径的推测结果相互佐证，来得到最佳估计，没错，这就是KF的工作本质。有一组图我认为很好的诠释了更新过程所做的事情，里面粉色代表第一条路径，绿色代表第二条路经。

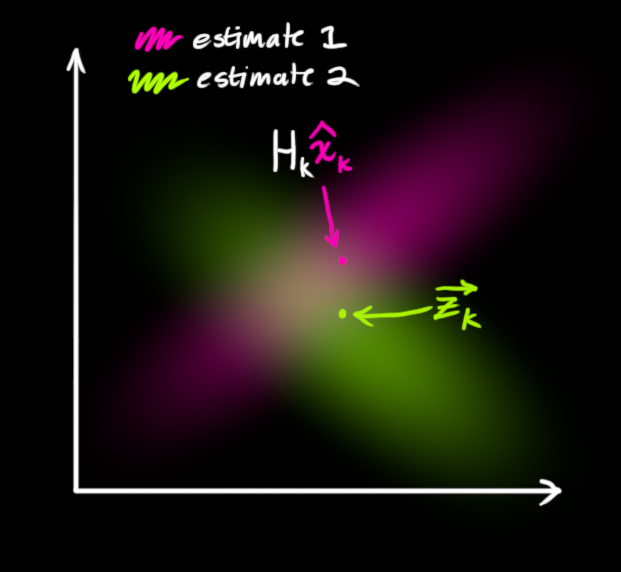
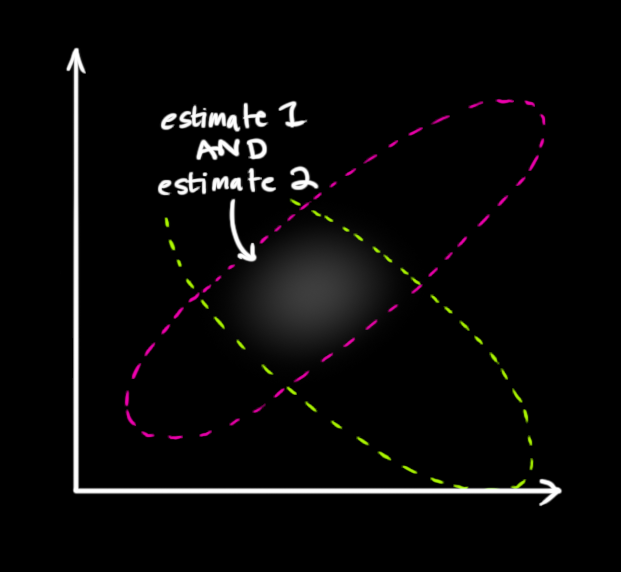
卡尔曼增益

如果你之前了解过KF，那你肯定知道在卡尔曼滤波的过程中有个核心参数叫做卡尔曼增益，关于它的来源和计算公式的推导可以参考下面的文章。（由于笔者的数学能力实在太差，我也不能完全理解并进行解释，希望大家能够有所收获。）

卡尔曼滤波最完整公式推导 - 知乎

卡尔曼滤波算法详细推导（全网最详细的推导过程）_卡尔曼滤波推导-优快云博客

我们最终需要的结论即是卡尔曼增益的计算公式：

$K = P_{k|k-1} H^{T}_k (H_k P_{k|k-1} H^{T}_k+R_k)^{-1}$

更新流程

现在我们掌握的信息包括根据上一时刻系统状态做出的估计 $\hat{X}_{k|k-1}$ 和当前时刻的观测结果 $Z_k$ ，我们希望能够融合这两类信息，让它们带者各自的权重参与到对当前时刻系统状态的预测中，而权重的分配我们将其交给卡尔曼增益完成。

$\hat{X}_{k|k} = \hat{X}_{k|k-1} + K(Z_k - H_k\hat{X}_{k|k-1})\\ P_{k|k} = P_{k|k-1} - KH_kP_{k|k-1}$

整个卡尔曼滤波的流程画成框图表示：

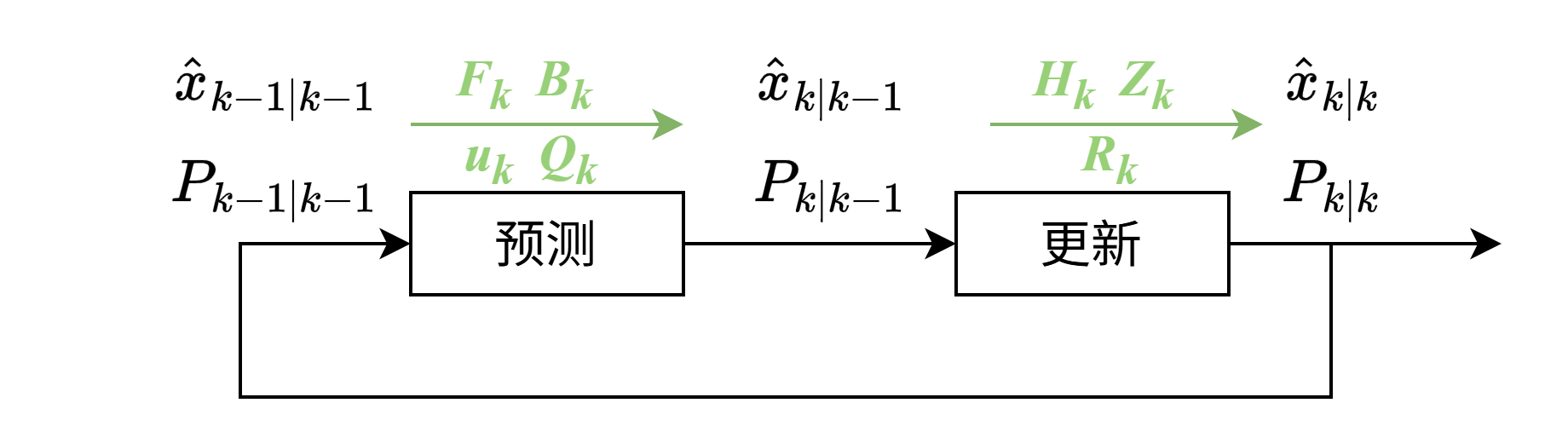
（以上内容均翻译自How a Kalman filter works, in pictures | Bzarg，框图为笔者亲自绘制，如果使用请注明来源）

在SORT中KF的作用

其实看一下SORT算法的流程图我们就能够大致明白KF在其中是如何工作的：

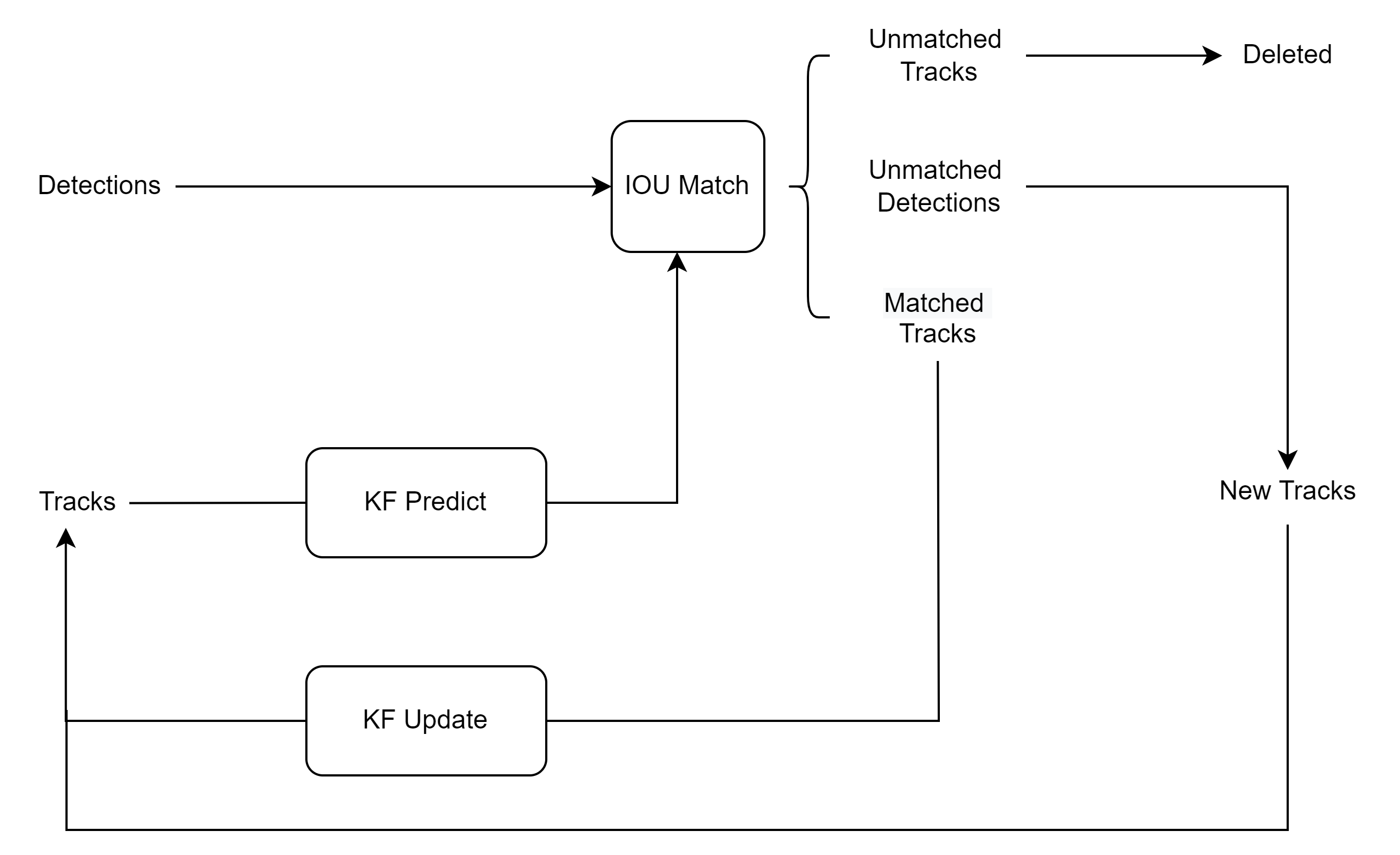
图片来源：目标跟踪——SORT算法原理浅析-优快云博客

SORT是一种典型的Tracking By Detecion框架，检测网络从每一帧视频中输出每个目标的Bounding Box，跟踪算法中将对每一个目标都创建一个KF，对下一帧中检测框的位置、大小进行预测，在下一帧中检测网络继续输出BBox，那么此时就有了预测的BBox和观测的BBox，仅依靠检测网络和KF并不能确定这两个BBox的对应关系，所以SORT又使用了IoU和匈牙利算法，使每个目标的BBox能够获得正确的对应关系（非本文重点，故不展开），而观测的BBox又可以用于KF的更新过程，继而得到新的预测BBox，参考下图。

图片来源：多目标追踪 SORT 算法：Simple Online and Realtime Tracking | 四一的随写

下面分别分析SORT中使用KF进行预测和更新的过程：

预测

和前文中所讲到卡尔曼滤波的应用场景不同，在SORT中KF不再用于预测一个空间中物体的运动，而是被用来预测下一帧中BBox的位置，所以状态量应选择和BBox相关的参数，转移矩阵的建立也应做出相应的改动，在SORT中，作者将状态量和转移矩阵设置为了：

$X = [u,v,s,r,\dot{u},\dot{v},\dot{s}] \\ u_k = u_{k-1} +\dot{u} \times 1 \\ v_k = v_{k-1} + \dot{v} \times 1 \\ s_k = s_{k-1} + \dot{s} \times 1 \\ r_k = r_{k-1} \\ \dot{u} = \dot{u} \quad ...\\ F_k = \begin{bmatrix} 1 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{bmatrix}$

其中 $(u,v)$ 表示BBox的中心点坐标，s为BBox的面积，r为BBox的长宽比，这四个变量将根据第一帧的观测结果进行初始化， $\dot{u}, \dot{v}, \dot{s}$ 分别表示对应变量的变化率，初始值为0，后续将根据预测结果进行变化。而协方差矩阵 $P_k$ 则将根据变量关系自行设计。

更新

从框图中即可知晓，所谓更新过程即是在建立KF预测的BBox与Detection输出的BBox之间的对应关系之后，利用观测（Detection）进一步修正预测的BBox位置，然后输出给下一帧使用，所以这里将观测定义为了在每一个Track对应的Detection输出BBox的对应参数：

$Z = [u, v, s, r] \\ Z = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 \end{bmatrix}X$

剩下的内容就和普通的KF一样了，计算卡尔曼增益，更新X到下一帧。

思考

在SORT里作者将BBox在每帧之间的变化过程定为了线性变化（参考 $F_k$ ），但实际上当相机在移动，也就是画布也在发生相对运动的时候，并不将BBox的运动简化为线性模型，所以笔者在考虑当相机和背景也存在相对运动，即运动中的相机跟踪运动中的目标，这样的情境下对运动方程进行改写，建立一个更切合实际的非线性方程，然后使用EKF/UKF/AKF完成每一帧中目标的跟踪。