我是Tina表姐,毕业于中国人民大学,对数学建模的热爱让我在这一领域深耕多年。我的建模思路已经帮助了百余位学习者和参赛者在数学建模的道路上取得了显著的进步和成就。现在,我将这份宝贵的经验和知识凝练成一份全面的解题思路与代码论文集合,专为本次赛题设计,旨在帮助您深入理解数学建模的每一个环节。
本次美赛(6题)完整内容均可以在文章末尾领取!(部分代码在本帖子里格式混乱,下载后格式正常)
本次美赛D题可以做如下考虑
在这个问题中,关于巴尔的摩的交通网络模型构建,可以从以下几个方面入手:
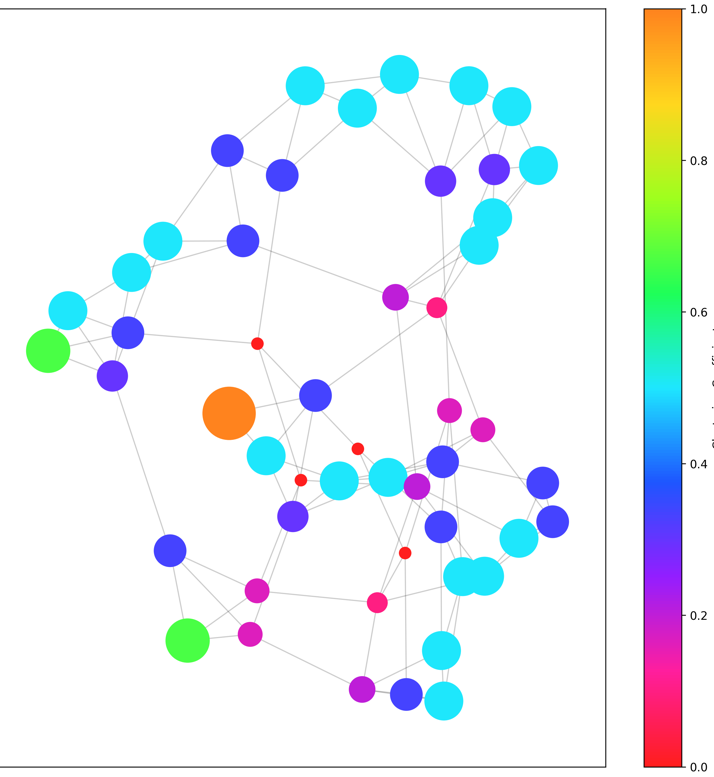
添加图片注释,不超过 140 字(可选)
-
数据整理与处理:
-
收集和整理提供的数据集,如 Bus_Routes.csv、Bus_Stops.csv、edges_drive.csv 等,确保数据格式一致,去除重复项和错误数据。
-
汇总交通流量数据 MDOT_SHA_Annual_Average_Daily_Traffic_Baltimore.csv,为不同路段和街道段的交通量做分析。
-
交通网络建模:
-
根据 nodes_all.csv 和 edges_all.csv 创建一个图形模型,其中节点代表交通枢纽、路口或公交站,边代表道路或交通路径。
-
使用网络分析工具(如 Python 中的 NetworkX 库)来计算交通流、车流密度和潜在的瓶颈位置。
-
影响分析:
-
评估弗朗西斯·斯科特·基伊桥的坍塌对周边交通的影响,开展交通流量分析,识别出受影响最严重的路段和公共交通路线。
-
可以利用仿真工具(如 AnyLogic 或 VISSIM)模拟不同场景下的交通情况,以了解重建桥梁的必要性和影响。
-
利益相关者分析:
-
确定不同利益相关者(居民、通勤者、商家等)在交通网络中的角色,分析他们的需求和优先级,例如公共交通改善的需求,步行道和骑行道的安全性等。
-
通过可视化工具(如 GIS 软件)展示不同利益相关者的地理分布及其对交通方案的反馈。
-
项目建议及影响评估:
-
推荐一个能够显著改善居民生活的交通项目,比如改善某个公交线路或步行道系统,具体描述该项目的实施步骤和预期效果。
-
评估项目对其他利益相关者(如通勤者、企业主、游客)的影响,说明如何在满足特定利益相关者需求的同时,平衡其他利益相关者的需求。
-
解决方案和备忘录撰写:
-
撰写完整的解决方案文档,包含摘要、目录、各部分详细分析、推荐项目及其效益及影响。
-
为巴尔的摩市市长撰写备忘录,概述所提出的两个项目及其对城市人们生活和安全的影响,包括潜在的风险和解决方案。
在这一过程中,确保所使用的数据和模型能够真实反映巴尔的摩市的交通状况,以便为利益相关者提供可靠的决策支持。 为了对巴尔的摩市弗朗西斯·斯科特·基伊桥的坍塌影响进行建模,我们可以按照以下步骤进行分析与建模:
1. 交通网络建模
我们首先可以构建一个图形模型来表示巴尔的摩的交通网络。我们将网络中的节点(vertices)表示为交通枢纽、路口或公交站,边(edges)表示道路或交通路径。使用提供的数据文件 nodes_all.csv 和 edges_all.csv 替我们提供了节点及其连接关系。
网络模型的构建
-
节点表示:每个节点 $v_i$ 代表一个地理位置或交通交叉点。
-
边表示:每条边 $e_{ij}$ 连接节点 $v_i$ 和 $v_j$,代表这两个地点之间的交通路径。边的权重可以使用交通流量数据(例如:从 MDOT_SHA_Annual_Average_Daily_Traffic_Baltimore.csv 中获得)来表示。
2. 交通流量分析
在桥梁坍塌之后,交通流量可能会明显变化。我们可以设想一个简单的交通流量模型来描述这一变化,基于流量守恒原理。设某一条道路的流量为 $Q_{ij}$,我们可以使用以下公式来表示:
其中: - $C_{ij}$ 是道路的能力(capacity),可以通过道路类型和宽度等因素来确定。 - $D_{ij}$ 是交通需求,表示从起点到终点的流量需求。 - $\gamma_{ij}$ 是路段的延迟或其他影响因素,比如桥梁的关闭导致的流量改变。
3. 桥梁影响的范围分析
我们需要测量桥梁坍塌对周边交通流量的全局影响。可以利用加权图的连通性来评估。从坍塌点出发,我们可以寻找与这个点最相关的所有节点(即使用广度优先搜索或深度优先搜索算法),评估影响范围。
定义一个影响范围的函数:
其中 $N(v_k)$ 是与节点 $v_k$ 相邻的所有节点,$Q_{kj}$ 是影响节点 $v_j$ 的流量。
4. 利益相关者分析
我们需要识别出受到影响的不同利益相关者,包括: - 居民:通勤时间增加,出行不便。 - 通勤者:需要寻找新的路线或替代交通工具。 - 商家:运输成本增加,顾客流失。 - 游客:可能影响他们到达旅游景点的可达性。
为每个利益相关者定义相应的损失函数,例如通勤者的损失可以表示为:
其中 $T_{new}$ 和 $T_{old}$ 分别为新的和旧的通勤时间。
5. 仿真与优化
我们可以使用仿真工具(如 AnyLogic、VISSIM 等)来模拟不同场景,测试重建桥梁的优先策略及其对降低影响的效果。同时,通过优化算法(如线性规划或遗传算法)来寻找最佳的交通流重定向方案,以降低影响。
结论
通过以上步骤,我们可以创建一个有效的交通网络模型,分析弗朗西斯·斯科特·基伊桥的坍塌对巴尔的摩交通系统的影响。通过验证交通流模型和利益相关者的分析,我们能够为政策制定者提供科学依据,为重建桥梁和改善交通网络的决策奠定基础。 非常感谢您的提问!以下是关于如何构建一个交通网络模型来研究巴尔的摩的交通问题的思路,聚焦于数据整理、网络建模和影响分析。
1. 数据整理与处理
在创建模型之前,必须对收集到的数据进行妥善整理与处理。可以按照如下步骤进行:
-
数据匹配和清理:将 Bus_Routes.csv、Bus_Stops.csv 和 edges_drive.csv 数据集中关于公交线路和街道的信息进行比对与清理,确保没有重复和错误的数据。
-
地理信息整合:利用 nodes_all.csv 和 edges_all.csv 中的信息,将公交站点与道路网络相连接,使其成为一个综合的交通模型。
2. 交通网络建模
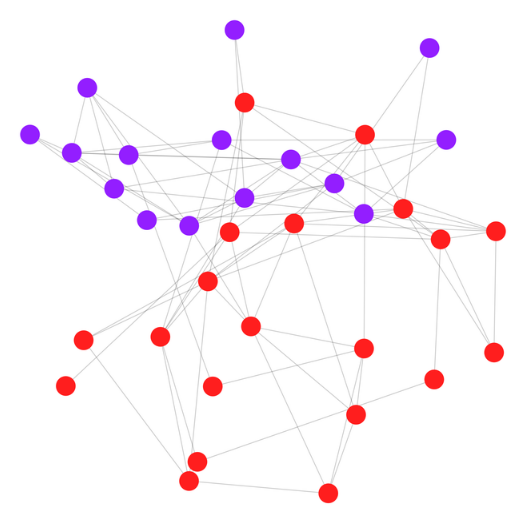
添加图片注释,不超过 140 字(可选)
在构建交通网络模型时,可以运用图论的概念:
-
定义节点和边:
-
节点代表交通枢纽(如公交站、交叉路口)。
-
边代表道路或交通路径的连接。例如使用 edges_drive.csv 中的路段连接公交线路和步行道。
-
构建图形模型:可以使用如下形式构建图形:
-
设 $G = (V, E)$,其中 $V$ 是节点集合,$E$ 是边集合。
-
计算流量和通行能力:通过分析 MDOT_SHA_Annual_Average_Daily_Traffic_Baltimore.csv 中的数据,可以得到每个路段的车辆流量 $A_{ij}$,其中$i, j$表示相邻的节点。可以用以下公式计算:
3. 影响分析
在评估弗朗西斯·斯科特·基伊桥坍塌后的影响时,考虑以下方面:
-
交通流量变化:通过在模型中删除该桥的边,重新计算交通流量,观察交通流的变化。
-
设计影响可视化:利用流量和速度数据,创建影响图,突出显示交通瓶颈和被影响的主要交通路线。
-
利益相关者影响:
-
居民(公交依赖者)在此情况下可能会面临更长的通勤时间。
-
商家可能因接入不便而损失客户。
独特见解
在交通网络的模型设计中,强调多模式交通(公交、步行、自行车等)是非常重要的。通过简化和优化不同模式之间的连接,能够促进更高效的出行方式,满足各类群体的需求。例如,通过增加公交站点的可及性和步行道系统的连通性,可以大大提高城市居民日常出行的便利性。这种交通模型并非只是关注车辆流,而是在于优化整体交通生态,使每一种交通模式协同工作,服务于多样化的利益相关者。
通过以上步骤,有助于深入理解巴尔的摩的交通问题和改善方案,为实现更可持续的城市交通体系提供基础数据支撑。 要构建巴尔的摩的交通网络模型,首先需要集中在数据整理、处理和建模的关键步骤。我们将讨论如何实现这一过程,并展示需要用到的数学工具和公式,特别是在交通流和网络分析方面。
1. 数据整理与处理
我们需要从提供的数据集中提取并整理数据,以构建可靠的交通网络模型。
数据清洗
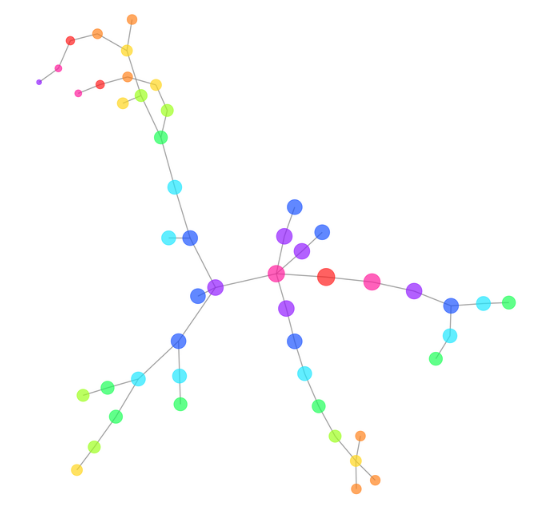
添加图片注释,不超过 140 字(可选)
-
去重与一致性: 检查所有数据集中的重复项,确保每个公交线路、路段和交通节点信息都是唯一且准确的。例如,使用 Python 的 Pandas 库进行数据清洗:
```python import pandas as pd
bus_routes = pd.read_csv("Bus_Routes.csv").drop_duplicates() bus_stops = pd.read_csv("Bus_Stops.csv").drop_duplicates() ```
-
缺失值处理:处理缺失值可能使用填补或删除的方法,具体取决于数据的性质。
2. 交通网络建模
交通网络可以用图形理论来表示,其中节点表示交通交叉口、公交站等,而边则表示道路或交通路线。我们可以定义以下变量:
-
节点集 $V$:所有的节点,例如 $V = {v_1, v_2, \ldots, v_n}$。
-
边集 $E$:所有的





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 2054
2054

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








