常见数据结构-TrieTree/线段树/TreeSet

线段树

  线段树是一种非常灵活的数据结构，它可以用于解决多种范围查询问题，比如在对数时间内从数组中找到最小值、最大值、总和、最大公约数、最小公倍数等。

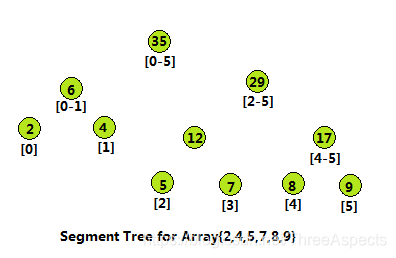
数组A[0,1,…,n−1 ] 的线段树是一个二叉树，其中每个节点都包含数组的一个子范围[i…j] 上的聚合信息（最小值、最大值、总和等），其左、右子节点分别包含范围[i,（i+j）/2] 和[（i+j）/2+1,j] 上的信息。
  线段树既可以用数组也可以用树来实现。对于数组实现，如果索引 ii 处的元素不是一个叶节点，那么其左子节点和右子节点分别存储在索引为2i和2i+1 的元素处。在上图所给出的示例中，每个叶节点都包含初始的数组元素 {2,4,5,7,8,9}。内部节点包含范围内相应元素的总和11是从索引 0 到索引 2 的元素之和。而根节点 (35) 是它的两个子节点 (6) 和 (29) 的和,也是整个数组的和。
线段树可以分为以下三个步骤：
【1】从给定数组构建线段树的预处理步骤。
【2】修改元素时更新线段树。
【3】使用线段树进行区域和检索。

【构建线段树】
  这里使用一种非常有效的自下而上的方法来构建线段树。从上图示可知，如果某个节点 p包含范围[i…j] 的和，那么其左、右子节点分别包含范围[i,（i+j）/2] 和[（i+j）/2+1,j] 上的和。因此，想要找到节点 p 的和，需要提前计算其左、右子节点的和。从叶节点开始，用输入数组的元素a[0,1,…,n−1] 初始化它们。然后逐步向上移动到更高一层来计算父节点的和，直到最后到达线段树的根节点。

int[] tree;
int n;
public NumArray(int[] nums) {
    if (nums.length > 0) {
        n = nums.length;
        tree = new int[n * 2];
        buildTree(nums);
    }
}
private void buildTree(int[] nums) {
    for (int i = n, j = 0;  i < 2 * n; i++,  j++)
        tree[i] = nums[j];
    for (int i = n - 1; i > 0; --i)
        tree[i] = tree[i * 2] + tree[i * 2 + 1];
}

【更新线段树】
  当更新数组中某个索引i处的元素时，需要重建线段树，因为一些树节点上的和值也会随之产生变化。将再次使用自下而上的方法。首先更新存储a[i] 元素的叶节点。从那里将一路向上，直到根节点，并用其子节点值的总和来更新每个父节点的值。

void update(int pos, int val) {
    pos += n;
    tree[pos] = val;
    while (pos > 0) {
        int left = pos;
        int right = pos;
        if (pos % 2 == 0) {
            right = pos + 1;
        } else {
            left = pos - 1;
        }
        // parent is updated after child is updated
        tree[pos / 2] = tree[left] + tree[right];
        pos /= 2;
    }
}

【区域和检索】
  通过以下方式使用线段树进行区域和检索 [L,R]：算法保持循环不变，l≤r 以及已经算出[L…l] 和 [r…R] 的总和，其中l 和r 分别是计算总和时的左边界和右边界。每次迭代的范围 [l,r]都会缩小，直到在算法的大约 log n次迭代后两个边界相遇为止。

public int sumRange(int l, int r) {
    // get leaf with value 'l'
    l += n;
    // get leaf with value 'r'
    r += n;
    int sum = 0;
    while (l <= r) {
        if ((l % 2) == 1) {
           sum += tree[l];
           l++;
        }
        if ((r % 2) == 0) {
           sum += tree[r];
           r--;
        }
        l /= 2;
        r /= 2;
    }
    return sum;
}

TreeSet

  TreeSet是一个有序的集合，它的作用是提供有序的Set集合。它继承了AbstractSet抽象类，实现了NavigableSet< E >，Cloneable，Serializable接口。TreeSet是基于TreeMap实现的，TreeSet的元素支持2种排序方式：自然排序或者根据提供的Comparator进行排序。

TreeSet常用方法：

public boolean add（E e）
如果指定的元素尚不存在，则将其添加到此集合中。更正式地说，e如果集合中不包含任何元素，则将指定的元素添加到此集合e2中 Objects.equals(e, e2)。如果此set已包含该元素，则调用将保持set不变并返回false。

public boolean isEmpty（）
true如果此set不包含任何元素，则返回

public E ceiling​(E e)
返回此set中大于或等于给定元素的最小元素，或者null如果没有这样的元素。

public E floor(E e)
返回此set中小于或等于给定元素的最大元素，或者null如果没有这样的元素。

public E lower​(E e)
返回此集合中的最大元素严格小于给定元素，或者null如果没有这样的元素。

public boolean contains（Object o）
true如果此set包含指定的元素，则返回。更正式地说，返回true当且仅当此set包含的元素e，使得 Objects.equals(o, e)。

TrieTree

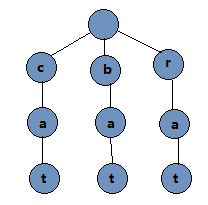
  一个线性表的顺序查找的时间复杂度为O(n)，二分搜索树的查找为O(log n)，均与数据结构中的元素个数相关。Trie字典树(主要用于存储字符串)查找速度主要和它的元素(字符串)的长度相关[O(w)]。Trie字典树主要用于存储字符串，Trie 的每个 Node 保存一个字符。用链表来描述的话，就是一个字符串就是一个链表。每个Node都保存了它的所有子节点。例如我们往字典树中插入"cat", “bat”, "rat"三个单词，Trie字典树如下所示：

class Solution {
    public String replaceWords(List<String> dict, String sentence) {
        Trie trie=new Trie();
        String[] sentences=sentence.split(" ");
        for(String s:dict){
            trie.add(s);
        }
        StringBuffer sb=new StringBuffer();
        for(String s:sentences){
            sb.append(func(s,trie));
            sb.append(" ");
        }
        return sb.substring(0,sb.length()-1);
    }
    public String func(String s,Trie trie){
        StringBuffer sb=new StringBuffer();
        Node cur = trie.root;
        for(int i=0;i<s.length();i++){
            sb.append(s.charAt(i));
            if(cur.map.containsKey(s.charAt(i))){
                cur=cur.map.get(s.charAt(i));
                if(cur.isWord) return sb.toString();
            }else{
                return s;
            }
        }
        return s;
    }
}
class Node{
    boolean isWord;
    Map<Character,Node> map;
    public Node(){
        isWord=false;
        map=new HashMap<>();
    }
}
class Trie{
    Node root;
    public Trie(){
        root=new Node();
    }
    public void add(String str){
        Node cur=root;
        for(int i=0;i<str.length();i++){
            if(!cur.map.containsKey(str.charAt(i))){
                cur.map.put(str.charAt(i),new Node());
            }
            cur=cur.map.get(str.charAt(i));
        }
        cur.isWord=true;
    }
    public boolean contains(String str){
        Node cur=root;
        for(int i=0;i<str.length();i++){
            if(cur.map.containsKey(str.charAt(i))){
                cur=cur.map.get(str.charAt(i));
            }else{
                return false;
            }
        }
        return cur.isWord;
    }
}