数据结构-链表

链表

什么是链表

链表和数组一样是一种非常基础和常见的数据结构，其特点是可以利用指针，将内存中不连续的内存块串联起来使用，不需要像数组一样去预分配内存和容量，并且在某些情况下删除和添加性能比数组要快。最基础的链表形式为单向链表，其数据存储单元称为节点，每个节点除了存放数据之外，还维护着一个指针，指向下一个节点。除了单向链表，还有一些更复杂的形式，如双向链表、循环链表等。

链表种类

单向链表

单向链表的结构如下图，其特点是每个节点都有一个指针指向下一个节点

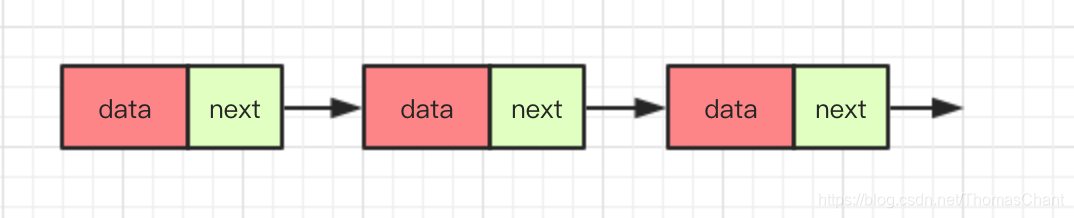
单向链表的查找时间复杂度为O(n),往链表中添加或删除节点需要看具体情况，如果被删除节点是在头部，则复杂度为O(1)，在其他位置则平均复杂度为O(n),因为要先找到对应的节点再进行操作。

双向链表

双向链表和单向链表不同之处在于每个节点多了一个指针，用于指向前节点，虽然增加空间上的开销，但是相比单向节点在某些情况下具有了更高的性能，比如删除某个已知节点的前节点，对于单链表需要先遍历找到对应的前节点再进行删除，此时时间复杂度为O(n)，但是双向链表就不需要额外的查找操作，时间复杂度为O(1)。其结构如下图：

单向循环链表

单向循环列表的特点是尾节点是指向首节点的，和单链表相比，从链尾到链头比较方便，在处理一些需要环形结构的问题时就比较方便，比如著名的约瑟夫问题。

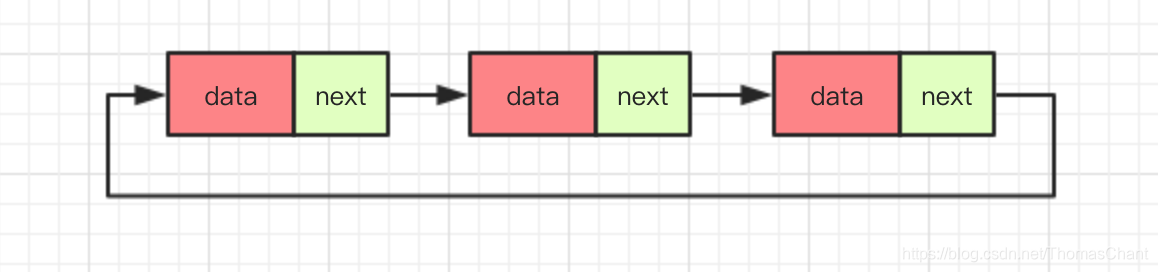
双向循环链表

双向循环链表是双向链表和循环链表的组合，同时拥有双向链表和循环链表的优点。

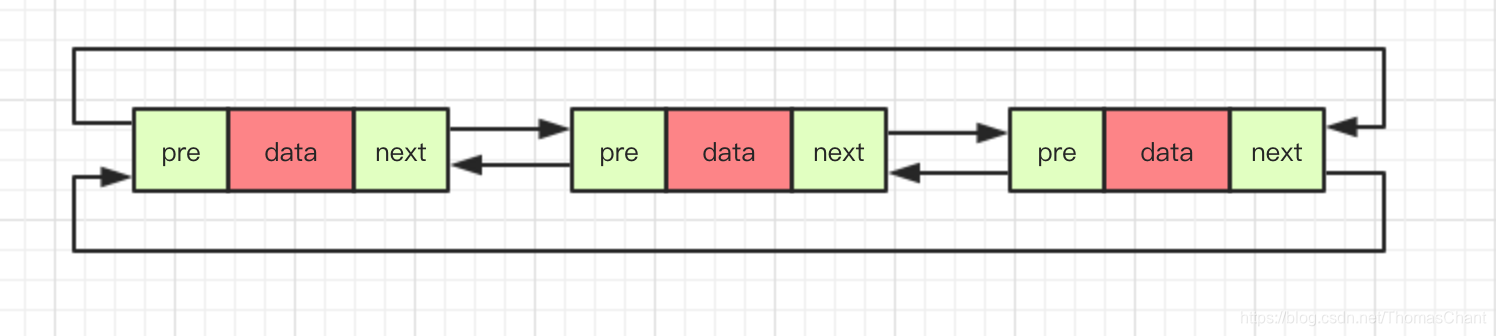
链表与数组对比

	索引访问	查找	头部插入/删除	中间插入/删除	尾部插入/删除
数组	O(1)	O(n)	O(n)	O(n)	O(1)
链表	O(n)	O(n)	O(1)	查找时间+O(1)	节点已知O(1)，未知O(n)

说明：
1.对于链表，在中间插入或删除一个节点，时间复杂度依赖于找到这个节点(对于单向链表来讲是其前节点)的时间，如果这个节点已知，那么删除或插入只需要常数级的时间复杂度。
2.在尾部插入或删除节点，对于双向链表（包括双向循环链表）时间复杂度是常数级别的，因为尾节点已知，对于单向链表（包括单向循环链表）由于尾节点未知需要查找，插入或删除时间复杂度为O(n)。