《百面机器学习》学习笔记之经典算法(支持向量机SVM、逻辑回归LR、决策树DT)

第三章 经典算法

01 支持向量机

支持向量机（Support Vector Machine, SVM）是监督学习方法。

将低维的数据映射到高维的核映射空间，寻找“分类超平面”将不同类别的数据区分开。

在空间上线性可分的两类点，分别向SVM分类的超平面上做投影，这些点在 超平面上的投影仍然是线性可分的吗？

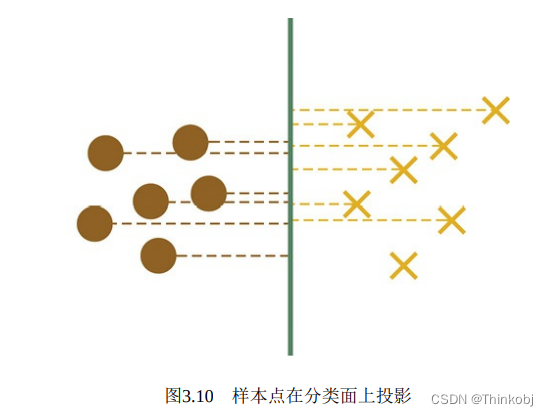
从图中可以看出，二维空间中的点进行投影时，并不是线性可分的。

但实际上，对于任意线性可分的两组点，它们在SVM分类的超平面上的投影 都是线性不可分的。

是否存在一组参数使SVM训练误差为0？

一个使用高斯核 $K(x,z)=e-||x-z|{|}^{2/r^2}$训练的SVM中，试证明若给定训练集中不存在两个点在同一位置，则存在一组参数${\alpha }_1,...,{\alpha }_m,b$以及参数$\gamma$使得SVM的训练误差为0

通过证明得到，对于任意$x^{(j)}$，预测结果$f(x^{(j)})$与样本真实标签$y^{(j)}$的距离小于1。注意到，$y^{(j)}\in (1，-1)$，当训练样本为正例，即$y^{(j)}=1$时，预测结果$f(x^{(j)})>0$，样本被预测为正例；而当训练样本为负例，即$y^{(j)}=-1$时，预测结果$f(x^{(j)})<0$，样本被预测为负例。因此所有样本的类别都被正确预测，训练误差为0。所以，存在一组参数使SVM训练误差为0.

训练误差为0的SVM分类器一定存在吗？

虽然在上述问题中我们找到了一组参数$\alpha 1,...,\alpha m,b$以及$\gamma$使得SVM的训练误差为0，但这组参数不一定是满足SVM条件的一个解。在实际训练一个不加入松弛变量的SVM模型时，是否能保证得到的SVM分类器满足训练误差为0呢？

通过证明得到，对任意$j$有$y^{(j)}f(x^{(j)})>1$,满足SVM解的条件。因此SVM最优解也满足上述条件，同时一定使模型分类误差为0

加入松弛变量的SVM的训练误差可以为0吗？

在实际应用中，如果使用SMO算法来训练一个加入松弛变量的线性SVM模型，并且惩罚因子C为任一未知常数，我们是否能得到训练误差为0的模型呢？

分析：使用SMO算法训练的线性分类器并不一定能得到训练误差为0的模型。这是由于我们的优化目标改变了，并不再是使用训练误差最小。考虑带松弛变量的SVM模型优化的目标函数所包含的两项：$C{\sum }_{i=1}^m{\xi }_i$和$\frac{1}{2}\Vert w^2\Vert$，当我们的参数C选取较小的值时，后一项（正则项）将占据优化的较大比重。这样，一个带有训练误差，但是参数较小的点将成为更优的结果。一个简单的特例是，当C取0时，$w$也取0即可达到优化目标，但是显然此时我们的训练误差不一定能达到0

02 逻辑回归

逻辑回归相比于线性回归，有何异同？

逻辑回归（Logistic Regression）处理的是分类问题，线性回归处理的是回归问题，这是两者的最本质区别。逻辑回归中，因变量取值是一个二元分布，模型学习得出的是$E\left [ y|x;\theta \right ] $，即给定自变量和超参数后，得到因变量的期望，并基于此期望来处理预测分类问题。而线性回归中实际上求解的是，$$y^{\prime }={\theta }^{T}x$$，是对我们假设的真实关系$$y={\theta }^{T}x+\epsilon$$的一个近似，其中$$\epsilon$代表误差项，我们使用这个近似项来处理回归问题。

逻辑回归中的因变量为离散的，而线性回归中的因变量是连续的

当然逻辑回归和线性回归也不乏相同之处，首先我们可以认为二者都使用了
极大似然估计来对训练样本进行建模。线性回归使用最小二乘法，实际上就是在
自变量$x$与超参数$\theta$确定，因变量$y$服从正态分布的假设下，使用极大似然估计的一个化简；而逻辑回归中通过对似然函数$L(\theta )={\prod }_{i=1}^{N}P(y_i|x_i;\theta )={\prod }_{i=1}^N(\pi (x_i){)}^{y_i}(1-\pi (x_i){)}^{(1-y_i)}$的学习，得到最佳参数θ。另外，二者在求解超参数的过程中，都可以使用梯度下降的方法，这也是监督学习中一个常见的相似之处。

当使用逻辑回归处理多标签的分类问题时，有哪些常见做法，分别应用于哪些场景，它们之间又有怎样的关系？

如果一个样本只对应于一个标签，我们可以假设每个样本属于不同标签的概率服从于几何分布，使用多项逻辑回归进行分类
$$h_{\theta }(x)=\left[\begin{array}{c}p(y=1|x;\theta )\\ p(y=2|x;\theta )\\ ⋮\\ p(y=k|x;\theta )\end{array}\right]=\frac{1}{{\sum }_{j=1}^k{e}^{{\theta }_j^{T}x}}\left[\begin{array}{c}{e}^{{\theta }_1^{T}x}\\ e^{{\theta }_2^{T}x}\\ ⋮\\ e^{{\theta }_k^{T}x}\end{array}\right]$$

其中${\theta }_1,{\theta }_2,...,{\theta }_k\in {\mathbb{R}}^{\mathbb{k}}$为模型的参数，而${\sum }_{j=1}^k{e}^{{\theta }_j^{T}x}$可以看作是对概率的归一化。一般来说，多项逻辑回归具有参数冗余的特点，即将${\theta }_1,{\theta }_2,...,{\theta }_k$同时加减一个向量后预测结果不变。特别地，当类别数为2时，
$$h_{\theta }(x)=\frac{1}{e^{{\theta }_1^{T}x}+e^{{\theta }_2^{T}x}}\left[\begin{array}{c}{e}^{{\theta }_1^{T}x}\\ e^{{\theta }_2^{T}x}\end{array}\right]$$
将所有参数减去${\theta }_1$,上式变为
$$h_{\theta }(x)=\frac{1}{e^{0\cdot x}+e^{({\theta }_2^T-{\theta }_1^T)x}}\lceil \begin{array}{c}{e}^{0\cdot x}\\ e^{({\theta }_2^T-{\theta }_1^T)x}\end{array}\rceil =\lceil \begin{array}{c}\frac{1}{1+e^{{\theta }^{T}x}}\\ 1-\frac{1}{1+e^{{\theta }^{T}x}}\end{array}\rceil$$
其中$\theta ={\theta }_2-{\theta }_1$。整理后地式子与逻辑回归一致。
因此，多项逻辑回归实际上是二分类逻辑回归在多标签分类下的拓展。

当存在样本可能属于多个标签的情况时，我们可以训练k个二分类的逻辑回归分类器。第i个分类器用以区分每个样本是否可以归为第i类，训练该分类器时，需要把标签重新整理为“第i类标签”与“非第i类标签”两类。通过这样的办法，我们就解决了每个样本可能拥有多个标签的情况。

03决策树

决策树是一种自上而下，对样本数据进行树形分类的过程，由结点和有向边组成。结点分为内部结点和叶结点，其中每个内部结点表示一个特征或属性，叶结点表示类别。决策树作为最基础、最常见的有监督学习模型，常被用于分类问题和回归问题。

一般而言，决策树的生成包含了特征选择、树的构造、树的剪枝三个过程。

决策树有哪些常用的启发函数？

从若干不同的决策树中选取最优的决策树是一个NP完全问题，在实际中通常会采用启发式学习的方法构建一颗满足启发式条件的决策树。

常用的决策树算法有ID3、C4.5、CART

ID3—最大信息增益

对于样本集合D，类别数为K，数据集D的经验熵表示为$$H(D)=-\sum _{k=1}^K\frac{|C_k|}{|D|}{\log }_2\frac{|C_k|}{|D|}$$

其中$C_k$是样本集合D中属于第$k$类的样本子集，$|C_k|$表示该子集的元素个数，$|D|$表示样本集合的元素个数。

然后计算某个特征A对于数据集D的经验条件熵$H(D|A)$为
$$H(D|A)=\sum _{i=1}^n\frac{|D_i|}{|D|}H(D_i)=\sum _{i=1}^n\frac{|D_i|}{|D|}(-\sum _{k=1}^K\frac{|D_{ik}|}{|D_i|}{\log }_2\frac{|D_{ik}|}{|D_i|})$$

其中$D_i$表示D中特征A取第i个值得样本子集，$D_{ik}$表示$D_i$中属于第k类的样本子集。

于是信息增益$g(D,A)$可以表示为二者之差，可得

$$g(D,A)=H(D)-H(D|A)$$

C4.5—最大信息增益比

特征A对于数据集D得信息增益比定义为

$$g_R(D,A)=\frac{g(D,A)}{H_A(D)}$$

其中，$$H_A(D)=-\sum _{i=1}^n\frac{|D_i|}{|D|}{\log }_2\frac{|D_i|}{|D|}$$称为数据集D关于A的取值熵。

CART—最大基尼指数（Gini）

Gini描述的是数据的纯度，与信息熵含义类似

$Gini(D)=1-{\sum }_{k=1}^n(\frac{|C_k|}{|D|}{)}^2$

CART在每一次迭代中选择基尼指数最小的特征及其对应的切分点进行分类。但与ID3、C4.5不同的是，CART是一颗二叉树。特征A的Gini指数定义为

$$Gini(D|A)=\sum _{i=1}^n\frac{|D_i|}{|D|}Gini(D_i)$$

（1）ID3是采用信息增益作为评价标准，信息增益反映的是给定条件以后不确定性减少的程度，即条件熵越小，信息增益越大。

C4.5实际上是对ID3进行优化，通过引入信息增益比，一定程度熵对取值比较多的特征进行惩罚，避免ID3出现过拟合的特征，提升决策树的泛化能力。

（2）ID3只能处理离散型变量，而C4.5和CART都可以处理连续型变量。

C4.5处理连续型变量时，通过对数据排序之后找到类别不同的分割线作为切分点，根据切分点把连续属性转换为布尔型，从而将连续型变量转换多个取值区间的离散型变量。

CART因为每次都会对特征进行二值划分，所以可以很好地适用于连续型变量。

（3）ID3和C4.5只能用于分类任务，而CART（Classification and Regression Tree， 分类回归树）

（4）ID3对样本特征缺失值比较敏感，而C4.5和CART可以对缺失值进行不同方式地处理。

（5）ID3和C4.5可以在每个结点上产生出多叉分支，且每个特征在层级之间不会复用，而CART每个结点只会产生两个分支。

（6）ID3和C4.5通过剪枝来权衡树的准确性与泛化能力，而CART直接利用全部数据发现所有可能的树结构进行对比。

如何对决策树进行剪枝？

决策树的剪枝通常有两种方法，预剪枝（Pre-Pruning）和后剪枝（Post-Pruning）

预剪枝，即在生成决策树的过程中提前停止树的增长。常用的方法有：

（1）当树到达一定深度的时候，停止树的生长。

（2）当到达当前结点的样本数量小于某个阈值的时候，停止树的生成。

（3）计算每次分裂对测试集的准确度提升，当小于某个阈值的时候，不再继续扩展。

后剪枝，让算法生成一颗完全生长的决策树，然后从最底层向上计算是否剪枝。后剪枝方法通常可以得到泛化能力更强的决策树，但时间开销会更大。

常见的后剪枝方法包括错误率降低剪枝（Reduced Error Pruning, REP）、悲观剪枝（Pessimistic Error Pruning, PEP）、代价复杂度剪枝（Cost Complexity Pruning, CCP）、最小误差剪枝（Minimum Error Pruning, MEP）、CVP（Critical Value Pruning）、OPP（Optimal Pruning）等方法。

CART剪枝方法CCP代价复杂剪枝主要包含以下两个步骤：

（1）从完整决策树$T_0$开始，生成一个子树序列$$T_0,T_1,T_2,...,T_n$，其中$T_{i+1}$由$T_i$生成，$T_n$为树的根结点。

（2）在子树序列中，根据真实误差选择最佳的决策树

步骤（1）从$T_0$开始，裁剪$T_i$中关于训练数据集合误差增加最小的分支以得到$T_{i+1}$。具体地，当一棵树T在结点t处剪枝时，它地误差增加可以用$R(t)-R(T_t)$表示，其中$R(t)$表示进行剪枝之后地该结点误差，$R(T_t)$表示未进行剪枝时子树$T_t$的误差。考虑到树的复杂性因素，我们用$|L(T_t)|$表示子树$T_t$的叶子结点个数，则树在结点t处剪枝后的误差增加率为

$\alpha =\frac{R(t)-R(T_t)}{|L(T_t)|-1}$

在得到$T_i$后，我们每步选择$\alpha$最小的结点进行相应剪枝。