Mondriaan's Dream （POJ - 2411，状压 DP）

最新推荐文章于 2021-08-10 19:37:33 发布

原创最新推荐文章于 2021-08-10 19:37:33 发布 · 304 阅读

1 ·

CC 4.0 BY-SA版权

状压 DP 专栏收录该内容

6 篇文章

订阅专栏

本文探讨了在n*m大小的棋盘上摆放大小为2*1的木块的不同方法，通过动态规划解决该问题，详细解析了状态转移方程及代码实现。

一.题目链接：

POJ-2411

二.题目大意：

有一个 n*m 大小的棋盘，往上摆满大小为 2*1 大小的木块，问有多少种不同的方法.

三.分析：

首先，明确一件事情：只需统计横放木块的合法方案数，对于一个合法横放木块状态来说，竖放木块只需插空即可，方案数为一.

设 dp[i][j] 表示横放木块放完了 1~ i-1 列，且第 i 列状态为 j 的方案数.

第 i 列的状态 j 是指第 i-1 列所横放的木块伸到第 i 列的二进制状态表示.

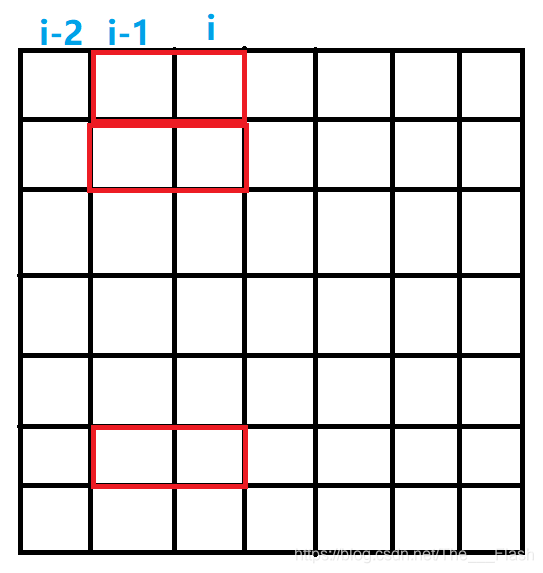
如上图，第 i 列的状态 j 为 1100010.

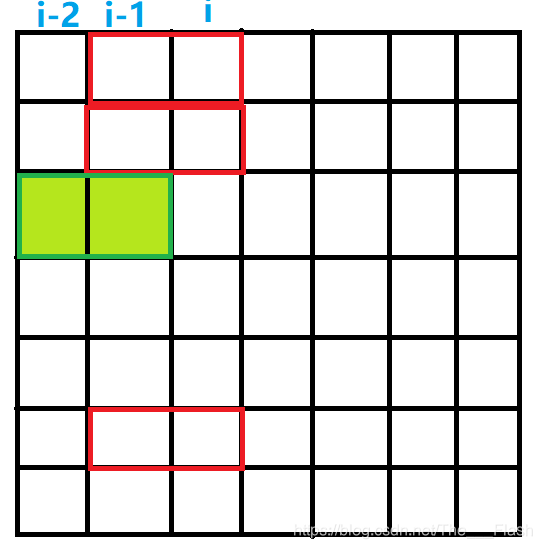
设第 i - 1 列的状态为 k.

易得合法的状态转移关系应满足一下两个条件：

① (j & k) == 0, 保证两个横放木块不会交叉.

② (j | k) 不能有奇数个连续的 0，保证了竖放木块能填满空格.

对于第二点，我们可以预处理出那些状态是合法的.

时间复杂度为 $O(4^{n}m)$

四.代码实现：

#include <cstdio>
#include <cstring>
using namespace std;

typedef long long ll;

const int M = (int)11;

bool valid[(1<<M) + 5];
ll dp[M + 5][(1<<M) + 5];

void init(int n)
{
    for(int i = 0; i < (1<<n); ++i)
    {
        bool have_odd = 0, cnt = 0;
        for(int j = 0; j < n; ++j)
        {
            if((i>>j) & 1)
                have_odd |= cnt, cnt = 0;
            else
                cnt ^= 1;
        }
        valid[i] = !(have_odd | cnt);
    }
}

int main()
{
//    freopen("input.txt", "r", stdin);
    int n, m;
    while(~scanf("%d %d", &n, &m) && (n + m))
    {
        init(n);
        memset(dp, 0, sizeof(dp));
        dp[0][0] = 1;
        for(int i = 1; i <= m; ++i)
        {
            for(int j = 0; j < (1<<n); ++j)
            {
                for(int k = 0; k < (1<<n); ++k)
                {
                    if(!(j & k) && valid[j | k])
                    {
                        dp[i][j] += dp[i - 1][k];
                    }
                }
            }
        }
        printf("%lld\n", dp[m][0]);
    }
    return 0;
}