算法导论——函数的增长

最新推荐文章于 2021-10-15 17:58:15 发布
最新推荐文章于 2021-10-15 17:58:15 发布
阅读量639 收藏 1
点赞数 2
CC 4.0 BY-SA版权
分类专栏： 算法 文章标签： 算法效率 函数增长 算法导论 运行时间描述
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/The_Only_God/article/details/95306282
博客围绕函数的增长展开，介绍了算法运行时间描述的渐进记号，如Θ、O、Ω、o、ω记号，分别对应渐进紧确界、渐进上界、渐进下界、非渐进紧确上界和非渐进紧确下界。还提及取整、模运算等数学知识，以及多项式、指数等函数的比较。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

文章目录

函数的增长

渐进记号

输入规模对运行时间的函数

Θ记号

在这里插入图片描述
若存在正常量c1和c2，使得对于足够大的n,函数f(n)能“夹入”c1g(n)与c2g(n)之间，则f(n)属于集合Θ(g(n))。 称g(n)是f(n)的一个渐进紧确界。（f(n)为算法运行时间。）

O记号

在这里插入图片描述
函数只有一个渐进上界时，使用O记号。
O(n)限制了算法的最坏运行时间。

Ω记号

在这里插入图片描述
Ω限制了渐进下界，即最好运行时间。

o记号

非渐进紧确的上界
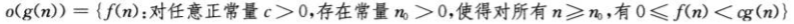
在这里插入图片描述
在这里插入图片描述

ω记号

非渐进紧确的下界
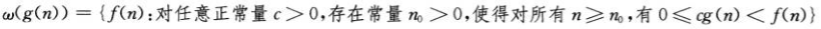
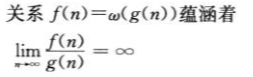
在这里插入图片描述
在这里插入图片描述

数学知识

取整

在这里插入图片描述

模运算

在这里插入图片描述

函数及其比较

多项式

在这里插入图片描述

指数

在这里插入图片描述
比较
在这里插入图片描述

对数

在这里插入图片描述
比较

阶乘

在这里插入图片描述

多重函数

在这里插入图片描述

多重对数函数

在这里插入图片描述
在这里插入图片描述

斐波那契数

在这里插入图片描述

函数比较总结

a^n(0<a<1)、 常数、对数、多项式、指数、阶乘、n^n

《算法导论》学习分享——3. 函数的增长
MaoMao-go
03-10 476
3. 函数的增长 本章给出集中标准方法来简化算法的渐进分析。 渐进符号 Θ 渐进紧确界    f(n)=Θ(g(n))f(n)=\Theta(g(n))f(n)=Θ(g(n)) 类似于 a = b    当n&gt;n0时，存在常数c1和c2使得c1·g(n) &lt;= f(n) &lt;= c2·g(n) Ο 渐进上界    f(n)=O(g(n))f(n)=O(g(n))f(n)=O(g(...
算法导论 学习笔记 第三章 函数的增长
苏雅乐图的博客
07-27 856
这一章讲了两大部分。第一部分是讲了渐进符号，有theta，bigO，bigΩ，littleo，littleΩ。第二部分讲了几个常见的数学知识。渐进符号Θ符号渐进符号表示的都是算法的输入规模无限大的时候的运行时间的增长率。 例如：f(n) = Θ(n^2) 表示的是在n足够大的时候f(n)的增长率是差不多n的二次方。下面给出准确定义： Θ(g(n)) = {f(n):存在两个常数c1和
冒泡排序
omygege
07-02 193
1. 实现基本原理 2 实现代码 1.实现基本原理 2. 实现代码 usingSystem;usingSystem.Collections.Generic;usingSystem.Linq;usingSystem.Text;namespaceFindMissingNumber{//冒泡排序classBubbleSort{publicstaticvoidSort(refint[]arr){i...
算法导论--函数的增长
jiangbinbin的博客
01-30 1601
3.函数的增长 1.渐近记号 我们将主要使用渐进记号来描述算法的运行时间。渐进记号实际上应用于函数。 θ(n2)=an2+bn+c 这个是插入排序的运行时间表达，我们使用θ（n2）来表示。 我们使用渐近记号来刻画算法的运行时间。 （1） θ 记号 插入排序的最坏运行时间为：T(n) = θ(n²)。 让我们来定义这个记号意指什么。 对于一个给定的函数g(n),用θ(g(n))来表示...
函数的增长
diandingyin9417的博客
05-17 175
1：渐进记号 我们主要用渐进记号来描写叙述算法的执行时间 Θ记号：如Θ（g(n)） 是函数的一个渐进紧确界 O记号：如O（g(n)） 是函数的一个渐进紧确上界 o记号：如o（g(n)） 是函数的一个渐进紧确上界 Ω记号：如Ω（g(n)） 是函数的一个渐进紧确下界 w记号：如w（g(n)） 是函数的一个渐进紧确下界 渐进函数性质： ...
2020.11.16——函数、层叠上下文
weixin_43415330的博客
11-16 261
JS基础 && CSS面试题 -2020.11.16 a. JS基础 i. 了解JS中的函数，什么是函数，判断函数的方法，函数调用的方式，与之对应的this在函数中的使用， this的几种取值，如何创建函数，了解特殊函数（匿名函数， IIFE（立即执行函数表达式））， 箭头函数， 箭头函数和普通函数的区别，函数的参数（arguments） 函数 函数实际上是对象。每个函数都是 Function类型的实例，而 Function 也有属性和方法，跟其他引用类型一样。 因为函数是对
算法导论——习题解答
02-26
通过上述章节内容的概述，我们可以看出，《算法导论——习题解答》不仅是一本配套教材的习题解答集，更是一部系统学习算法设计与分析的宝贵资源。通过深入浅出的讲解和丰富的习题解答，本书能够帮助读者建立起坚实的...
算法导论——教师手册
11-10
《算法导论》是一部经典而全面的算法教材，适合计算机科学领域的本科生和研究生学习使用。本教师手册旨在为授课教师提供教学辅助资料，包括详细的讲义和解题指南等。 #### 二、章节内容详解 **1. 第2章：入门** -...
算法导论——课后思考题
04-14
#### 算法导论概览与重要性 《算法导论》是一本经典的计算机科学教材，由Thomas H. Cormen、Charles E. Leiserson、Ronald L. Rivest和Clifford Stein共同编写。本书深入浅出地介绍了算法设计与分析的基本概念和...
函数增长
zy_zprz的博客
03-19 1740
1、渐进记号Θ记号对一个给定的函数g(n)，用Θ(g(n))来表示函数的集合:Θ(g(n)) = {f(n):存在一个正常量c1,c2和n0，使得对所有的n &gt;= n0，有0 &lt;= c1g(n) &lt;= f(n) &lt;= c2g(n)}。即，存在常量c1和c2使得足够大的n，函数f(n)能“夹入”c1g(n)与c2g(n)之间，则f(n)属于集合Θ(g(n))。通常记做f(n)...
算法导论-函数的增长
ywj1987926的博客
04-04 359
虽然我们能够精确的计算出一个算法的精确运行时间,但是通常来说这种精确的计算是没有必要的。我们一般只考虑到输入数据规模足够大时的情况，也就是当输入规模无限增加时，算法的运行时间如何随着输入规模的变大而增加。因此算法的运行时间一般都是利用渐进记号来表示的，以下是几种标准方法来简化算法的渐近分析。 1.渐近记号         可以理解为这个渐近符号表示的g(n)决定了f(n)的上限和下
《算法导论3rd第三章》函数增长
懒猫的脚印
10-15 1297
算法导论 第三章 函数增长
《算法导论》第3章：函数的增长
Salmon_lee的博客
02-11 350
这章主要展现了一些基本函数的知识，引入了渐进记号的概念。一些陌生的知识点：①lg* x：就是“劳格”i次得到一个小于等于1的数；②Stiring公式：n! ≈ sqrt(2πn)*(n/e)^nn! = o(n^n)，n! = w(2^n)，lg(n!) = θ(lg(n^n))；③斐波那契数列的Fi为Φ^i/sqrt(5)舍入到最近的整数，其中Φ为x²-x-1=0的正根；④取整函数的有关性质(p...
《算法导论》第三章 函数的增长
Time_Limit的博客
01-31 667
目录第三章 函数的增长3-1 知识点Θ\ThetaΘ记号O\OmicronO记号Ω\OmegaΩ记号不是所有函数都可渐进比较练习题3.1-13.1-23.1-33.1-43.1-53.1-73.1-83.2-13.2-23.2-33.2-43.2-53.2-73.2-8思考题 3-1思考题 3-2思考题 3-3思考题 3-4 第三章 函数的增长 3-1 知识点 Θ\ThetaΘ记号 Θ(g(n))\Theta(g(n))Θ(g(n))的含义为：存在正常量c1,c2和n0c_1,c_2 和 n_0c1​,c2
成长函数
weixin_30555125的博客
06-28 383
$P(|E_{in}-E_{out}|>\epsilon) \leq 2Me^{-2\epsilon^2N}$ 当M小时，能够保证Ein和Eout差不多，但是找不到比较小的Ein当M很大时，能找到比较小的Ein，但是不能保证Ein和Eout差不多 所以，希望可以找到一个比较适合的M $m_H$表示和假设集H相关的假设数量$P(|E_{in}-E_{out}|>\eps...
第 3 章 函数的增长
gastation的博客
06-07 1138
当输入规模足够大时，使得只有运行时间的增长量级有关时，我们要研究算法的渐近效率。也就是说，我们关心当输入规模无限增加时，在极限中，算法的运行时间如何随着输入规模的变大而增加。通常，渐近地更有效的某个算法对很小的输入外的所有情况将是最好的。 　　本章给出几种标准方法来简化算法的渐近分析。下一节首先定义几类“渐近记号”，其中，我们已经见过一个例子是Θ记号。然后，我们给出贯穿本书使用的几种记号的约定。
掌握算法精髓——《算法导论》第四版英文答案解析
标题《算法导论答案第四版英文版》中提到的《算法导论》是由Thomas H. Cormen、Charles E. Leiserson、Ronald L. Rivest和Clifford Stein编写的经典计算机科学教材，广泛应用于高校计算机科学与工程专业的教学中。...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值