动态规划：72. 编辑距离

72. 编辑距离

题目要求：

解题思路：

 根据动态规划的步骤：

1. 定义数组元素的含义，这里用到两个字符串，所以应该定义二维数组；

由于我们求的是字符串1转换成字符串2所需要的最少次数：当字符串1的长度为i，字符串2的长度为j，则字符串1转换成字符串2所需次数为dp[i][j];

2. 找出关系数组之间的关系式；

大部分情况下， dp[i] [j] 和 dp[i-1] [j]、 dp[i] [j-1]、 dp[i-1] [j-1] 肯定存在某种关系。

这里题目也给出了提示：插入，删除，替换操作

大体上分三种情况：

1)替换的情况：当word1中的前i-1个就可以变换为word2中的前j-1个，那么我们只要根据word1中的第i个是否等于word2中的第j个字符进行判断，

如果相等，那么cost[i][j]=cost[i-1][j-1];  否则，cost[i][j]=cost[i-1][j-1]+1,加的1就是我们将word1中第i个字符替换为word2中第j个的消耗。

2)删除的情况：当word1中的前i-1个就可以变换为word2中的前j个时，我们需要将word1中的第i个字符删除，cost[i][j]=cost[i-1][j]+1；

3)增加的情况：当word1中的前i个可以变换为word2中的前j-1个时，我们需要将word1中的第i个字符后面增加一个，cost[i][j]=cost[i][j-1]+1；

所以，我们的cost[i][j]取上列的最小值即可。

 1 class Solution {
 2 public:
 3     int minDistance(string word1, string word2) 
 4     {
 5         int m = word1.length();
 6         int n = word2.length();
 7         int dp[m+1][n+1];　　　　　　//相对下面两个，比较省内存
 8         //vector<vector<int>>dp(m+1,vector<int>(n+1,0));  //非常耗内存
 9         //动态申请数组二维dp  大小：(m+1)*(n+1)　　　　　　　　　//耗内存
10         // int **dp = new int*[m+1]; 
11         // for(int i=0; i<=m; i++) 
12         // {
13         //     dp[i] = new int[n+1];
14         // }
15         dp[0][0] = 0;
16         for (int i=1; i <= m; i++)
17         {
18             //dp[i][0] = dp[i-1][0] + 1;
19             dp[i][0] = i;
20         }  
21         for (int i=1; i <= n; i++)
22         {
23             //dp[0][i] = dp[0][i-1] + 1;
24             dp[0][i] = i;
25         }  
26         for (int i=1; i <= m; i++)
27         {
28             for (int j=1; j <= n; j++)
29             {           
30                 //strcmp(word1.c_str(),word2.c_str())
31                 if (word1[i-1]==word2[j-1])
32                 {
33                     dp[i][j] = dp[i-1][j-1];
34                 }
35                 else 
36                 {
　　　　　　　　　　　　　　//无需手动写函数，直接使用C++中自动的宏定义：#define min(a,b) ( ((a)>(b)) ? (b):(a) ) 
37                     dp[i][j]=min(min(dp[i-1][j-1], dp[i][j-1] ), dp[i-1][j] ) + 1;
38                 }
39             }
40         }
41         return dp[m][n];
42     }
43 
44     // int mindata(int a, int b)
45     // {
46     //     return ((a > b)? b:a);
47     // }
48 };

动态规划的优化：

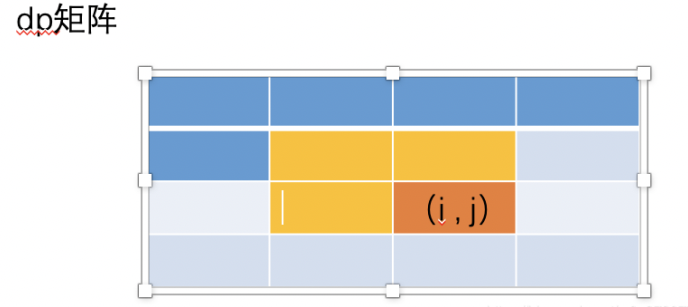
解题思路：一定要画图(矩阵图)，看哪些网格可以替换，从而将二维数组转变成一维数组。

根据公式：dp[j] = min( min(dp[j-1], dp[j]), pre) + 1; 

每次计算dp[i][j]时用到三个网格，分别是(i-1，j-1)，(i-1，j)和 (i，j-1)，这时最多只需要i-1行网格，那么通过临时变量将(i-1，j-1)保存，并且每次将计算结果(i，j)更新到(i-1，j)中。

 1 class Solution {
 2 public:
 3     int minDistance(string word1, string word2) 
 4     {
 5         int m = word1.length();
 6         int n = word2.length();
 7         int dp[n+1];
 8         //vector<vector<int>>dp(m+1,vector<int>(n+1,0));
 9         //动态申请数组二维dp  大小：(m+1)*(n+1)
10         // int **dp = new int*[m+1]; 
11         // for(int i=0; i<=m; i++) 
12         // {
13         //     dp[i] = new int[n+1];
14         // }
15         //dp[0] = 0;
16         for (int i=0; i <= n; i++)
17         {
18             dp[i] = i;
19         } 
20         for (int i=1; i <= m; i++)
21         {
22             int tmp = dp[0];
23             dp[0] = i;       
24             for (int j=1; j <= n; j++)
25             {
26                 int pre = tmp;      //需要计算的值
27                 tmp = dp[j];        //在数据覆盖之前，先保存
28                 if (word1[i-1]==word2[j-1])
29                 {
30                     dp[j] = pre;
31                 }
32                 else
33                 {
34                     dp[j] = min( min(dp[j-1], dp[j]),  pre) + 1;
35                 } 
36             }
37         } 
38         return dp[n];
39     }
40 };