递归训练2：求两个有序数组的第K小数

最新推荐文章于 2025-12-16 14:17:05 发布

原创最新推荐文章于 2025-12-16 14:17:05 发布 · 47 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法

本文介绍了一种高效算法，用于在两个已排序数组中找到第k小的元素。通过递归方式，每次比较两数组中点位置的值，逐步缩小搜索范围，达到O(log(min(m,n)))的时间复杂度。

解题思路：

开始思路想的是两个数组有序，通过两个数组相互对比，那么把寻找第k小的数转换成选择最小数，找到之后跳过，然后循环k次，这样必须循环k次，而且每次还要对比，时间复杂度太高。

优化之后，解题思路与下面这个很类似。

递归训练1：在两个长度相等的排序数组中找到上中位数

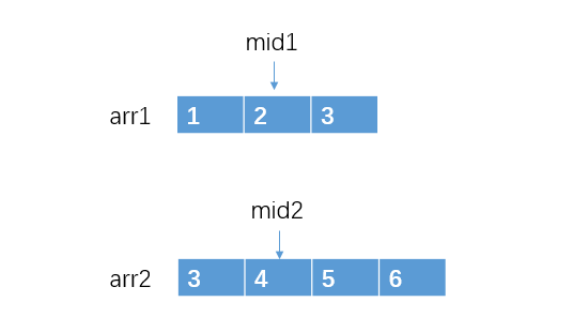
每次寻找时，将两个数组mid1=k/2；mid2=k/2；

此时 arr2[mid2] > arr1[mid1]，那么问题转化为在数组 arr1[mid1+1...m1]和数组 arr2[0...m2] 寻找第
(K-md1-1)小的元素。 (这类似于二分查找，效率比较高)

这里k从0开始算起，也就是第0小元素开始，令k=k-1；

不过这里需要注意的是，有可能 k/2 的值是⼤于 m1 或者 m2的，所以如果 k/2 > m1 或者 m2 的话，我
们直接令 md1 = m1-1 或者 md2 = m2-1 就行了。

 1 class Solution {
 2 public:
 3     int get_k_min(int arr1[], int arr2[], int k) 
 4     {
 5         int data;
 6         if (arr1==NULL || arr1.length < 1)
 7         {
 8             return arr2[k-1];
 9         }
10         if (arr2==NULL || arr2.length < 1)
11         {
12             return arr1[k-1];
13         }
14         data = k_min(arr1, 0, arr1.length-1, arr2, 0 arr2.length-1, k-1);
15         return data;
16     }
17 
18 int  k_min(int arr1[], int L1, int R1, int arr2, int L2, int R2, int k)
19 {
20     //递归结束条件，是否超出数组大小
21     if (L1 > R1)
22     {
23         return arr2[L1+k];
24     }
25     if (L2 > R2)
26     {
27         return arr1[L1+k];
28     }
29     //递归结束，寻找到第k个小的数
30     if (k==0)
31     {
32         if (arr1[L1] <arr2[L2])
33         {
34             return arr1[L1];
35         }
36         if (arr1[L1] >arr2[L2])
37         {
38             return arr2[L2];    
39         }
40         return arr1[L1];    //return arr2[L2];
41     }
42 
43     int mid1 = L1 + k/2 < R1 ? L1 + k/2:R1;
44     int mid2 = L2 + k/2 < (R2-L1) ? L2 + k/2:R2;
45     if (arr1[mid1] < arr2[mid2])
46     {
47         k_min(arr1, mid1+1, R1, arr2, L2, R2, k-k/2-1);
48     }
49     else if (arr1[mid1] > arr2[mid1])
50     {
51         k_min(arr1, L1, R1, arr2, mid2, R2, k-k/2-1);
52     }
53     else
54         return arr1[mid1];    //return arr2[mid2];
55 }
56 
57 };