【代码随想录算法训练营Day26】● 39. 组合总和；● 40.组合总和II；● 131.分割回文串

Day 26 第七章 回溯算法part03

• 今日内容
  • ● 39. 组合总和
  • ● 40.组合总和II
  • ● 131.分割回文串

39. 组合总和

• 本题是 集合里元素可以用无数次，那么和组合问题的差别 其实仅在于 startIndex上的控制
• 题目链接：https://leetcode.cn/problems/combination-sum/
• 视频讲解：https://www.bilibili.com/video/BV1KT4y1M7HJ
• 文章讲解：https://programmercarl.com/0039.%E7%BB%84%E5%90%88%E6%80%BB%E5%92%8C.html

思路

先用自己和自己组合，直到超出target再回溯与别的数组合

剪枝

剪枝条件：当剩余备选数都比需要的数小时就不用遍历了

代码

public static List<List<Integer>> combinationSum(int[] candidates, int target) {
	List<List<Integer>> res = new ArrayList<>();
	dfs(0, candidates, target, new LinkedList<>(), res);
	return res;
}
public static void dfs(int start, int[] candidates, int target, LinkedList<Integer> stack, List<List<Integer>> res){
	//加入剪枝后就不需要判断这个了，因为target一定大于candidate
	//if(target < 0) return;
	if(target == 0){
		res.add(new ArrayList<>(stack));
		return;
	}
	for (int i = start; i < candidates.length; i++) {
		int candidate = candidates[i];
		//❗剪枝操作
		if(target < candidate) continue;
		stack.push(candidate);
		dfs(i, candidates, target - candidate, stack, res);
		stack.pop();
	}
}

40.组合总和II

• 本题开始涉及到一个问题了：去重。
• 注意题目中给我们 集合是有重复元素的，那么求出来的 组合有可能重复，但题目要求不能有重复组合。
• 题目链接：https://leetcode.cn/problems/combination-sum-ii/
• 视频讲解：https://www.bilibili.com/video/BV12V4y1V73A
• 文章讲解：https://programmercarl.com/0040.%E7%BB%84%E5%90%88%E6%80%BB%E5%92%8CII.html

思路

与39几乎一模一样，区别在于

• 1️⃣数组中的某个元素不能重复使用（类似46&47）
  • 类似组合与排序的区别，递归中start + 1即可
• 2️⃣结果不能有重复的集合
  • 先排序，然后规定相同数中后面的必须在前面的被使用后才能使用

代码

public static List<List<Integer>> combinationSum2(int[] candidates, int target) {
	List<List<Integer>> res = new ArrayList<>();
	//2️⃣改动二
	Arrays.sort(candidates);
	dfs(0, candidates, new boolean[candidates.length], target, new LinkedList<>(), res);
	return res;
}
//2️⃣改动二，加入判断数是否被用过的数组visited
public static void dfs(int start, int[] candidates, boolean[] visited,int target, LinkedList<Integer> stack, List<List<Integer>> res){
	//加入剪枝后就不需要判断这个了，因为target一定大于candidate
	//if(target < 0) return;
	if(target == 0){
		res.add(new ArrayList<>(stack));
		return;
	}
	for (int i = start; i < candidates.length; i++) {
		int candidate = candidates[i];
		//剪枝操作
		if(target < candidate) continue;
		//2️⃣改动二，如果前一个数与当前数一样且没被用过就跳过
		if(i > 0 && candidate == candidates[i - 1] && !visited[i - 1]) continue;
		visited[i] = true;
		stack.push(candidate);
		//1️⃣改动一
		dfs(i + 1, candidates, visited, target - candidate, stack, res);
		stack.pop();
		//2️⃣改动二：回溯visited
		visited[i] = false;
	}
}

131.分割回文串

• 本题较难，大家先看视频来理解 分割问题，明天还会有一道分割问题，先打打基础。
• 题目链接：https://leetcode.cn/problems/palindrome-partitioning/
• 视频讲解：https://www.bilibili.com/video/BV1c54y1e7k6
• 文章链接：https://programmercarl.com/0131.%E5%88%86%E5%89%B2%E5%9B%9E%E6%96%87%E4%B8%B2.html

思路

例如对于字符串abcdef：

• 组合问题：选取一个a之后，在bcdef中再去选取第二个，选取b之后在cdef中再选取第三个…。
• 切割问题：切割一个a之后，在bcdef中再去切割第二段，切割b之后在cdef中再切割第三段…。

感受出来了不？

所以切割问题，也可以抽象为一棵树形结构，如图：

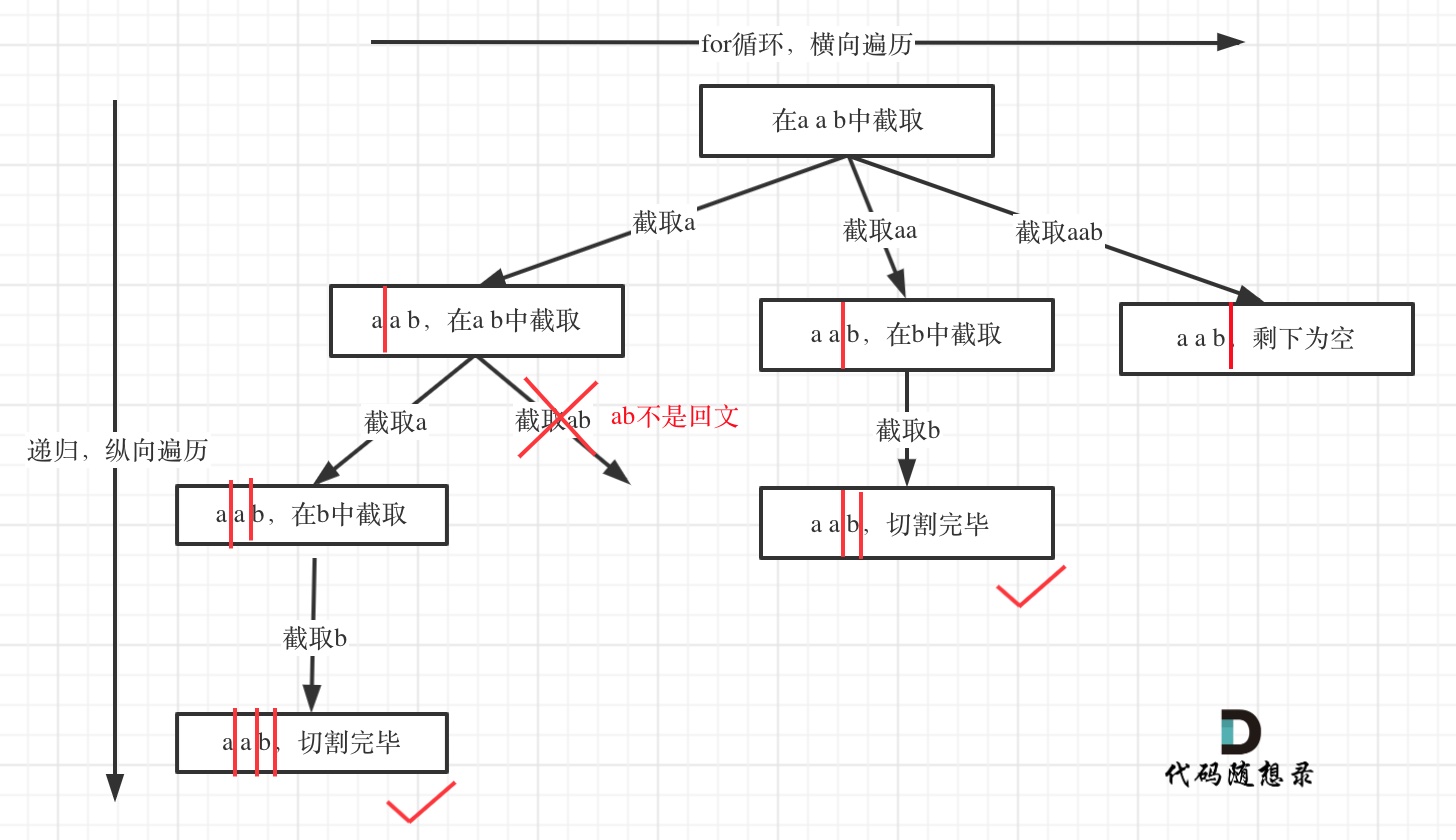
代码

注意必须按顺序输出所以用队列不能用栈

public class Day26_03_Leetcode_131 {
    public static void main(String[] args) {
        String s = "aab";
        System.out.println(partition(s));
    }
    static List<List<String>> res = new ArrayList<>();
    static Deque<String> path = new LinkedList<>();
    public static List<List<String>> partition(String s) {
        dfs(s, 0);
        return res;
    }
    //startIndex既表示从哪开始递归（类似组合问题），又是切割线
    public static void dfs(String s, int startIndex){
        if(startIndex == s.length()) {
            //把判断是否为回文的条件放到单层搜索的逻辑里，如果不是回文就不会进行递归，所以path都是回文
            res.add(new ArrayList<>(path));
            return;
        }
        //从startIndex开始遍历
        for (int i = startIndex; i < s.length(); i++) {
            //判断是否为回文串
            //(startIndex, i]就是切割出来的子串
            if(isPalindrome(s, startIndex, i)){
                //子串
                String str = s.substring(startIndex, i + 1);
                path.addLast(str);
                System.out.println(path);
            }else continue;
            dfs(s, i + 1);
            path.removeLast();
        }
        return;
    }
    //判断是否是回文串
    private static boolean isPalindrome(String s, int startIndex, int end) {
        for (int i = startIndex, j = end; i < j; i++, j--) {
            if (s.charAt(i) != s.charAt(j)) {
                return false;
            }
        }
        return true;
    }
}