有限元变分形式

最新推荐文章于 2024-10-24 15:56:04 发布

原创

最新推荐文章于 2024-10-24 15:56:04 发布 · 775 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#数学

本文探讨了在固体力学中的有限元方法，通过解析微分方程（adx^2d^2u + b = 0）来描述弹性杆的受力情况。利用最小化势能泛函Π来表述问题，并展示了使用线性及二次形函数作为插值基函数的过程，特别是在一个二次单元中如何构建形函数N1, N2, N3及其性质。" 74157470,348161,Docker容器网络配置：阻止特定IP访问,"['Docker网络', '网络安全', 'iptables规则', '容器隔离']

有如下的微分方程
$\begin{aligned} & a\frac{d^2u}{dx^2}+b=0, \quad 0 \leq x \leq 2L \\ & \left. u \right|_{x=0}=0 \\ & a\left. \frac{du}{dx} \right|_{x=2L}=R \end{aligned}$
其中 $a = E A$ ，该微分方程在固体力学中拥有具体的物理意义。它描述了由弹性模量为 $E$ 的材料制成的截面积为 $A$ 的一维杆，在右端承受分布载荷 $b$ 和集中载荷 $R$ 的张力，如图1.3所示。

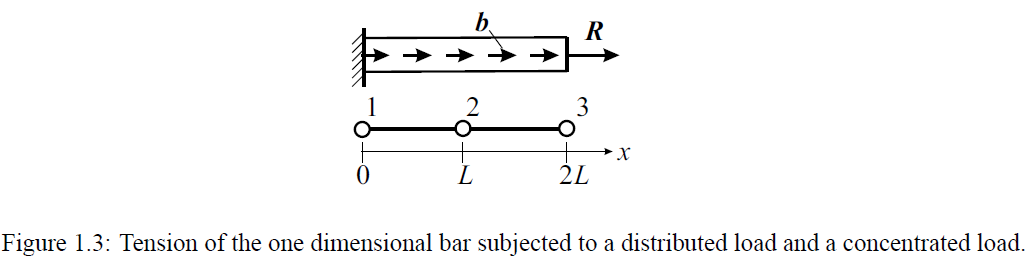
此问题可以用最小化势能泛函 $\Pi$ 来表示
$\begin{aligned} & \Pi=\int_L\frac{1}{2}a \left(\frac{du}{dx}\right)^2dx-\int_Lbudx-\left.Ru\right|_{x=2L}\\ & \left. u \right|_{x=0}=0 \end{aligned}$
我们同样使用上一节中使用的线性拉格朗日插值基函数来表示 ${u\}$ ，则可以写出第二个单元上的势能的值
$\begin{aligned} \Pi_{e} &=\int_{x_{1}}^{x_{2}} \frac{1}{2} a\{u\}^{T}\left[\frac{d N}{d x}\right]^{T}\left[\frac{d N}{d x}\right]\{u\} d x \\ &-\int_{x_{1}}^{x_{2}}\{u\}^{T}[N]^{T} b d x-\{u\}^{T}\left\{\begin{array}{c} 0 \\ R \end{array}\right\} \end{aligned}$