题解 P3195 【[HNOI2008]玩具装箱TOY】

斜率优化动态规划可以用来解决这道题。同时这也是一道经典的斜率优化基础题。

分析：明显是动态规划。令$dp[i]$为前$i$个装箱的最小花费。
转移方程如下：

$$dp[i]=\min\limits_{0 \leq j < i} \{ dp[j]+( \sum \limits_{k = j + 1}^{i}{C_k} + i - j - 1 - L) ^ 2\}$$

用$sum[i]$表示前$i$个容器的长度之和（即$C$的前缀和），方程简化为：

$$dp[i]=\min\limits_{0 \leq j < i} \{ dp[j]+( sum[i]-sum[j] + i - j - 1 - L) ^ 2\}$$

又令$f[i]$为$sum[i]+i$，继续简化方程为：

$$dp[i]=\min\limits_{0 \leq j < i} \{ dp[j]+( f[i]-f[j] - 1 - L) ^ 2\}$$

暴力dp是$O(n^2)$，考虑优化。如何优化，就是用前面所提到的斜率优化。这玩意到底是什么？我们先来继续对状态转移方程进行进一步的推导。

对于每个$dp[i]$可以知道都是由一个$j0$推过来的。这个$j0$对于当前的$i$是最优的决策。假设现在有两个决策$j_1,j_2 (1 \leq j_1 < j_2 < i)$，且决策$j_2$优于$j_1$，则有：

$$dp[j_1]+( f[i]-f[j_1] - 1 - L) ^ 2 \geq dp[j_2]+( f[i]-f[j_2] - 1 - L) ^ 2$$

拆开可得：

$$dp[j_1]+f[i]^2-2f[i](f[j_1]+1+L)+(f[j_1]+L+1)^2 \geq dp[j_2]+f[i]^2-2f[i](f[j_2]+1+L)+(f[j_2]+L+1)^2$$

化简可得：

$$2f[i](f[j_2] + 1 + L)-2f[i](f[j_1] + 1 + L) \geq dp[j_2]+(f[j_2]+1+L)^2 - (dp[j_1]+(f[j_1]+1+L)^2)$$

即：

$$2f[i] \geq \frac{dp[j_2]+(f[j_2]+1+L)^2 - (dp[j_1]+(f[j_1]+1+L)^2)}{f[j_2]-f[j_1]}$$
令$g[i] = (f[i]+L+1)^2$，可得：
$$2f[i] \geq \frac{dp[j_2]+g[j_2] - (dp[j_1]+g[j_1])}{f[j_2]-f[j_1]}$$

也就是说，若$j1,j2$满足上面这个式子，那么$j2$一定比$j1$优。

为什么叫斜率优化？因为上面这个式子可以把看作$dp[i]+g[i]$看做纵坐标，$f[i]$看做横坐标，上面的等式右侧就相当于$\frac{\Delta y}{\Delta x}=k$也就是一个一次函数的斜率。当这个斜率$k \leq 2f[i]$则$j_2$优于$j_1$。

假如我们有三个决策$j_1,j_2,j_3$（如下图）

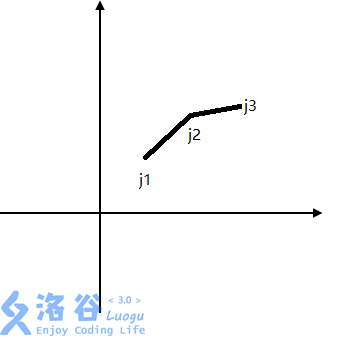
容易证明：$j_2$不可能是最优的。
这样一来，每两个决策间的斜率便是单调上升的。

所以有两种做法：

• 对于$dp[i]$，有了斜率单调上升这个条件，就可以去二分最优的决策点（也就是斜率小于$2f[i]$的）。复杂度$O(n \log n)$。
• 又因为$f[i]$是单调递增的，可以用单调队列来维护。具体实现就是，把决策放进一个单调队列里，如果队首和当前的$i$间的斜率 $<f[i]$，就把队首删掉（即h++）。对于队尾，就每次把加入$i$后不满足斜率单调上升的队尾全部删掉（即t–），最后把$i$放进单调队列就好了。

注意事项：
long long.
还有 $g[0]=(L + 1) ^ 2$而不是!!!!（因为这个我调了很久）

给一下单调队列做法的代码：

#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <algorithm>

using namespace std;

#define int long long
const int MAXN = 50050;
int N, L, dp[MAXN], sum[MAXN], f[MAXN], g[MAXN], h, t, Q[MAXN];

inline double xie(int j1, int j2)
{
    return (double) (dp[j2] + g[j2] - dp[j1] - g[j1]) / (f[j2] - f[j1]);
}
#undef int
int main()
{
    scanf("%d%d", &N, &L);
    for(int i = 1; i <= N; i++)
    {
        scanf("%d", &sum[i]);
        sum[i] += sum[i - 1];
        f[i] = sum[i] + i;
        g[i] = (f[i] + L + 1) * (f[i] + L + 1);
    }
    g[0] = (L + 1) * (L + 1); //important!!!
    for(int i = 1; i <= N; i++)
    {
        while(h < t && xie(Q[h], Q[h + 1]) <= 2 * f[i]) h++;
        dp[i] = dp[Q[h]] + (f[i] - f[Q[h]] - L - 1) * (f[i] - f[Q[h]] - L - 1); //更新dp值
        while(h < t && xie(Q[t], i) < xie(Q[t - 1], Q[t])) t--;
        Q[++t] = i;

    }
    printf("%lld\n", dp[N]);
    return 1；//防抄
}