数据降维-PCA算法（K-L变换）

转载
PCA（Principal Component Analysis，主成分分析）是一种常用的数据分析方法。PCA通过线性变换将原始数据变换为一组各维度线性无关的表示，可用于提取数据的主要特征分量，常用于高维数据的降维。

PCA主要步骤：

设有m条n维数据：
1）将原始数据按列组成n行m列矩阵X
2）将X的每一行（代表一个属性字段）进行零均值化，即减去这一行的均值
3）求出协方差矩阵

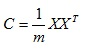
4）求出协方差矩阵的特征值及对应的特征向量，可以利用奇异值分解或样本协方差矩阵特征值分解（样本个数小于数据维度，即m<n）简化计算。
5）将特征向量按对应特征值大小从大到小按行排列成矩阵，取前k行组成矩阵P（或者取特征值总和的前95%特征值对应的特征向量），即保留大方差的特征（主对角线上的值对应该维特征的方差，），P为正交的低维线性子空间。
6）Y=PX即为降维到k维后的数据，Y表示X在P下的坐标，即X可由P线性组合而成，此时Y的协方差矩阵为对角矩阵，表明数据各维度间已去相关，通过人脸识别实验，得出人脸高维裸像素特征经过PCA降维后，同类之间明显聚类在一起，异类之间明显分开，所以通过最近邻分类法可以得到比较好的分类结果。