SDU程序设计思维与实践作业Week10

最新推荐文章于 2025-12-22 09:47:08 发布

原创最新推荐文章于 2025-12-22 09:47:08 发布 · 445 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #动态规划

SDU程序设计思维与实践作业Week10

A签到题
BLIS & LCS
C

A签到题

题目

input&&output

Sample

    #Simple Input 1
    120 51840
    #Simple Output 1
    7
    #Simple Input 2
    42 42
    #Simple Output 2
    0
    #Simple Input 3
    48 72
    #Simple Output 3
    -1

题解

本题直接暴力就可以了

C++代码

#include<iostream>
#include<cmath>

using namespace std;

int main(){
	int n,m;
	cin>>n>>m;
	if(m%n != 0) cout<<"-1"<<endl;
	else{
		int k=m/n;
		int num=0;
		while(k%2==0) {
			k/=2;
			num++;
		}
		while(k%3==0){
			k/=3;
			num++;
		}
		if(k == 1) cout<<num<<endl;
		else cout<<"-1"<<endl;
	}
	return 0;
}

BLIS & LCS

题目

input&&output

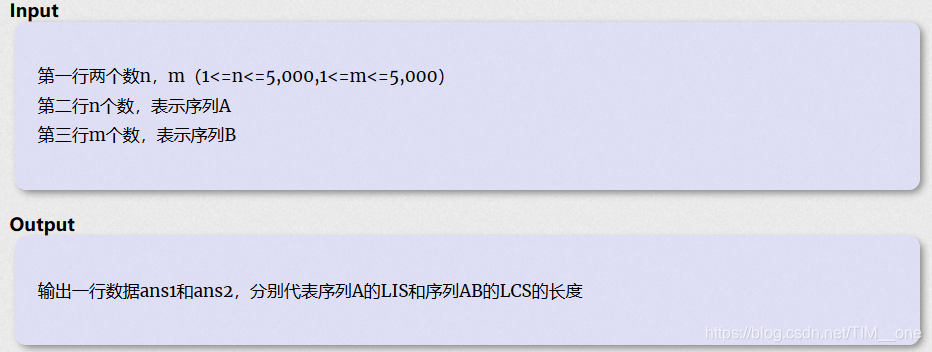
Sample

#input：
5 5
1 3 2 5 4
2 4 3 1 5
#output：
3 2

题解

1.LIS：最长上升子序列（严格递增）
	我们只需要记录0~i的最长上升子序列就可以了
	计算i+1时  若 存在j<i+1 那么我们就将他的标记矩阵（arr）即为max（arr[j]）
	最后再假设i+1本身
2.LCS：最长公共子序列
	起初我想到将LCS转化为LIS（我们只要记录 A的元素在B中出现的位置然后求LIS就可以了，后来发现这种直接转化的方法对于A的元素在B中多次出现不太好处理（需要全部记录然后寻找最大LIS，因此换用另一种方法）
	由于涉及到两个数组并且索引位置各不相同，一维不足以记录变化状态，因此我们采用二维数组作为标记矩阵，f[i][j] 标识 Ai、Bj之前最长公共子序列，那么判断 i+1或j+1时若相同则为f[i][j]+1、不同此时有两种种情况 f[i][j-1]、f[i-1][j]由于ij位置不可放因此为二者的最大值，最终LCS即为f[m][n] （A大小为m B为m）

C++代码

#include<iostream>

using namespace std;
const int maxn = 1e4;
long long A[maxn],B[maxn];
long long mark[maxn];
long long C[maxn][maxn];//存储 A中元素在B中出现的位置

void init(int n,long long * arr){
	for(int i=0;i<n;i++) arr[i] = 0;
}
void LIS(int n,long long *arr){
	//最长上升子序列  严格递增
	for(int i=0;i<n;i++){
		for(int j=0;j<i;j++)
			if(arr[j] < arr[i] && mark[j] > mark[i])
				mark[i] = mark[j];		
		mark[i]++;
	} 
}

void LCS(int n,int m){
	for(int i=0;i<n;i++)
		for(int j=0;j<m;j++)
			C[i][j] = 0;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++){
			if(A[i-1] == B[j-1]) C[i][j] = C[i-1][j-1] + 1;
			else C[i][j] = max(C[i][j-1],C[i-1][j]);
		}
} 
int main(){
	int m,n;
	long long ma=0;
	cin>>n>>m;
	init(n,A);
	init(m,B);
	init(n,mark);
	for(int i=0;i<n;i++) cin>>A[i];
	for(int i = 0;i<m;i++) cin>>B[i];
	LIS(n,A);
	for(int i=0;i<n;i++) if(mark[i]>ma) ma = mark[i];
	cout<<ma<<" ";
	init(n,mark);
	LCS(n,m);
	cout<<C[n][m]<<endl;
	return 0;
}

C

题目

input&&output

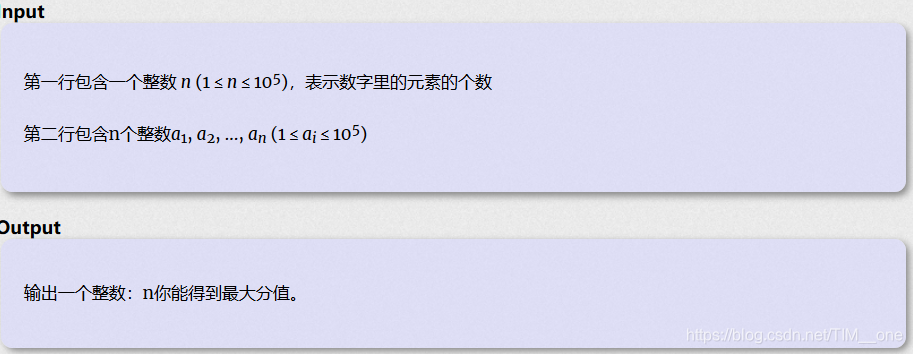
Sample

    #Input
    2
    1 2
    #Output
    2
    #Input
    3
    1 2 3
    #Output
    4
    #Input
    9
    1 2 1 3 2 2 2 2 3
    #Output
    10

题解

这是一道拿数问题的变种（DP解决）
实际上仅仅是吧每个数的个数增加了，因此我们更新时增加的数不再是数字本身而是数字*个数
拿数问题：
	要从一组数中拿数，但拿完之后x-1、x+1均不可取，我们构建dp[i]为i拿数后的最大值，那么i+1如何取，i+1有两种可能，若i被取了那么i+1不可取，若i-1被取了那么i可取那么dp[i]为二者的较大值（只不过此处若取i增加的数量为  x*num_x

C++代码

#include<iostream>

using namespace std;

const int maxn = 1e6+500;
long long num[maxn],dp[maxn],ele[maxn];
long long mx = -1,mn = maxn,curr;
int main(){
	int n;
	cin>>n;
	for(int i=0;i<n+1;i++) {num[i] = 0;dp[i] = 0;ele[i]=0;}
	for(int i=0;i<n;i++){
		cin>>curr;
		mx = max(mx,curr);
		mn = min(mn,curr);
		num[curr]++;
	}

	for(int i=mn;i<=mx;i++)
		if(i==mn) dp[i] = i*num[i];
		else if(i==mn+1) dp[i] = max(dp[i-1],i*num[i]);
		else dp[i] = max(dp[i-1],dp[i-2] + i*num[i]);
	cout<<dp[mx]<<endl;
	return 0;
}