[论文笔记] Handling Information Loss of Graph Neural Networks for Session-based Recommendation

原文地址
KDD 2020 | Handling Information Loss of Graph Neural Networks for Session-based Recommendation

Handling Information Loss of Graph Neural Networks for Session-based Recommendation (github.com)

最近，图神经网络（GNN）因其在各种应用中令人信服的性能而越来越受欢迎。许多先前的研究也尝试将 GNN 应用于基于会话的推荐并获得了可喜的结果。然而，这些基于 GNN 的基于会话的推荐方法存在两个信息丢失问题：

1. 有损会话编码问题

   由于从会话到图的有损编码以及消息传递期间的置换不变聚合，一些关于物品转换的顺序信息被忽略。

   提出了一种无损编码方案和一个基于 GRU 的边缘顺序保留聚合层，专门设计用于处理无损编码的图。

2. 无效的远程依赖捕获问题

   由于层数有限，无法捕获会话中的某些远程依赖项。

   提出了一个快捷图注意层，它通过沿着快捷连接传播信息来有效地捕获远程依赖关系。

通过结合这两种层，能够构建一个没有信息丢失问题的模型，并且在三个公共数据集上的表现优于最先进的模型。提出了一种新的 GNN 模型，称为 LESSR（基于会话的推荐的无损边序保留聚合和快捷图注意）。

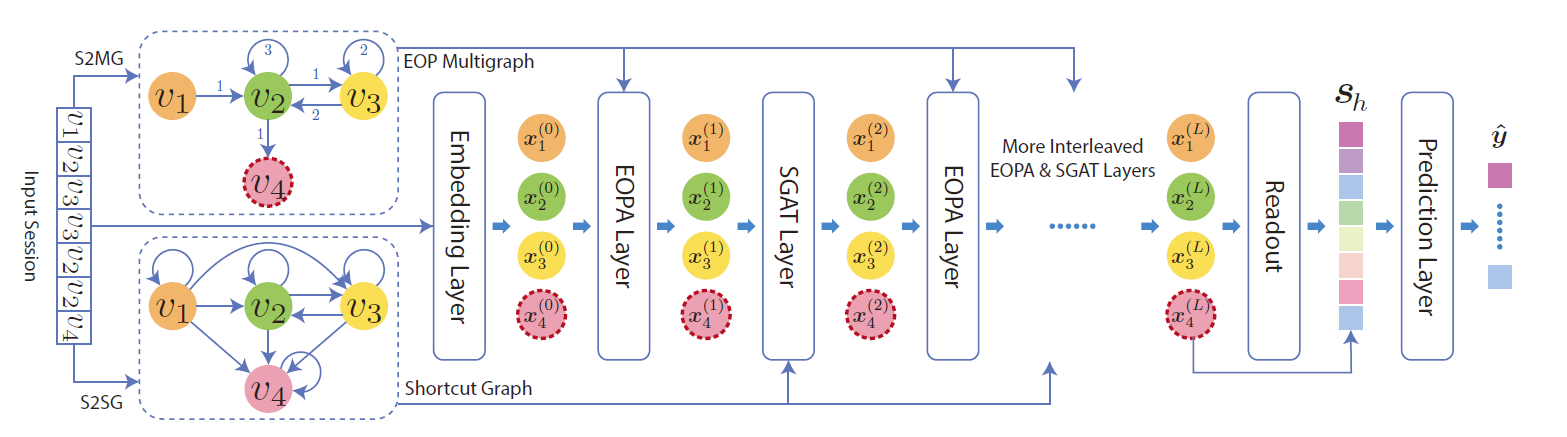
图2说明了 LESSR 的工作流程。 给定的输入会话首先被转换为称为边序保留 (EOP) 多重图的无损编码图和快捷图，其中 EOP 多重图可以解决有损会话编码问题，快捷图可以解决无效的远程依赖捕获问题 . 然后，将图与物品嵌入一起传递到多个边序保留聚合 (EOPA) 和快捷图注意 (SGAT) 层以生成所有节点的潜在特征。 EOPA 层使用 EOP 多重图捕获本地上下文信息，SGAT 层使用快捷图有效地捕获远程依赖关系。 然后，应用带有注意力的读出函数从所有节点嵌入生成图级嵌入。 最后，我们将图级嵌入与用户最近的兴趣相结合来提出建议。

1. GNN

GNN 是直接对图数据进行操作的神经网络。 它们用于学习任务，例如图分类、节点分类和链接预测问题。 在本文中，只关注图分类问题，因为基于会话的推荐可以表述为这样的问题。

令$G=(V,E)$为给定的图，$V,E$分别代表节点集和边集，每个节点$i\in V$与一个节点特征向量$x_i$相连，该特征向量会传递给GNN的第一层作为初始的节点表示。大多数 GNN 可以从消息传递的角度来理解。 在 GNN 的每一层中，节点表示通过沿边传递消息来更新。 该过程可以表述如下：

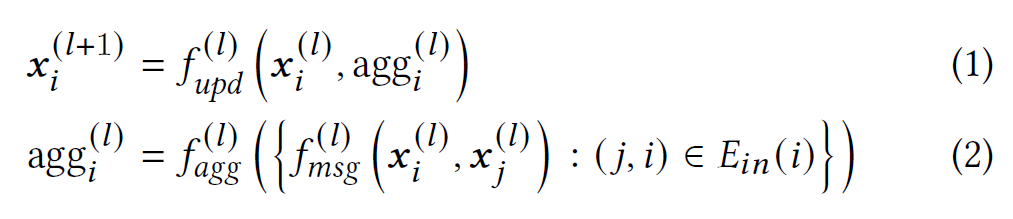
符号	表示	解释
$x_i^{(l)}$	节点$i$在第$l$层的表示
$E_{in}(i)$	节点$i$的传入边的集合
$f_{msg}^{(l)}$	信息函数	计算要从相邻节点传播到目标节点的消息
$f_{agg}^{(l)}$	聚合函数	聚合传递给目标节点的信息
$f_{upd}^{(l)}$	更新函数	根据原始节点表示和聚合信息计算新节点表示

令$L$为 GNN 中的层数。 在$L$层的$L$步消息传递之后，最终的节点表示捕获了有关图结构和$L$跳邻域内节点特征的信息。 对于图分类任务，读出函数$f_{out}$用于通过聚合最后一层中所有节点的表示来生成图级别表示$h_G$：

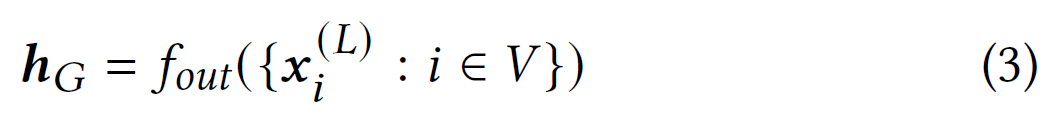
2. 论文模型

提出的方法涉及两个主要组成部分：

1. 将每个输入会话转换为边序保留 (EOP) 多图和快捷图的模块，因为 GNN 模型需要两种类型的图作为输入（第 2.2 节）；
2. 提出的 GNN 模型 LESSR（第 2.3 节）。

2.1 问题定义

基于会话的推荐是next-item推荐的一个例子。 它的目标是在给定活动会话中已经点击的一系列物品的情况下推荐用户最有可能点击的物品。给定通用物品集合 I = { v 1 , v 2 , . . . , v ∣ I ∣ } I=\lbrace v_{1},v_{2},...,v_{|I|}\rbrace I={ v1​,v2​,...,v